- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
AQA A Level Maths: Pure复习笔记9.1.2 Parametric Equations - Eliminating the Parameter
Parametric Equations - Eliminating the Parameter
What does eliminating the parameter mean?
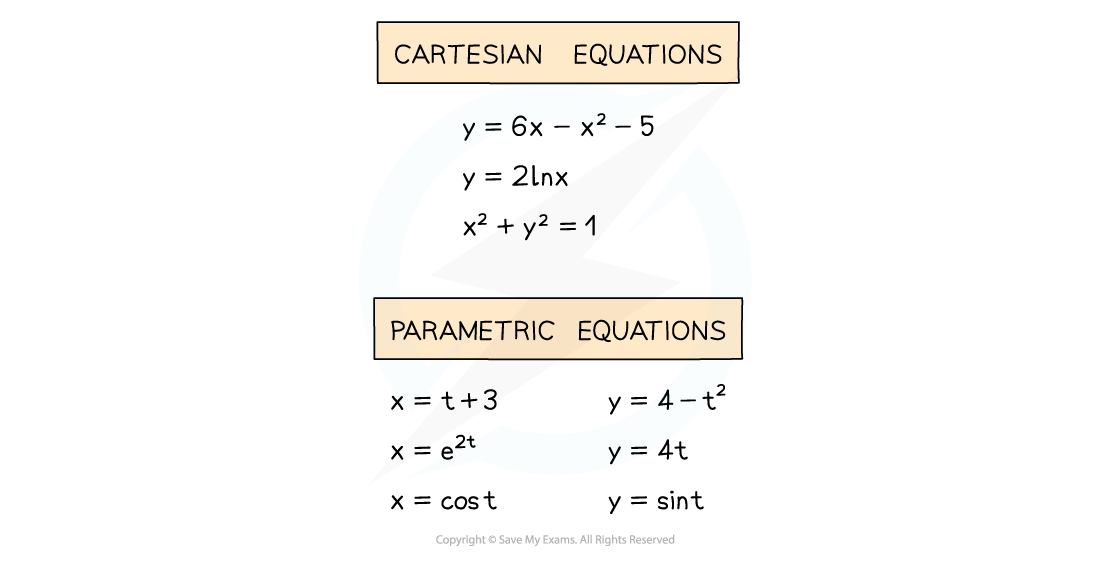
- In parametric equations, x = f(t) and y = g(t)
- There is still a connection directly linking x and y
- This will be the Cartesian equation of the graph
How do I find the Cartesian equation from parametric equations?
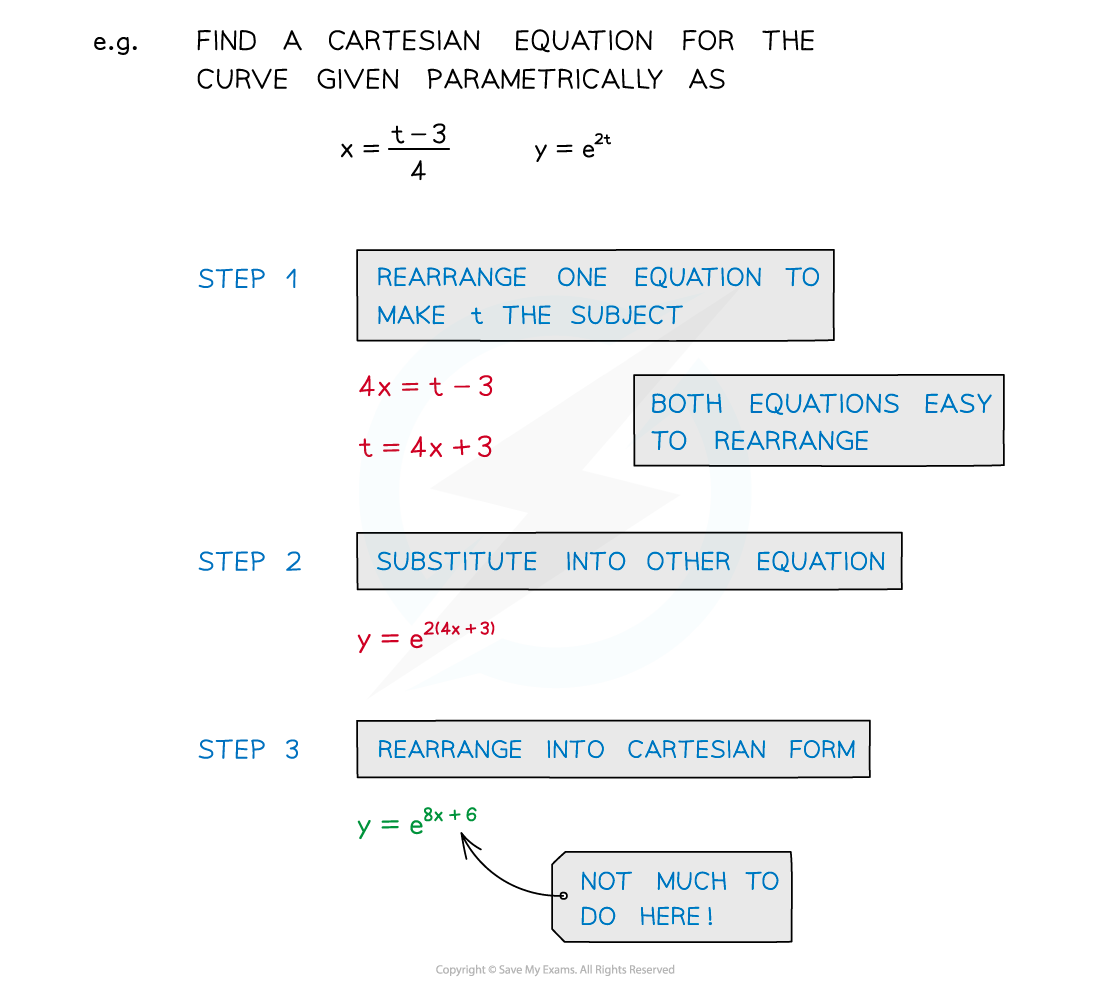
- STEP 1: Rearrange one of the equations to make t the subject
- Either t = p(x) or t = q(y)
- STEP 2: Substitute into the other equation
- STEP 3 Rearrange into the desired (Cartesian) form
How do I eliminate t when trig is involved?

- STEP 1 Rearrange both equations into the forms “cos t = …” and “sin t = …”
- STEP 2 Square BOTH sides of BOTH equations
- STEP 3 Add the equations together
- STEP 4 The trig identity “sin2 x + cos2 x ≡ 1” eliminates t
- STEP 5 Rearrange into desired (Cartesian) form
- This technique is seen in Trigonometric Identities
Exam Tip
When choosing which equation to rearrange, aim for “as simple as possible”:
- Linear equations are simpler than quadratics
- eg Rearrange x = 2t + 3or
y = 3t2 +3t -4 ?
- eg Rearrange x = 2t + 3or
- Single exponential terms are quite easy to deal with
- eg x = et → t = ln x
Trig identities may be needed and remember squared terms are good!
- eg sin2 x + cos2 x ≡ 1
Worked Example

转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





