- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
AQA A Level Maths: Pure复习笔记8.2.1 Integration as the limit of a sum
Integration as the limit of a sum
Finding the area under a curve
- Definite integration allows us to find the area under a curve
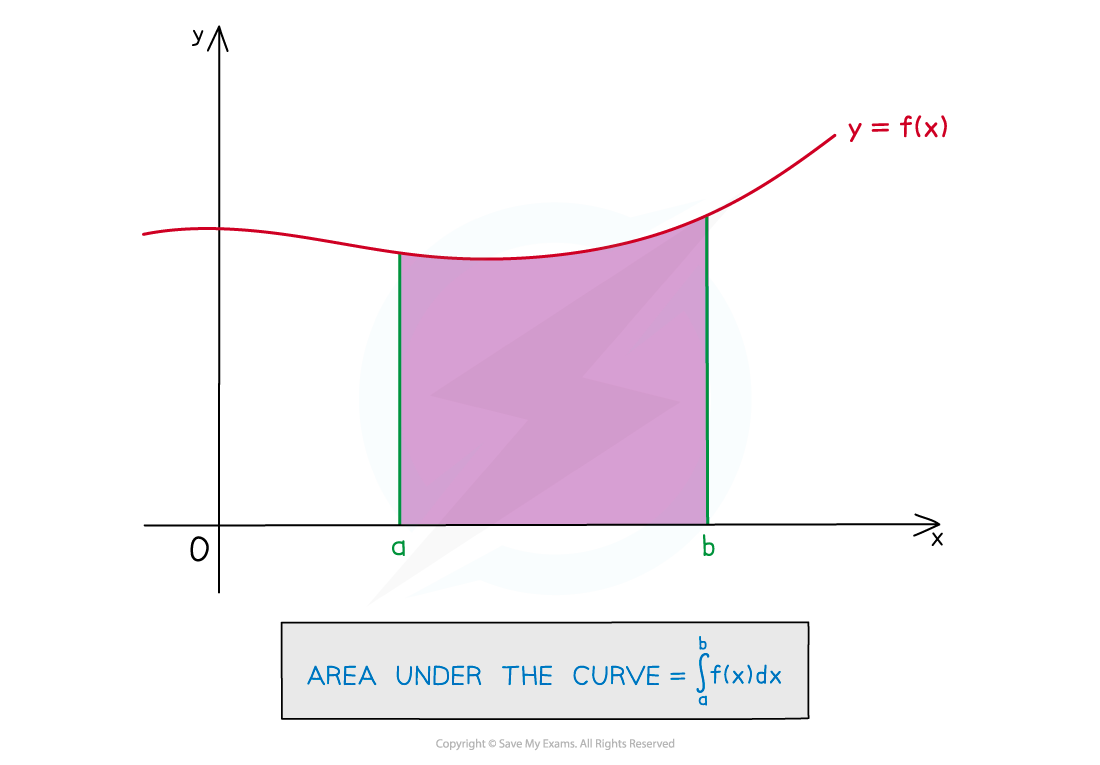
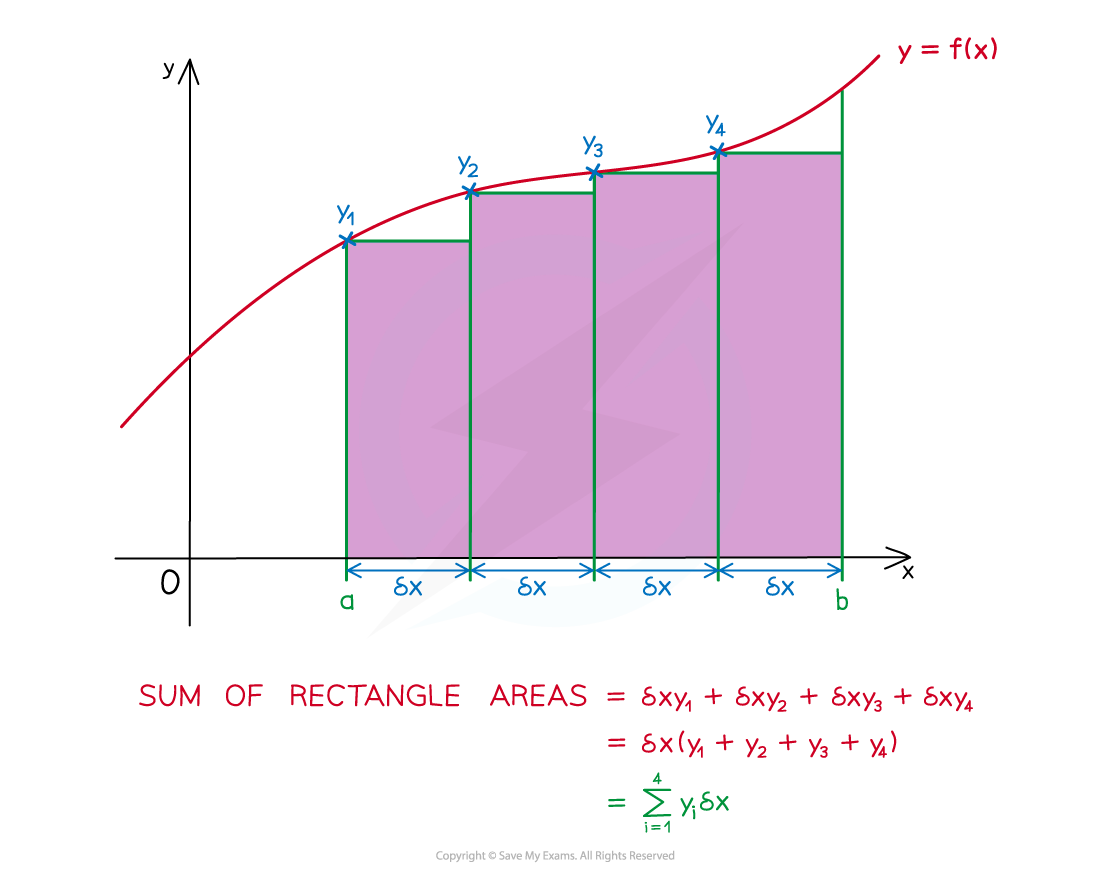
- An estimate for the area under the curve is the sum of the rectangular areas
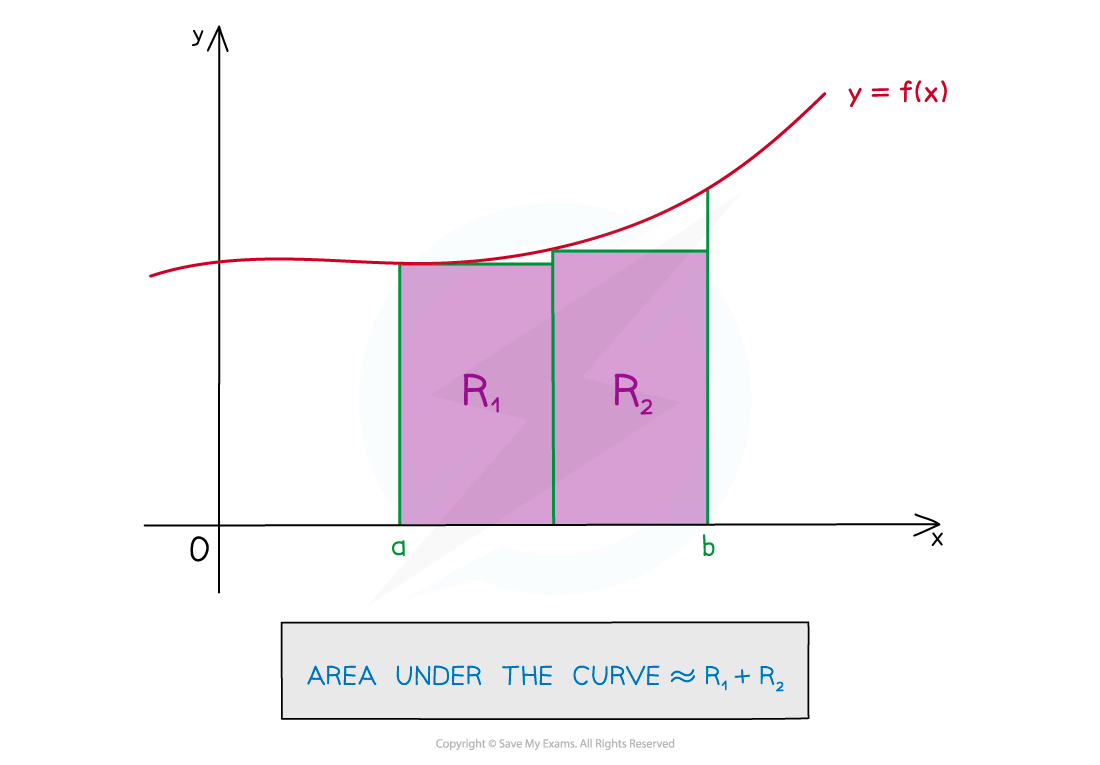
- If the number of rectangles increases and their width decreases, the estimate is more accurate
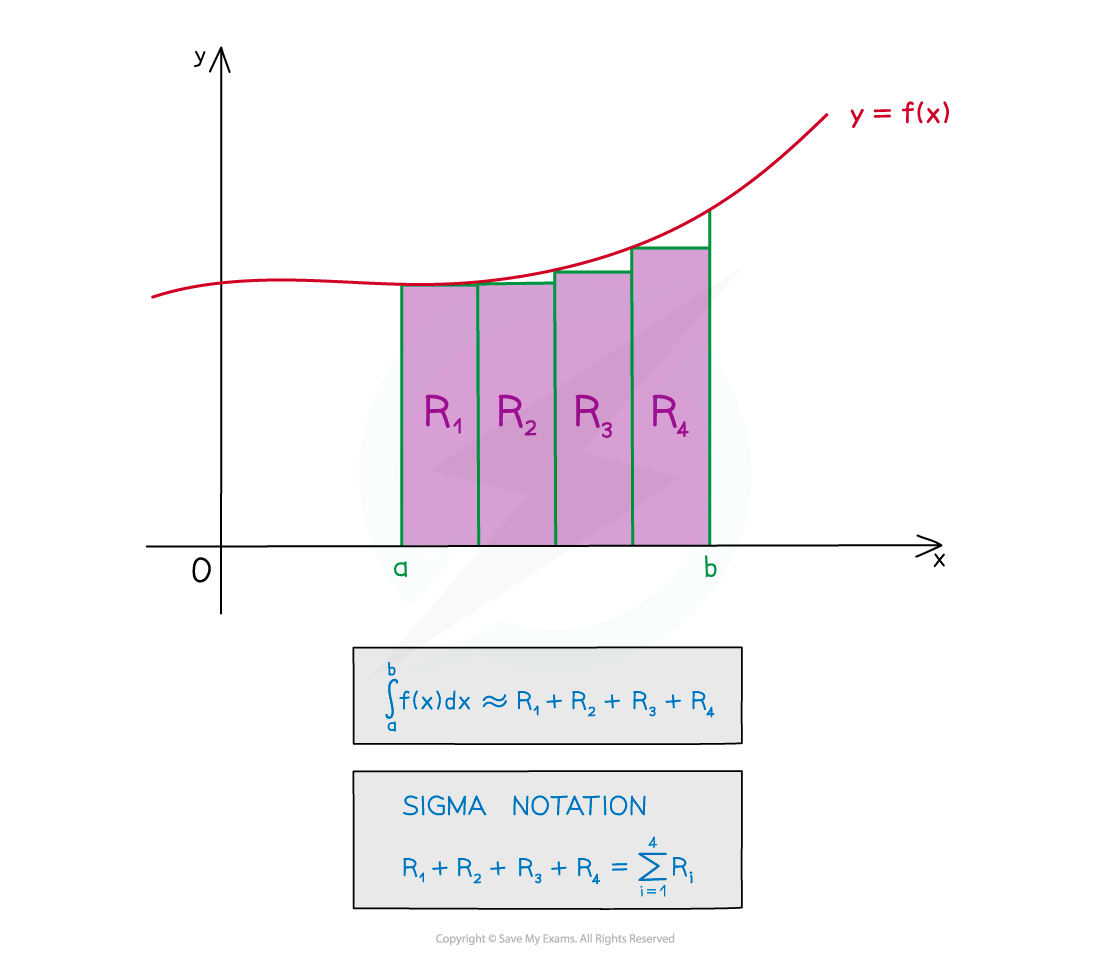
- The sum of the rectangle areas will have a limit, however small they get
- The sum will become closer and closer to the area under the curve
- This is called the limit of the sum
What is integration as the limit of a sum?
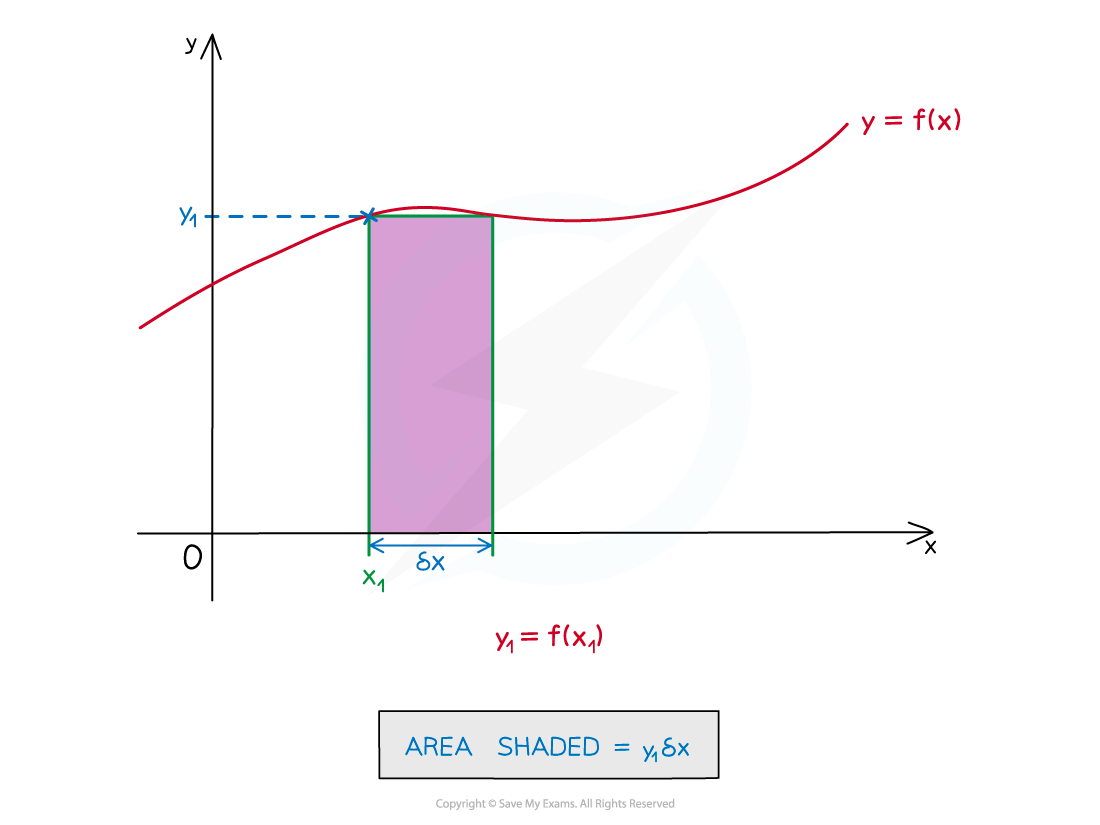
- The width of a rectangle can be considered as a small increase along the x-axis
- This is denoted by δx
- The height (length) will be the y-coordinate at x1 – ie f(x1) (rather than f(x1+δx))
- If we use four of these small rectangles between a and b we get
- As more rectangles are used …
- … δx gets smaller and smaller, ie δx → 0
- … n, the number of rectangles, gets bigger and bigger, ie n → ∞
- … the sum of the area of the rectangles becomes closer to the area under the curve
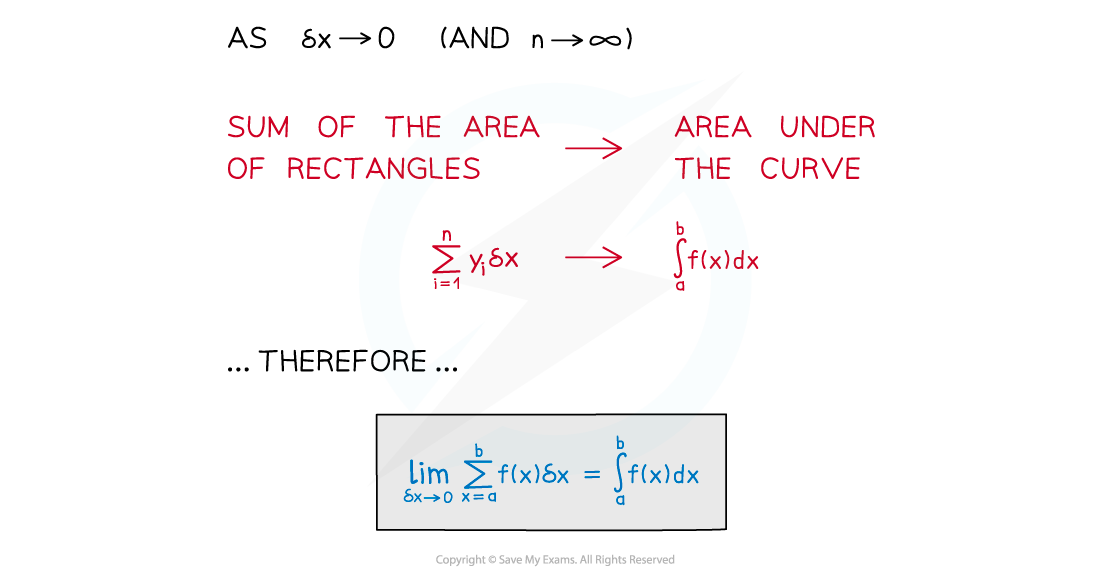
- This is the meaning of integration as the limit of a sum
How do questions use integration as the limit of a sum?
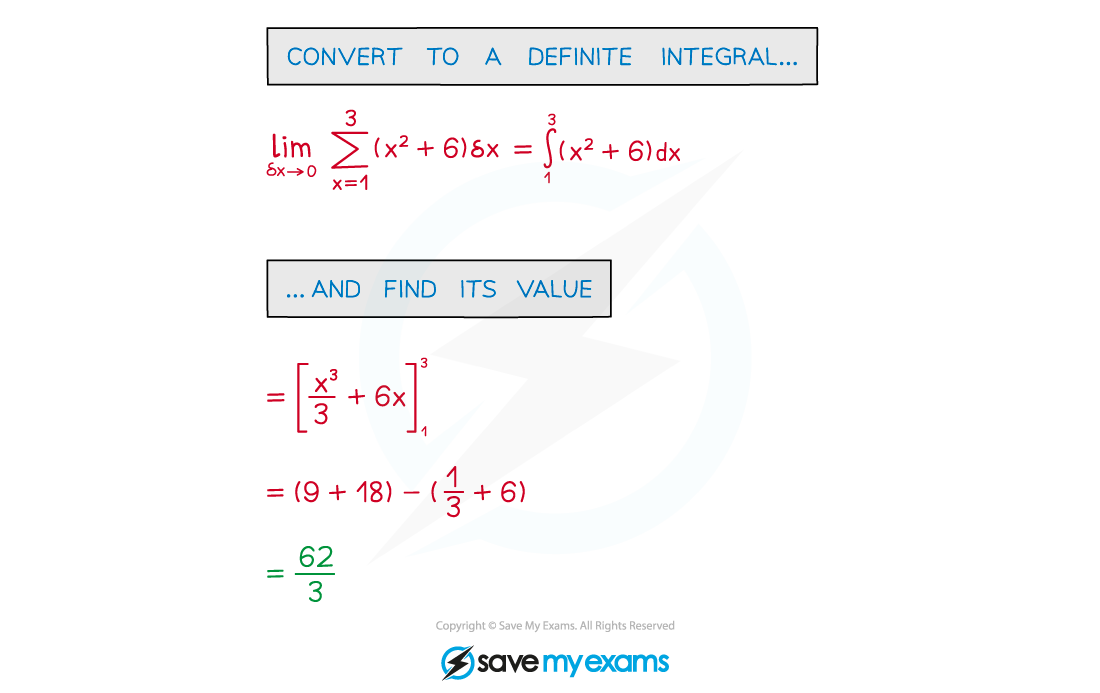
- STEP 1 Recognise the notation
- STEP 2 Convert to a definite integral
- STEP 3 Find the value of the integral
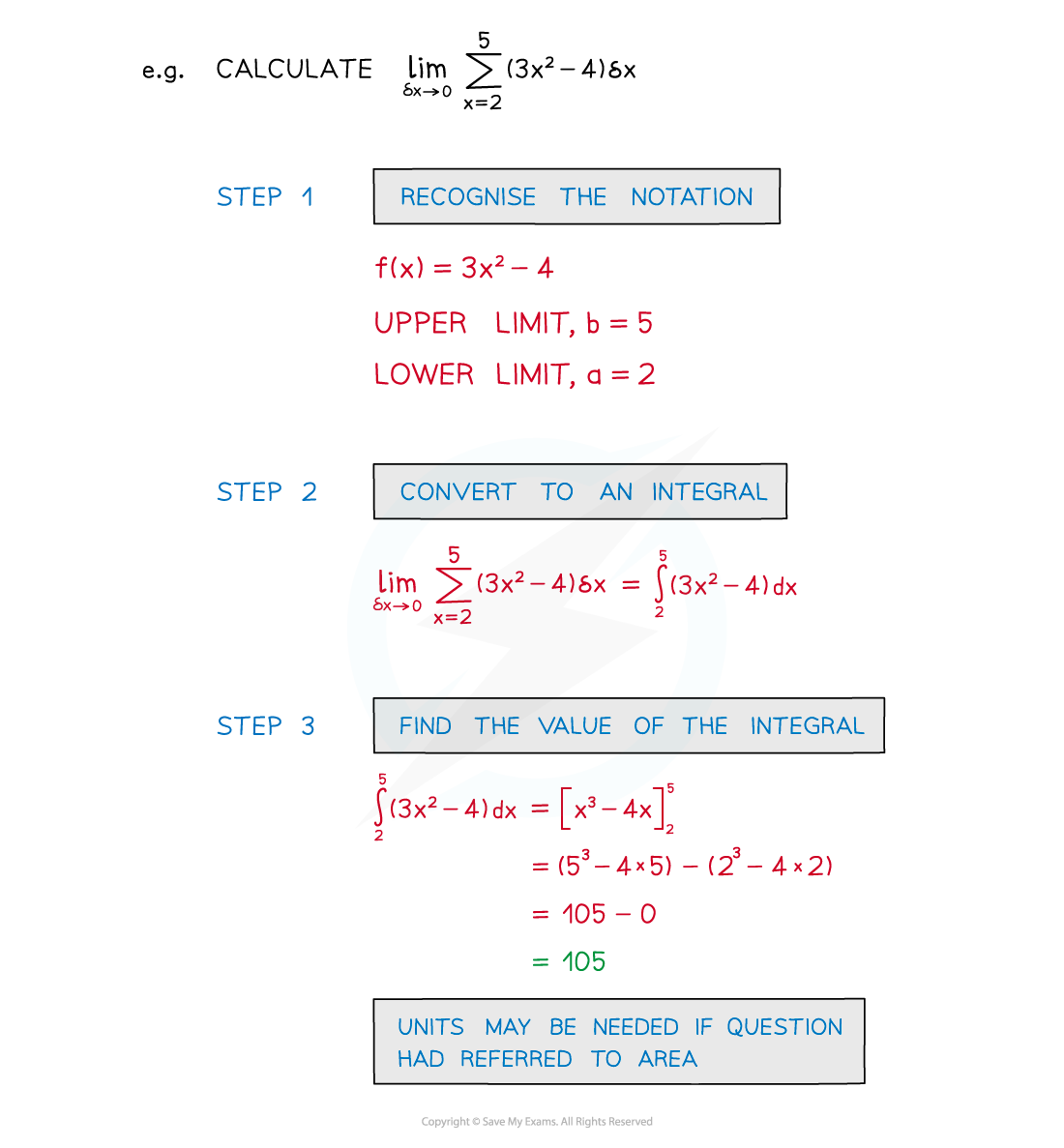
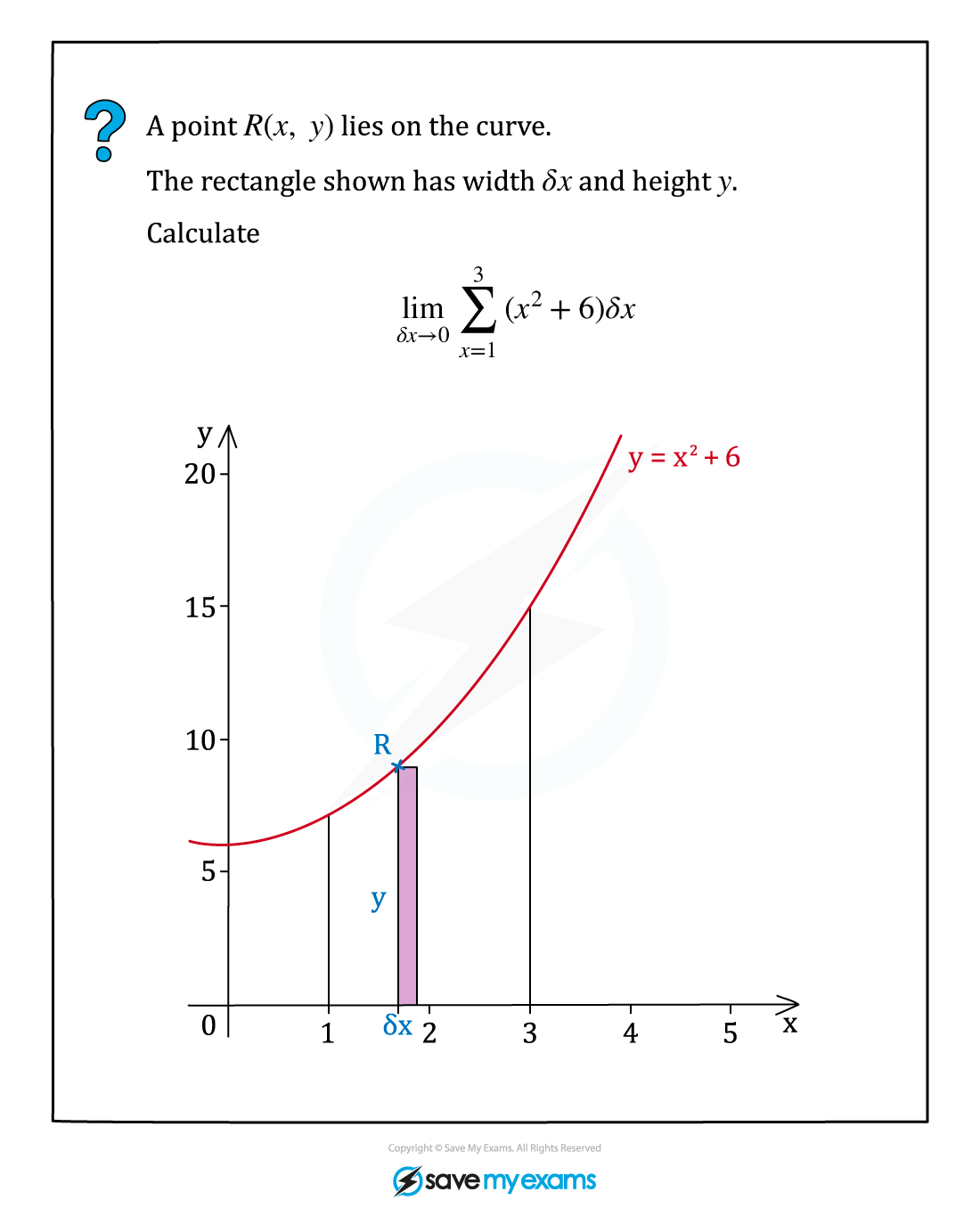
Worked Example
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





