- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
AQA A Level Maths: Pure复习笔记6.1.2 Logarithmic Functions
Logarithmic Functions
Logarithmic functions
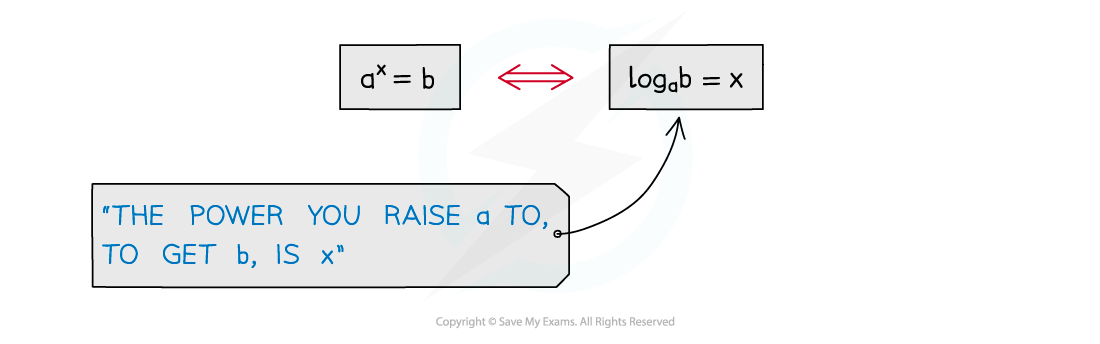
- a = bx and log b a = x are equivalent statements
- a > 0
- b is called the base
- Every time you write a logarithm statement say to yourself what it means
- log3 81 = 4“the power you raise 3 to, to get 81, is 4”
- logp q = r“the power you raise p to, to get q, is r”
Logarithm rules
- A logarithm is the inverse of raising to a power so we can use rules to simplify logarithmic functions
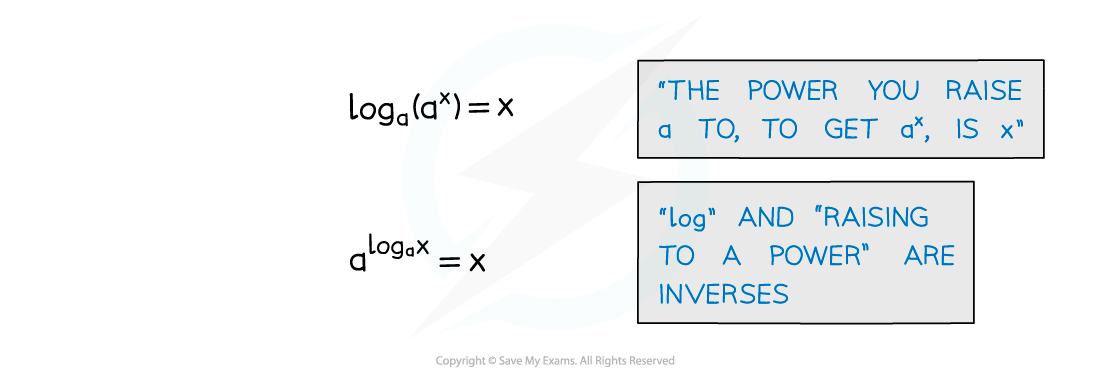
- There are more laws of logarithms but these are the only ones needed for A level
How do I use logarithms?
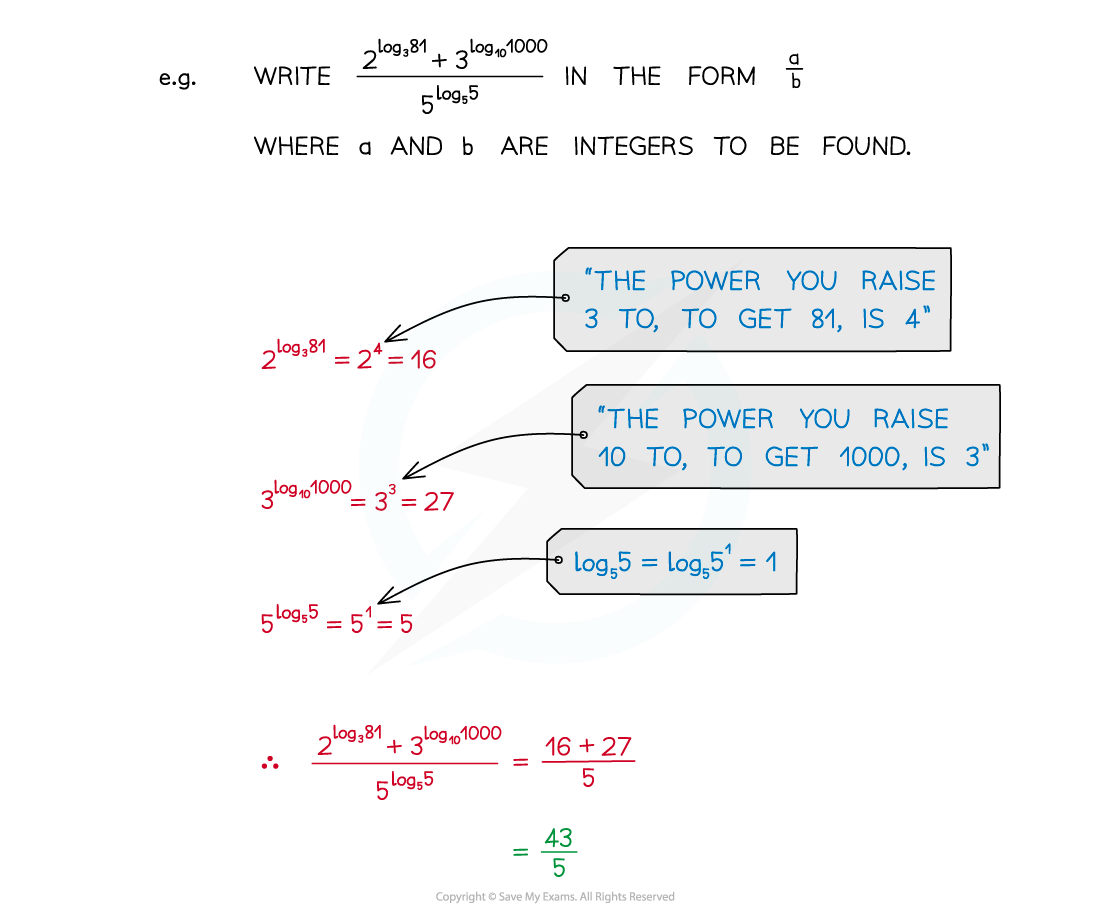
- Recognising the rules of logarithms allows expressions to be simplified
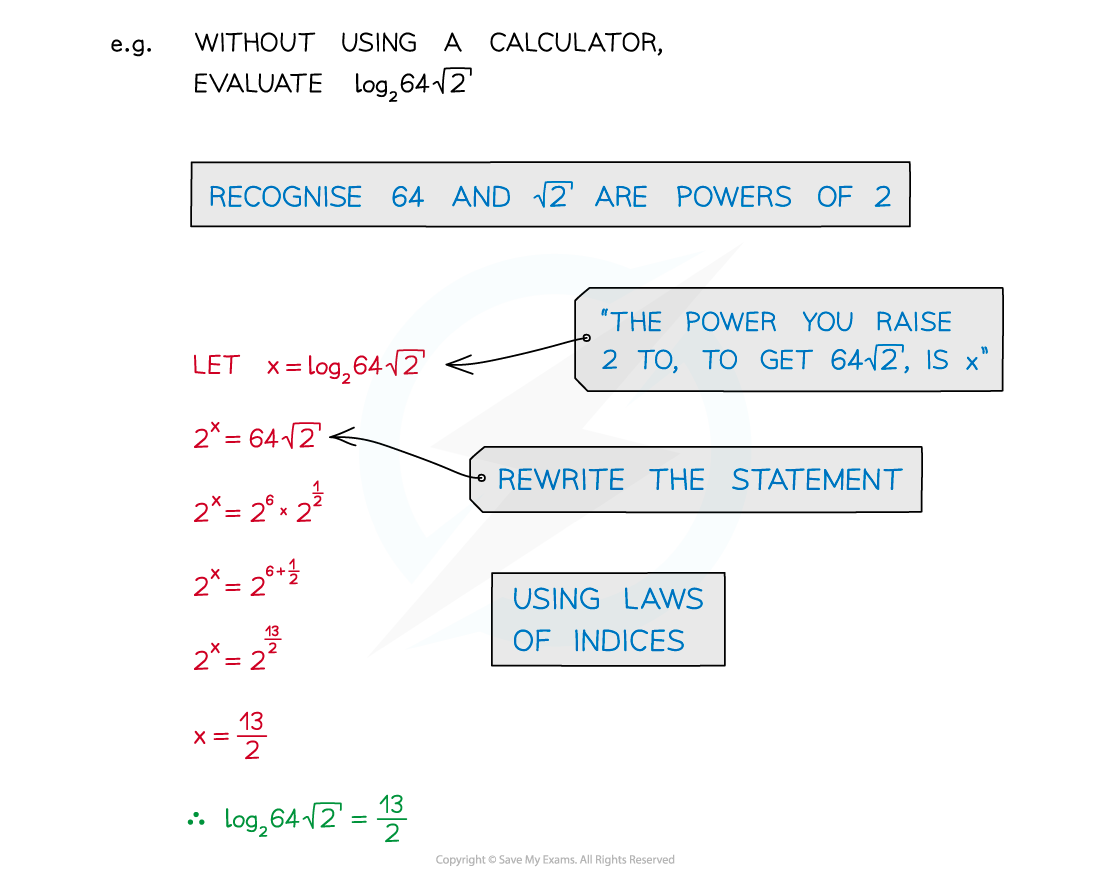
- Recognition of common powers helps in simple cases
- Powers of 2: 20 = 1, 21 = 2, 22 = 4, 23 = 8, 24 =16, …
- Powers of 3: 30 = 1, 31 = 3, 32 = 9, 33 = 27, 34 = 81, …
- The first few powers of 4, 5 and 10 should also be familiar
For more awkward cases a calculator is needed
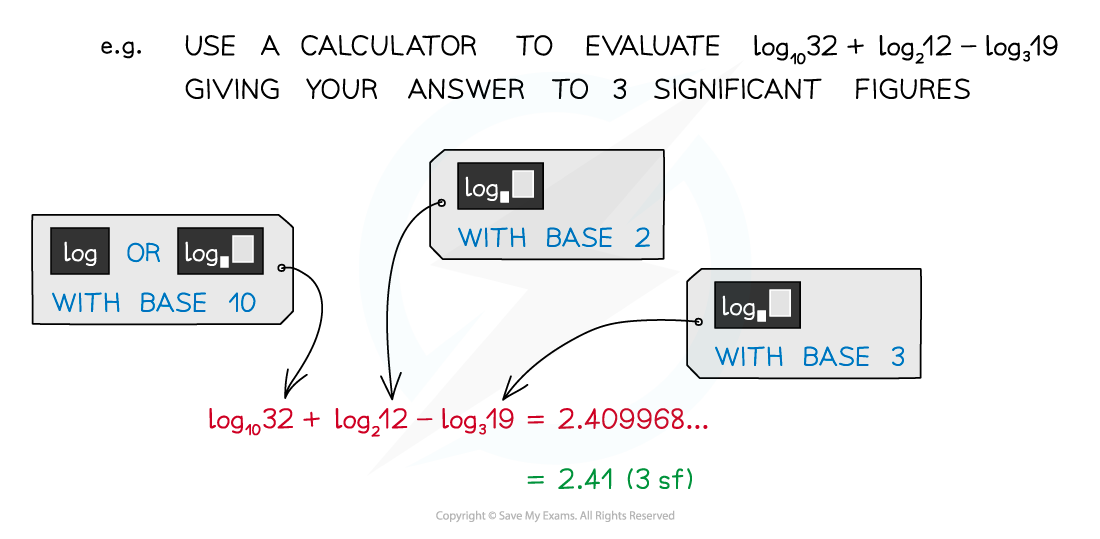
- Calculators can have, possibly, three different logarithm buttons

- This button allows you to type in any number for the base

- Natural logarithms (see “e”)

- Shortcut for base 10 although SHIFT button needed
- Before calculators, logarithmic values had to be looked up in printed tables
Notation
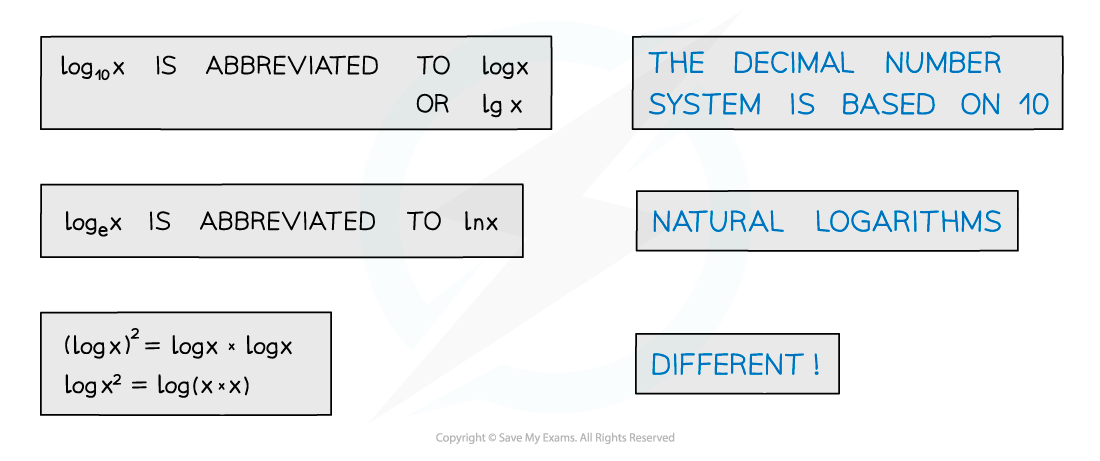
- 10 is a common base
- log10 x is abbreviated to log x or lg x
- The value e is another common base
- loge x is abbreviated to ln x
- (log x)2 ≠ log x2
Worked Example
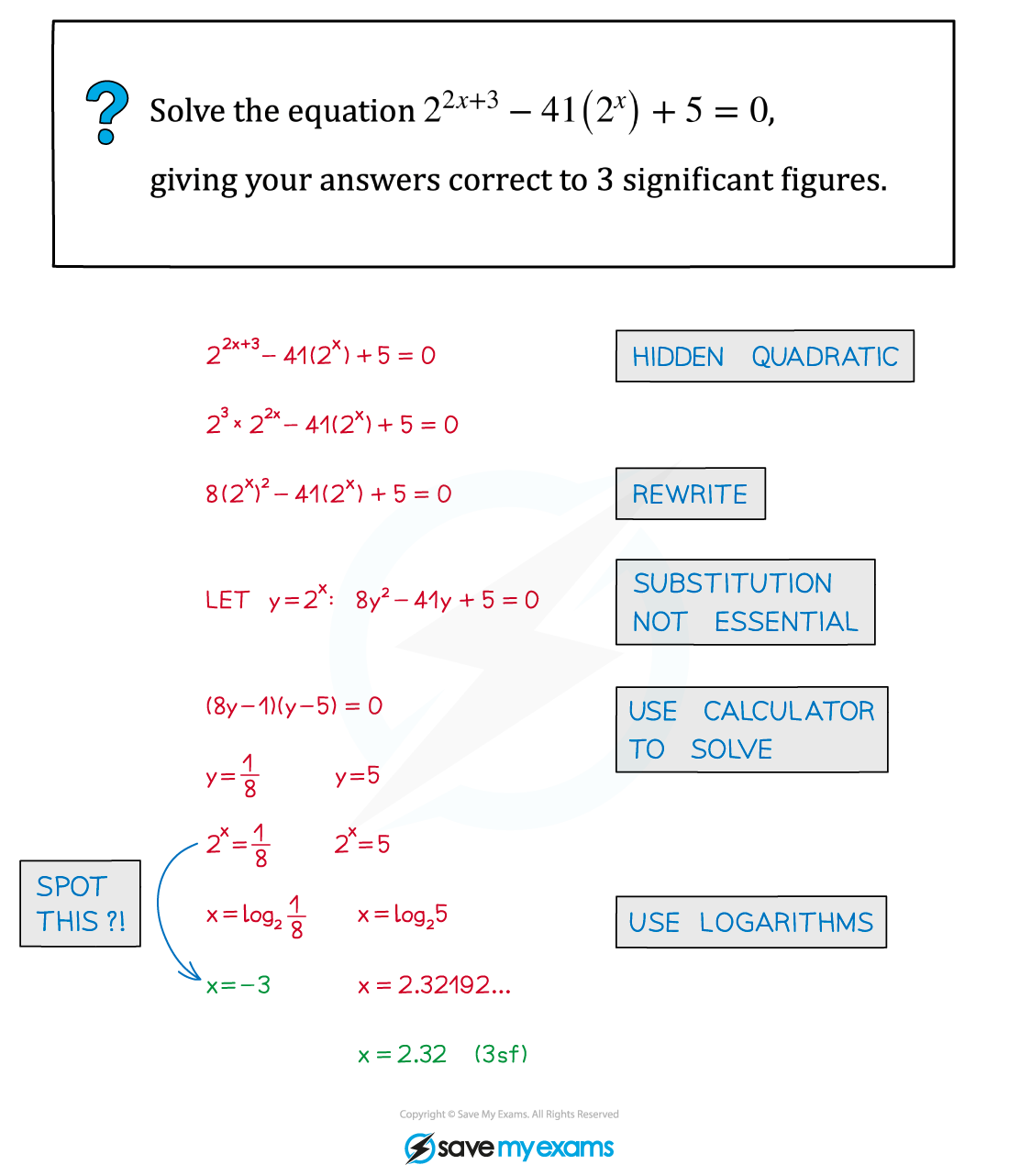
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





