- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
AQA A Level Maths: Pure复习笔记5.5.4 Inverse Trig Functions
Inverse Trig Functions
What are arcsin, arccos and arctan?
- These functions are the inverse functions of sin, cos and tan
- sin (arcsin x) = x
- cos (arccos x) = x
- tan (arctan x) = x
- The domains of sin, cos, and tan must first be restricted to make them one-to-one functions (only one-to-one functions have inverses)
What are the restricted domains?
- domain of sin x is restricted to -π/2 ≤ x ≤ π/2 (-90° ≤ x ≤ 90°)
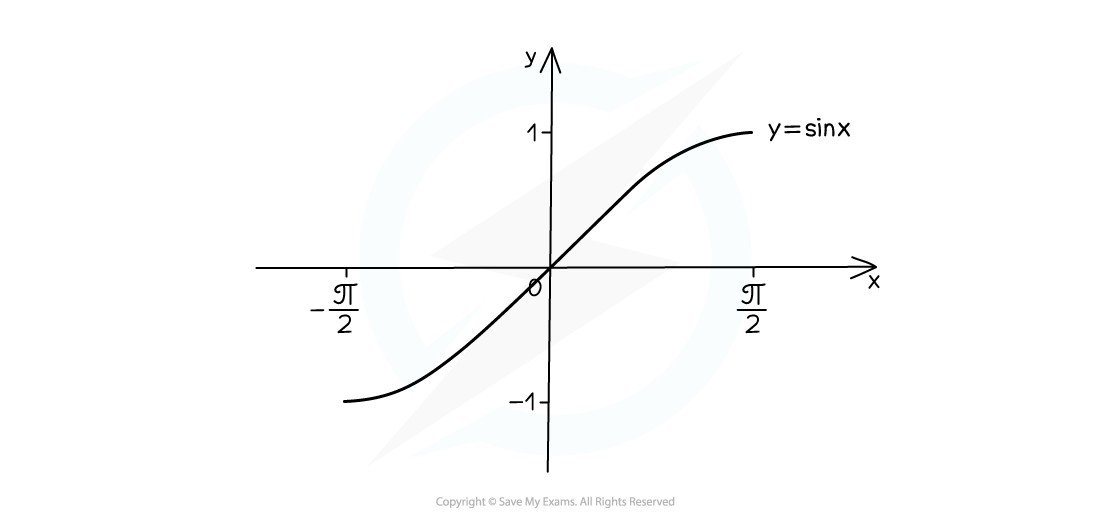
- domain of cos x is restricted to 0 ≤ x ≤ π (0° ≤ x ≤ 180°)
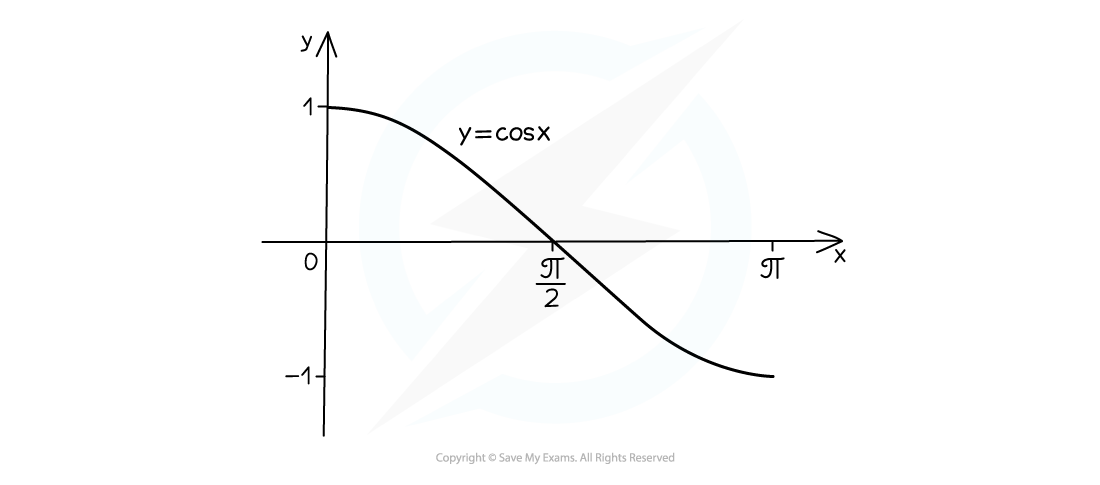
- domain of tan x is restricted to -π/2 < x < π/2 (-90° < x < 90°)

What does the graph of arcsin look like?
- The graph of y = arcsin x looks like this:
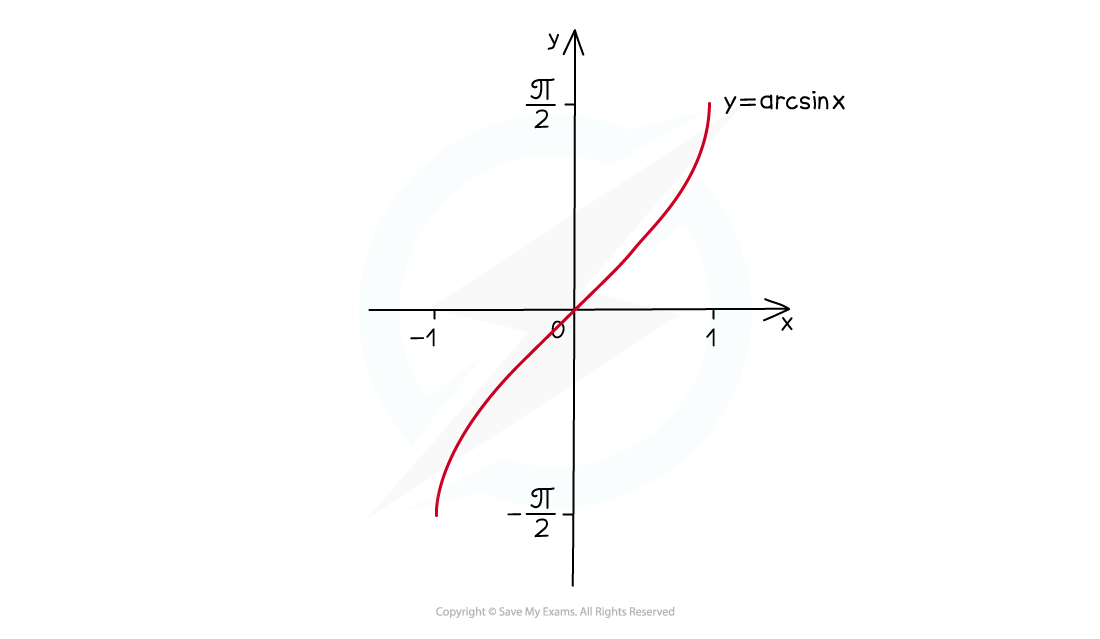
- the domain is -1 ≤ x ≤ 1
- the range is -π/2 ≤ arcsin x≤ π/2 (-90° ≤ arcsin x ≤ 90°)
What does the graph of arccos look like?
- The graph of y = arccos x looks like this:
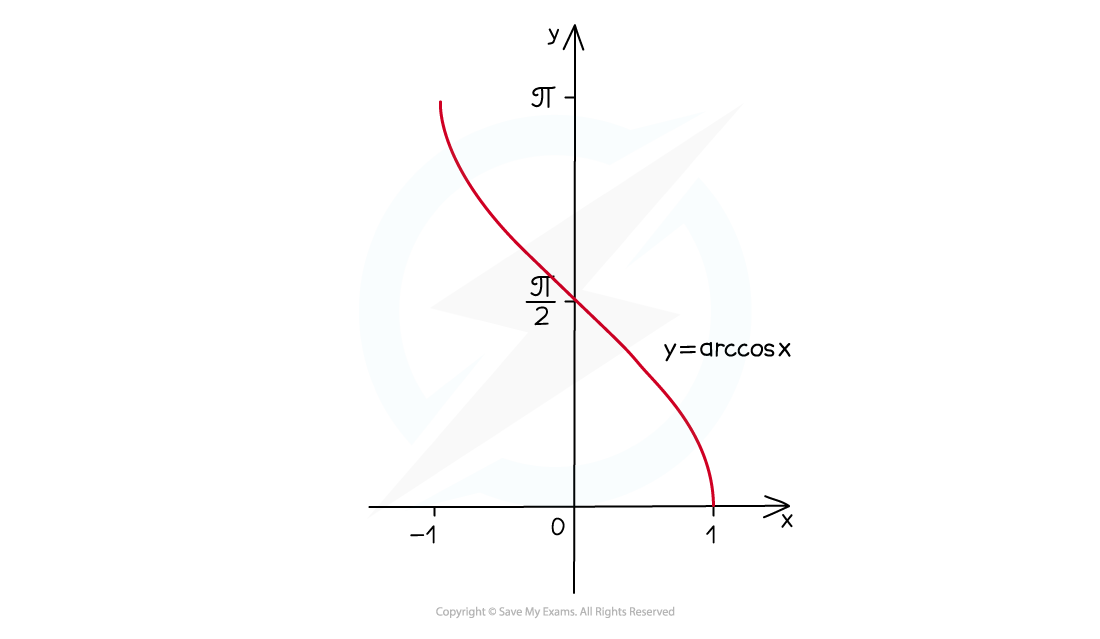
- the domain is -1 ≤ x ≤ 1
- the range is 0 ≤ arccos x ≤ π (0° ≤ arccos x ≤ 180°)
What does the graph of arctan look like?
- The graph of y = arctan x looks like this:
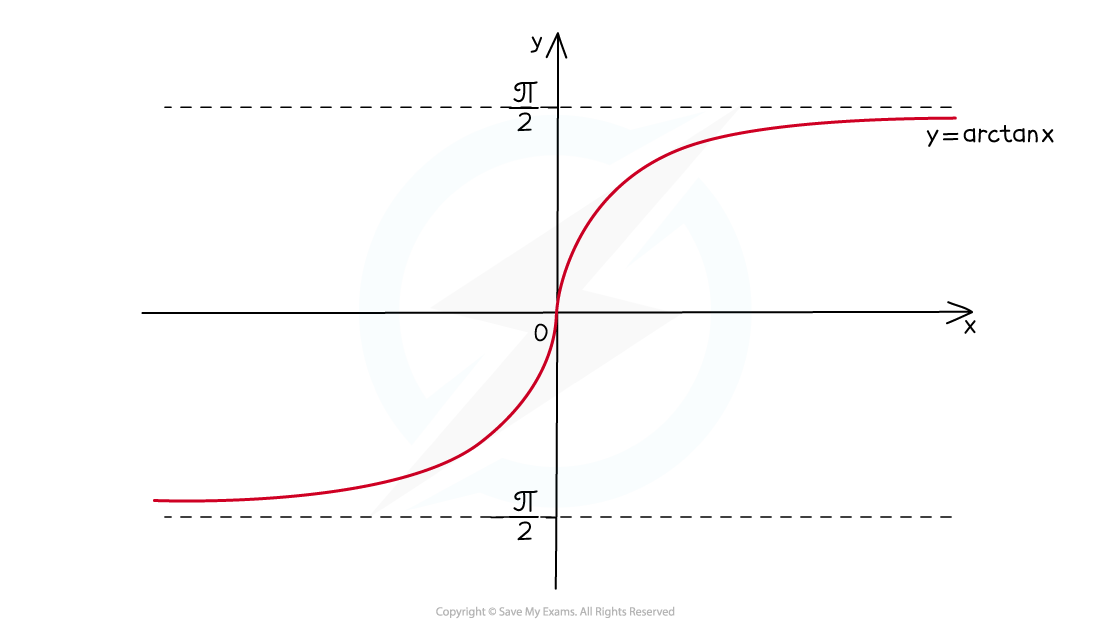
- the domain is x ∈ ℝ (ie arctan x is defined for all real number values of x)
- the range is -π/2 < arctan x < π/2 (-90° < arctan x < 90°)
- horizontal asymptotes at y= - π/2 and y = -π/2
Exam Tip
- Make sure you know the shapes of the graphs for sin, cos and tan.
- As inverses, the graphs of arcsin, arccos and arctan are reflections of sin, cos and tan in the line y = x.
- The values returned by the sin-1, cos-1 and tan-1 keys on your calculator are the values from the ranges of arcsin, arccos and arctan.
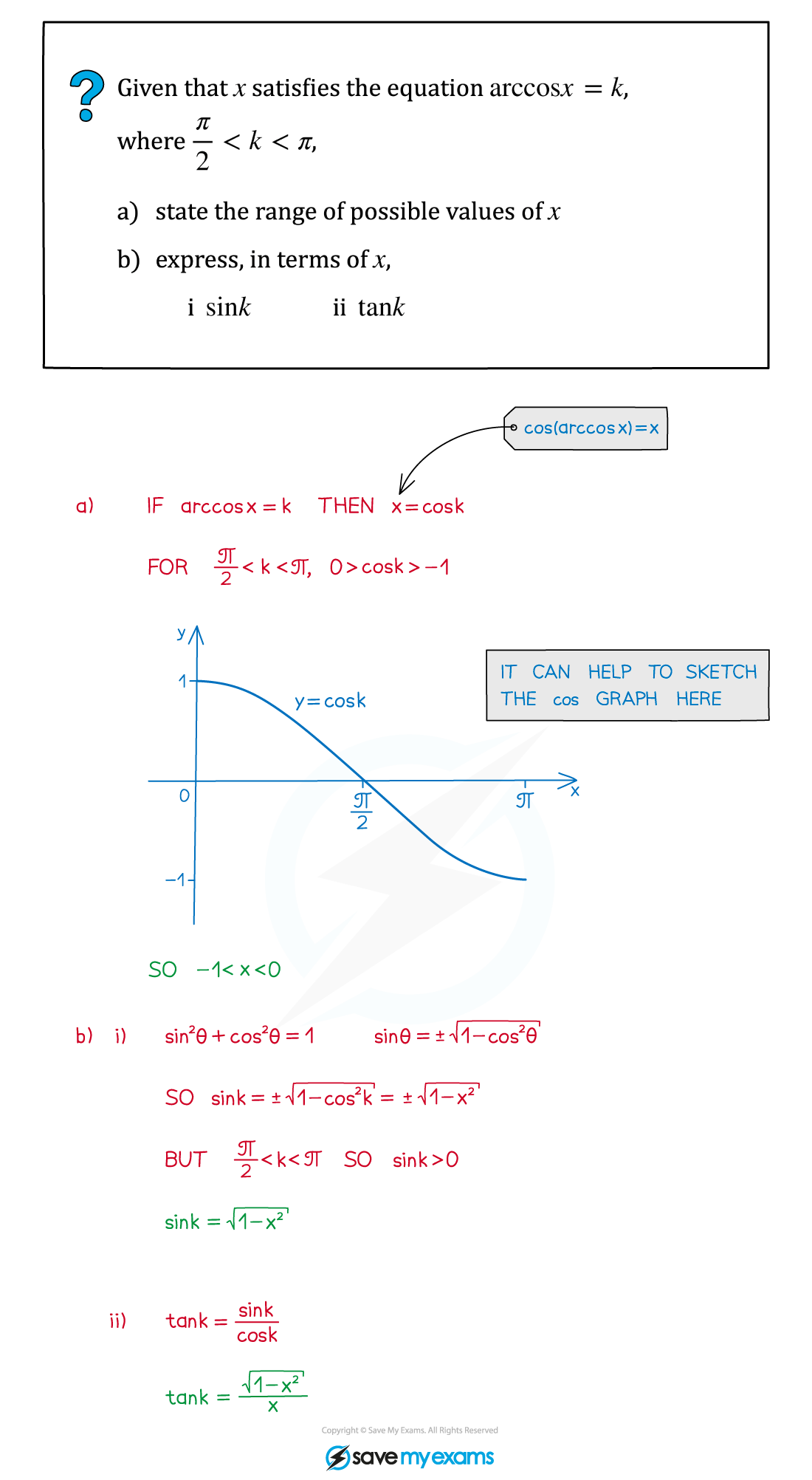
Worked Example
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





