- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
AQA A Level Maths: Pure复习笔记5.3.3 Quadratic Trigonometric Equations
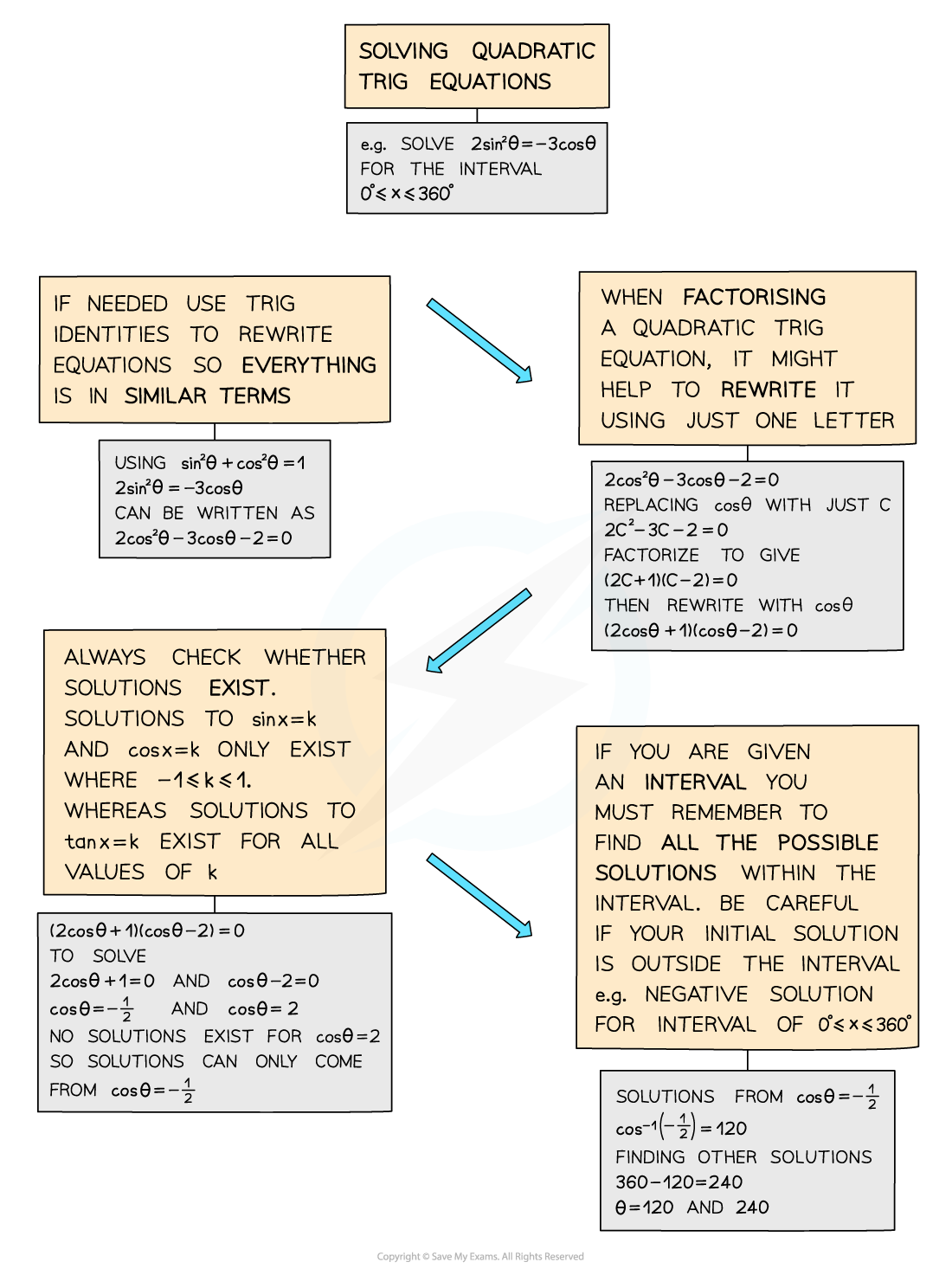
Quadratic Trigonometric Equations
Solving quadratic trigonometric equations
- If an equation involves sin2θ or cos2θ then it is a quadratic trigonometric equation
- These can be solved by factorising and/or using trigonometric identities (see Trigonometry – Simple Identities)
- As a quadratic can result in two solutions, will need to consider whether each solution exists and then find all solutions within a given interval for each
Exam Tip
- Sketch the appropriate sin, cos, tan graph to ensure you find ALL solutions within the given interval, and be super-careful if you get a negative solution but have a positive interval.
- For example, for an equation, in the interval 0° ≤ x ≤ 360°, with solution sin x = ‑¼ then sin‑1(‑¼) = -14.5 (to 1d.p.), which is not between 0 and 360 – by sketching the graph you’ll be able to spot the two solutions will be 180 + 14.5 and 360 ‑ 14.5.
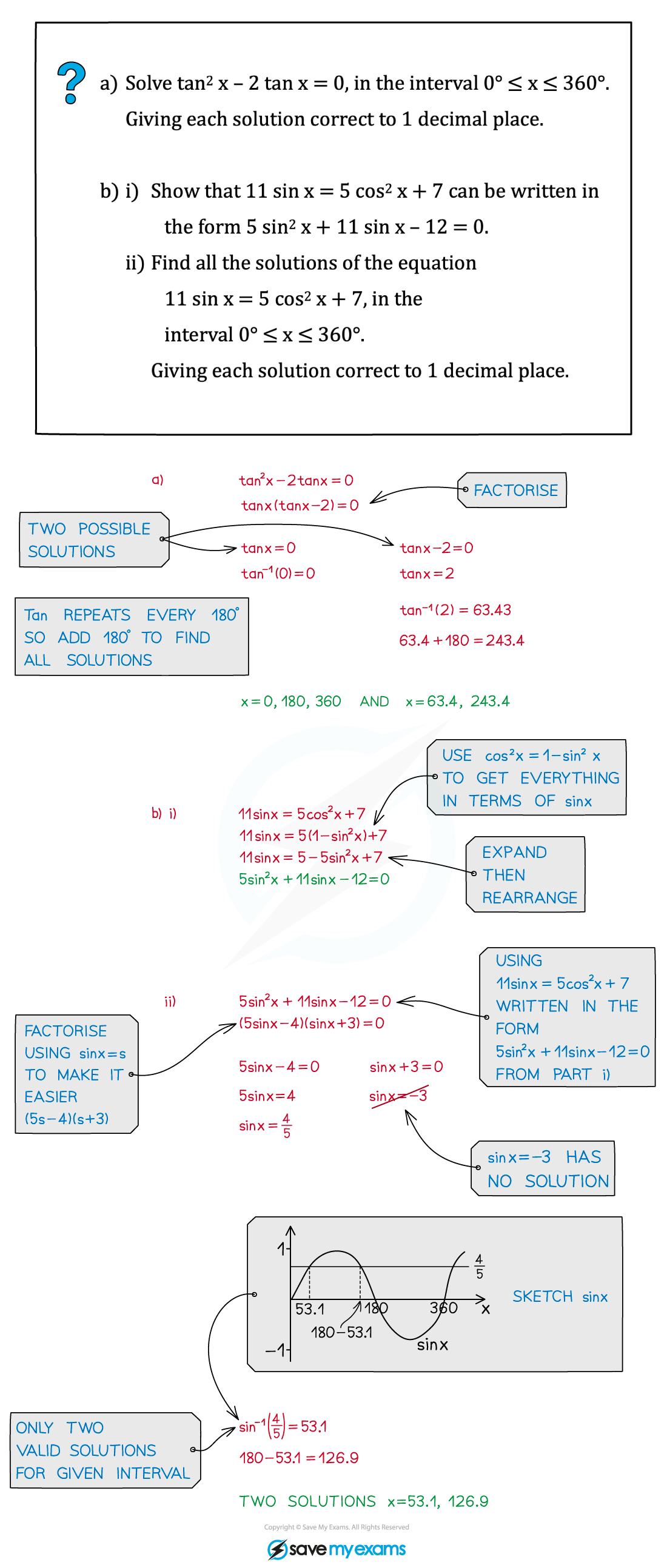
Worked Example
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





