- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: SL复习笔记7.2.3 Nuclear Fission & Fusion
Nuclear Fission & Fusion
Nuclear Fusion
- Fusion is defined as:
The joining of two small nuclei to produce a larger nucleus
- Low mass nuclei (such as hydrogen and helium) can undergo fusion and release energy
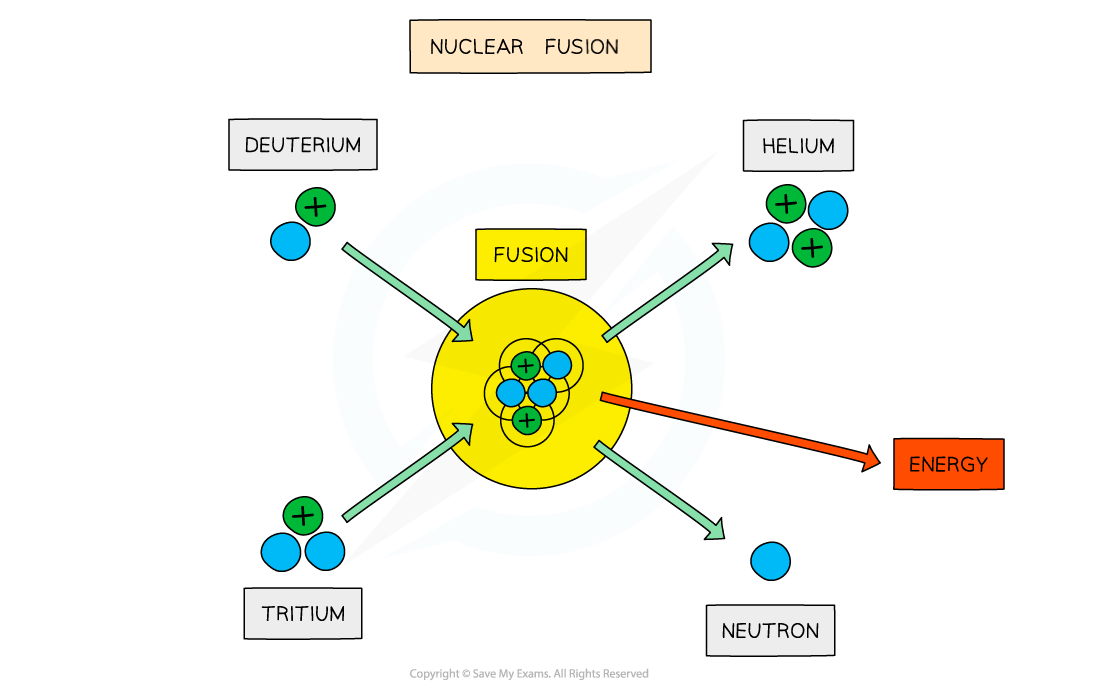
The fusion of deuterium and tritium to form helium with the release of energy
- For two nuclei to fuse, both nuclei must have high kinetic energy
- This is because the protons inside the nuclei are positively charged, which means that they repel one another
- It takes a great deal of energy to overcome the electrostatic force of repulsion.
- This can only be achieved in an extremely high-energy environment, such as star’s core
- The final step of fusion is where a nucleus of tritium fuses with a nucleus of deuterium to form a helium nucleus and a neutron. It also releases energy.
Nuclear Fission
- Fission is defined as:
The splitting of a large atomic nucleus into smaller nuclei
- High mass nuclei (such as uranium) can undergo fission and release energy
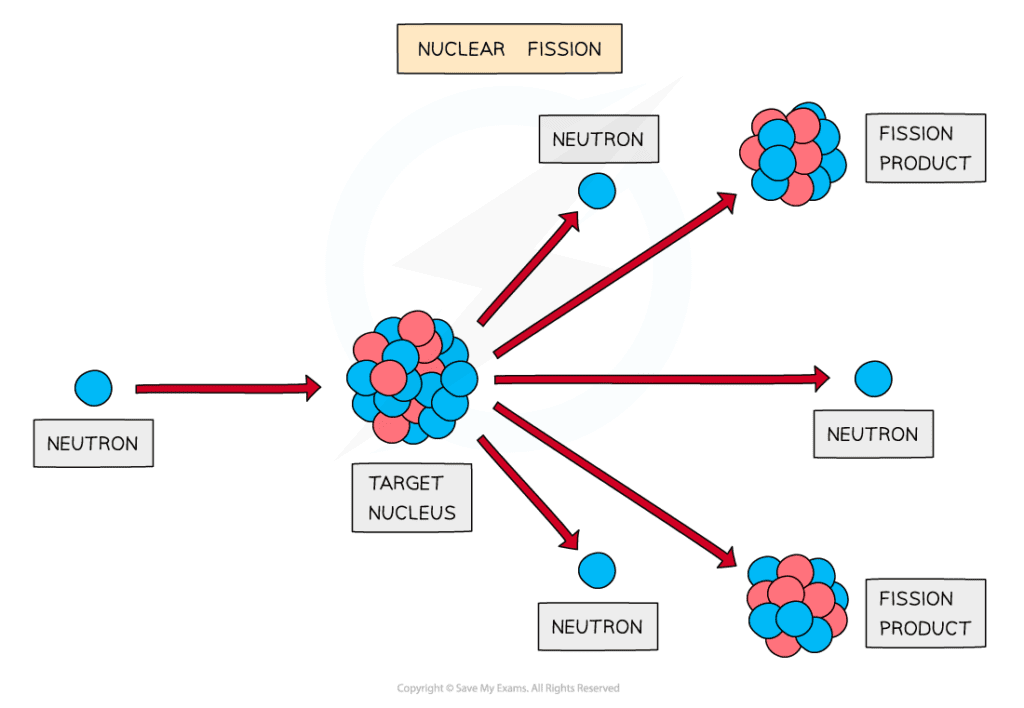
The fission of a target nucleus, such as uranium, to produce smaller daughter nuclei with the release of energy
- Fission can be induced by firing neutrons at a nucleus
- When the nucleus is struck by a neutron, it splits into two, or more, daughter nuclei
- During fission, neutrons are ejected from the nucleus, which in turn, can collide with other nuclei which triggers a cascade effect
- This leads to a chain reaction which lasts until all of the material has undergone fission, or the reaction is halted by a moderator
- Nuclear fission is the process which produces energy in nuclear power stations, where it is well controlled
- When nuclear fission is not controlled, the chain reaction can cascade to produce the effects of a nuclear bomb
Significance of Binding Energy per Nucleon
- The number of protons in the nucleus is denoted by the symbol A
- At low values of A (a small number of protons):
- Attractive strong nuclear forces between nucleons dominate over repulsive electrostatic forces between protons
- In the right conditions, nuclei undergo fusion
- During fusion, the mass of the nucleus that is created is slightly less than the total mass of the original nuclei
- The mass defect is equal to the binding energy that is released, since the nucleus that is formed is more stable
- At high values of A (a large number of protons):
- Repulsive electrostatic forces between protons begin to dominate, and these forces tend to break apart the nucleus rather than hold it together
- In the right conditions, nuclei undergo fission
- During fission, an unstable nucleus is converted into more stable nuclei with a smaller total mass
- This difference in mass, the mass defect, is equal to the binding energy that is released
Exam Tip
When an atom undergoes nuclear fission, take note that extra neutrons are ejected by the nucleus and not from the fission products.
Calculating Energy Released in Nuclear Reactions
- The binding energy is equal to the amount of energy released in forming the nucleus, and can be calculated using:
E = (Δm)c2
- Where:
- E = Binding energy released (J)
- Δm = mass defect (kg)
- c = speed of light (m s–1)
- The daughter nuclei produced as a result of both fission and fusion have a higher binding energy per nucleon than the parent nuclei
- Therefore, energy is released as a result of the mass difference between the parent nuclei and the daughter nuclei
Worked Example

Part (a)
Step 1: Balance the number of protons on each side using the proton number
92 = (2 × 46) + xnp (where np is the number of protons in c)
xnp = 92 – 92 = 0
-
-
- Therefore, c must be a neutron since the proton number is 0
-
Step 2: Balance the number of nucleons on each side using the nucleon number
235 + 1 = (2 × 116) + x
x = 235 + 1 – 232 = 4
-
-
- Therefore, 4 neutrons are generated in the reaction
-
Part (b)
Step 1: Find the binding energy of each nucleus
Total binding energy of each nucleus = Binding energy per nucleon × Mass number
Binding energy of 95Sr = 8.74 × 95 = 830.3 MeV
Binding energy of 139Xe = 8.39 × 139 = 1166.21 MeV
Binding energy of 235U = 7.60 × 235 = 1786 MeV
Step 2: Calculate the difference in energy between the products and reactants
Energy released in reaction 1 = ESr + EXe – EU
Energy released in reaction 1 = 830.3 + 1166.21 – 1786
Energy released in reaction 1 = 210.5 MeV
Part (c)
-
- Since reaction 1 releases more energy than reaction 2, its end products will have a higher binding energy per nucleon
- Hence they will be more stable
- Since reaction 1 releases more energy than reaction 2, its end products will have a higher binding energy per nucleon
-
- This is because the more energy is released, the further it moves up the graph of binding energy per nucleon against nucleon number (A)
- Since at high values of A, binding energy per nucleon gradually decreases with A
- This is because the more energy is released, the further it moves up the graph of binding energy per nucleon against nucleon number (A)
-
- Nuclear reactions will tend to favour the more stable route, therefore, reaction 1 is more likely to happen
Worked Example
When a uranium-235 nucleus absorbs a slow-moving neutron and undergoes fission one possible pair of fission fragments is technetium-112 and indium-122. The equation for this process and the binding energy per nucleon for each isotope is shown below.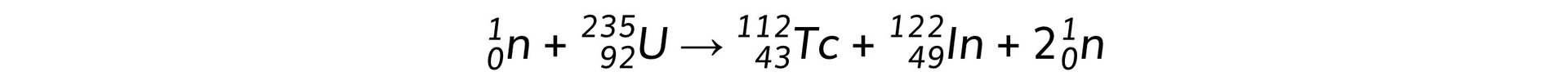
Binding energy per nucleon of U-235 = 7.59 MeV
Binding energy per nucleon of Tc-112 = 8.36 MeV
Binding energy per nucleon of In-122 = 8.51 MeV
When a uranium-235 nucleus undergoes fission in this way, calculate:
a) The energy released, in MeV
b) The mass defect
Part (a)
Step 1: Determine the binding energies on each side of the equation
Binding energy = Binding Energy per Nucleon × Mass Number
-
-
- Binding energy before (U) = 235 × 7.59 = 1784 MeV
- Binding energy after (Tc + In) = (112 × 8.36) + (122 × 8.51) = 1975 MeV
-
Step 2: Find the difference between the energies
-
-
- Energy released = 1975 – 1784 = 191 MeV
-
Part (b)
Method 1
Step 1: Convert the energy released from MeV to J
-
-
- 1 MeV = 1.60 × 10−13 J
- Energy released = 191 × (1.60 × 10−13) = 3.06 × 10−11 J
-
Step 2: Write down the equation for mass-energy equivalence
E = Δmc2
-
-
- Where c = speed of light
-
Step 3: Rearrange and determine the mass defect, Δm
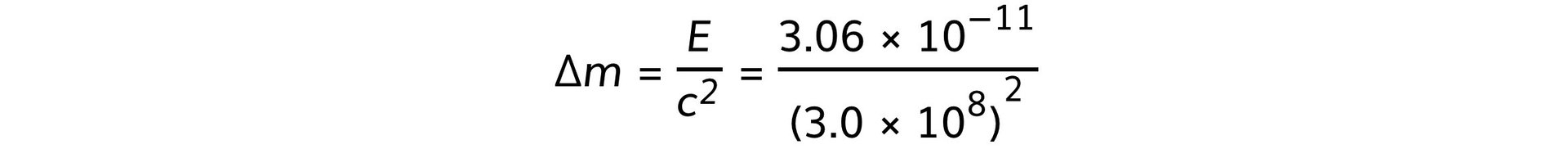
Δm = 3.4 × 10−28 kg
Method 2
Step 1: Convert the energy released from MeV to u
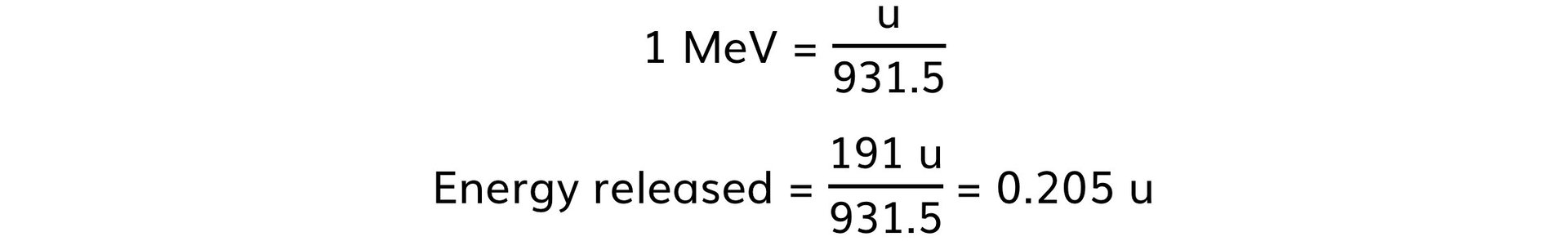
Step 2: Calculate the mass defect, Δm
-
-
- 1 u = 1.66 × 10−27 kg
-
Δm = 0.205 × (1.66 × 10−27) = 3.4 × 10−28 kg
Exam Tip
Both methods for calculating mass defect in the second worked example are perfectly valid. It is highly recommended that you practice both ways and see which method you are most comfortable using.
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





