- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: SL复习笔记5.2.2 Resistance & Resistors
Resistance
- As electrons move through the metal wire of a circuit (or any other component), they transfer some of their electrical potential energy to the positive ions of the metal
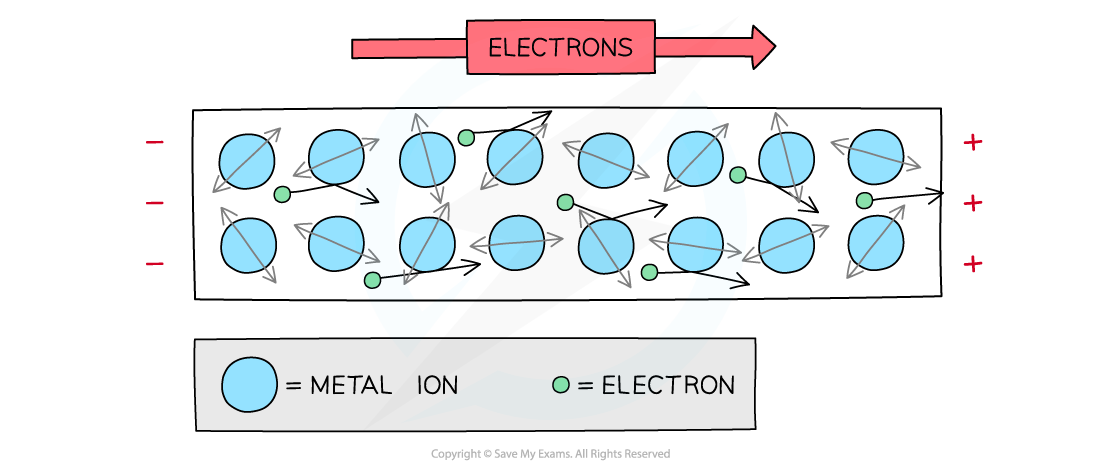
Free electrons collide with metal ions which resist their flow
- This energy results in an increase in the kinetic energy of the lattice
- Which means a higher internal energy of the metal
- The macroscopic result of this transfer is the heating up of the wire
- Some metals heat up more than others
- The higher the heating, the higher the resistance
- Wires are often made from copper because copper has a low electrical resistance
- The resistance R of a component is defined as:
The ratio of the potential difference across the component to the current flowing through it
- It is calculated as follows:
![]()
- Where:
- V = potential difference in volts (V)
- I = electric current in amperes (A)
- R = resistance in ohms (Ω)
- This means that the higher the resistance of a component, the lower the current flowing through it and vice versa
- In terms of SI base units: 1 Ω = 1 kg m2 s–3 A–2
Worked Example
A charge of 5.0 C passes through a resistor at a constant rate in 30 s. The potential difference across the resistor is 2.0 V.
Calculate the resistance R of the resistor.
Step 1: Write down the known quantities
-
- Charge, Δq = 5.0 C
- Time, Δt = 30 s
- Potential difference, V = 2.0 V
Step 2: Write down the equation for the resistance R
![]()
Step 3: Calculate the current I from the charge and time
![]()
Step 4: Substitute the numbers into the above equation
![]()
I = 0.17 A
Step 5: Substitute this value of the current into the equation for the resistance given in Step 2
![]()
R = 12 Ω
Resistors in Series & Parallel
Resistors in Series
- When two or more components are connected in series:

The combined resistance of the components is equal to the sum of individual resistances

- This means as more resistors are added, their combined resistance increases and is, therefore, more than the resistance of the individual components
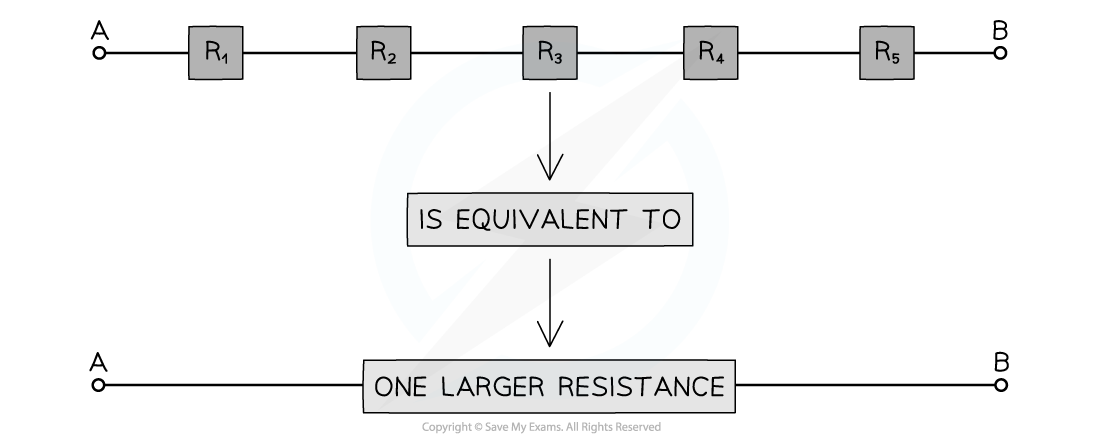
Connecting more resistors in series increases the overall resistance
Worked Example
The combined resistance R in the following series circuit is 60 Ω. What is the resistance value of R2?
A. 100 Ω B. 30 Ω C. 20 Ω D. 40 Ω
Step 1: Write down the known quantities
-
- Total resistance, R = 60 Ω
- Resistance of first resistor, R1 = 30 Ω
- Resistance of third resistor, R3 = 10 Ω
Step 2: Write down the equation for the combined resistance of resistors in series
R = R1 + R2 + R3
Step 3: Rearrange the above equation to calculate the resistance R2 of the second resistor
R2 = R – R1 – R3
Step 4: Substitute the numbers into the above equation
R2 = (60 – 30 – 10) Ω
R2 = 20 Ω
ANSWER: C
Resistors in Parallel
- When two or more components are connected in parallel:

The reciprocal of the combined resistance is the sum of the reciprocals of the individual resistances

- This means as more resistors are added, their combined resistance decreases and is, therefore, less than the resistance of the individual components
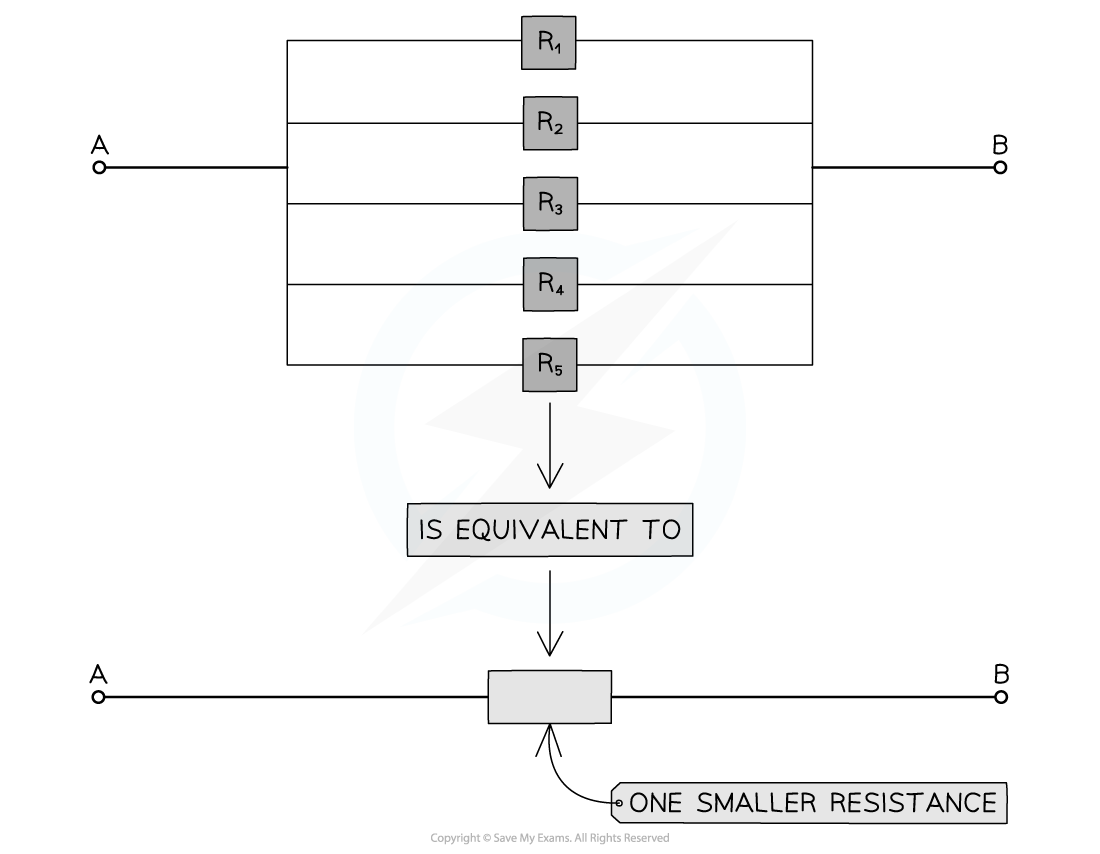
Connecting more resistors in parallel decreases the overall resistance
Worked Example
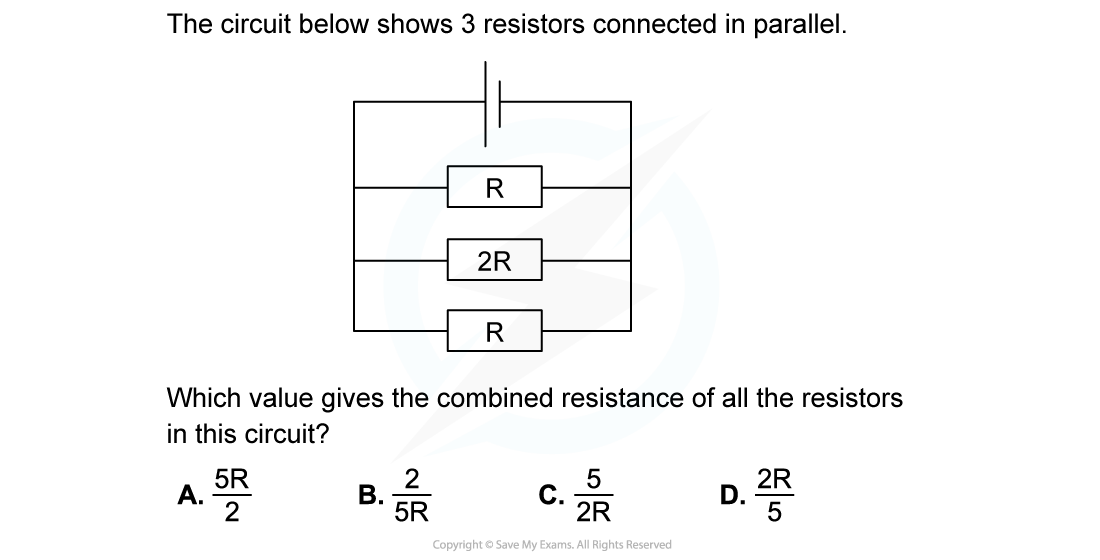
Step 1: Write down the known quantities
-
- Resistance of first resistor, R1 = R
- Resistance of second resistor, R2 = 2R
- Resistance of third resistor, R3 = R
Step 2: Write down the equation for the reciprocal of the combined resistance (1/RTOT) of resistors in parallel
![]()
Step 3: Substitute the given quantities into the above equation
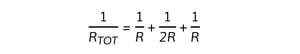
![]()
Step 4: Take the reciprocal of the second equation above to get the combined resistance RTOT
![]()
ANSWER: D
Exam Tip
The most common mistake in questions about parallel resistors is to forget to find the reciprocal of RT (i.e. 1/RT) instead of RT. Here is a maths tip to rejig your memory on reciprocals:
- The reciprocal of a value is 1 / value
- For example, the reciprocal of a whole number such as 2 equals ½
- Conversely, the reciprocal of ½ is 2
- If the number is already a fraction, the numerator and denominator are ‘flipped’ round
 The reciprocal of a number is 1 ÷ number
The reciprocal of a number is 1 ÷ number
- In the case of the resistance R, this becomes 1/R
- To get the value of R from 1/R, you must calculate 1 ÷ your answer
- You can also use the reciprocal button on your calculator (labelled either x –1 or 1/x, depending on your calculator)
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





