- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: SL复习笔记4.5.4 Harmonics
Harmonics
- Stationary waves can have different wave patterns, known as harmonics
- These depend on the frequency of the vibration and the boundary conditions (i.e. fixed and/or free ends)
- The harmonics are the only frequencies and wavelengths that will form standing waves on strings or in pipes
Harmonics on Strings
- The boundary condition is that both ends are fixed
- The simplest wave pattern is a single loop made up of two nodes (i.e. the two fixed ends) and an antinode
- This is called the first harmonic
- The wavelength of this harmonic is λ1 = 2L
- Using the wave equation, the frequency is f1 = v/2L, where v is the wave speed of the travelling waves on the string (i.e. the incident wave and the reflected wave)
- As the vibrating frequency increases, more complex patterns arise
- The second harmonic has three nodes and two antinodes
- The third harmonic has four nodes and three antinodes
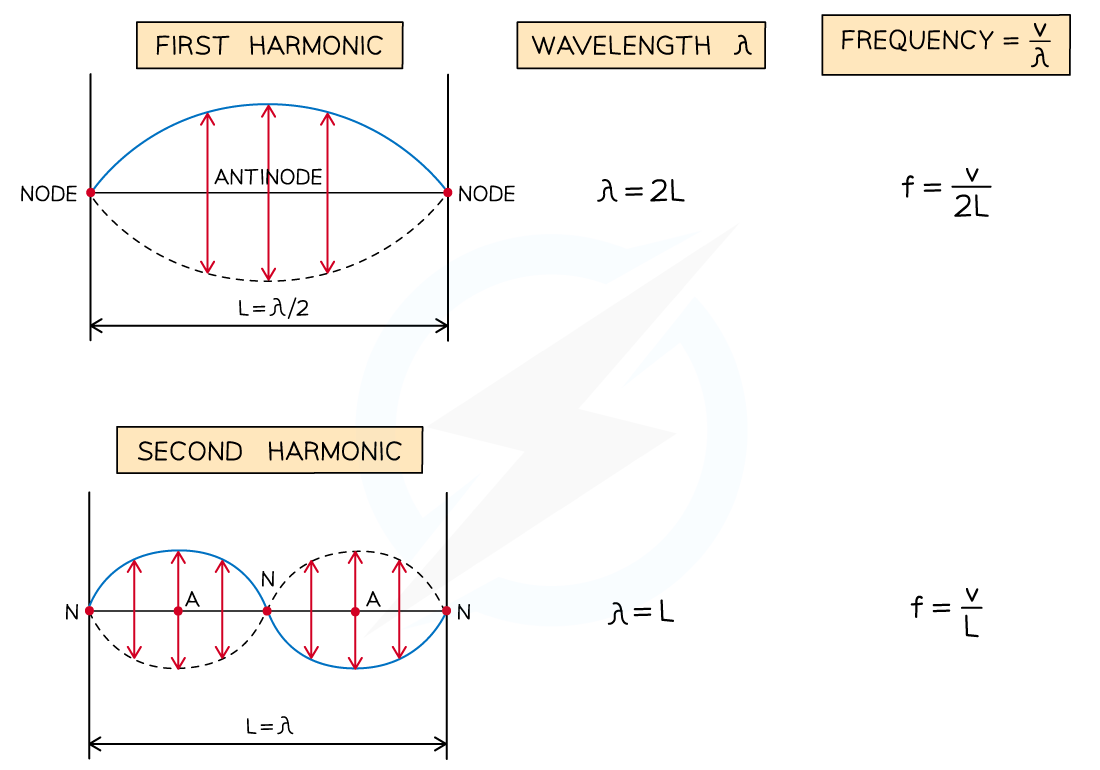

Diagram showing the first three harmonics on a stretched string fixed at both ends
- The nth harmonic will have (n + 1) nodes and n antinodes
- The general expression for the wavelength of the nth harmonic on a string that is fixed at both ends is:
![]()
- Where:
- λn = wavelength in metres (m)
- L = length of the string in metres (m)
- n = integer number greater than zero - i.e. 1, 2, 3...
- Knowing the wavelength λn of the standing wave and the speed v of the travelling waves (i.e. incident and reflected), the natural frequency fn of any harmonic can be calculated using the wave equation v = fλn, so that:
![]()
Harmonics in Pipes
- The boundary conditions vary, since pipes can have:
- two open ends
- only one open end
- For a pipe that is open at both ends:
- The simplest wave pattern is one central node and two antinodes
- The second harmonic consists of two nodes and three antinodes
- The nth harmonic will have (n + 1) antinodes and n nodes
- The expression for the wavelength of the nth harmonic in a pipe of length L is the same as that given above for nth harmonic on a string
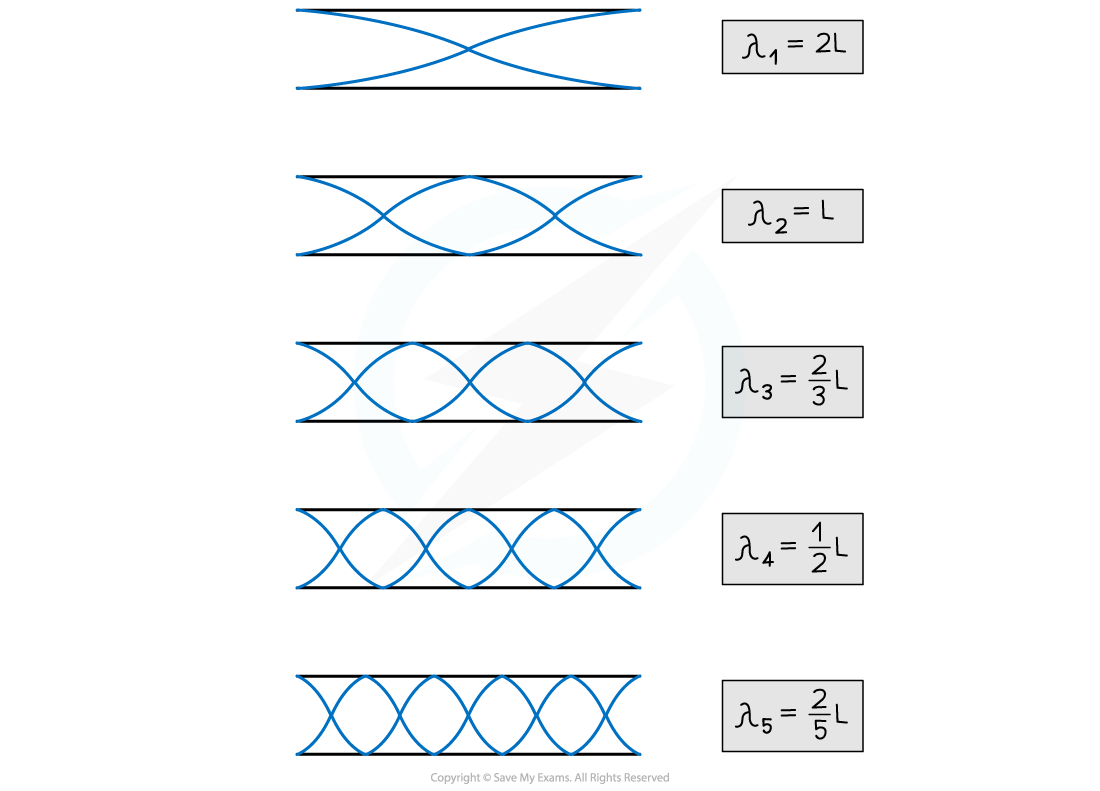
Diagram showing the first five harmonics in a pipe open at both ends
- For a pipe that is open at one end:
- The lowest harmonic is a "half-loop" with one node and one antinode
- The next possible harmonic will have two nodes and two antinodes
- This is the third harmonic, not the second one
- Since only odd harmonics can exist under this boundary condition

Diagram showing the first three possible harmonics in a pipe open at one end. Only the odd harmonics can form in this case
-
- The expression for the wavelength of the nth harmonic in a pipe of length L is:
![]()
-
- Where this time, n is an odd number - i.e. 1, 3, 5...
- Under both boundary conditions, the natural frequencies are once again calculated from the wavelength of the standing wave and the speed v of the travelling waves using the wave equation
Worked Example
Transverse waves travel along a stretched wire 100 cm long. The speed of the waves is 250 m s–1.
Determine the maximum harmonic detectable by a person who can hear up to 15 kHz.
Step 1: Write down the known quantities
-
- L = 100 cm = 1.00 m
- v = 250 m s–1
- fn = 15 kHz = 15000 Hz
Note the conversions:
-
- The length must be converted from centimetres (cm) into metres (m)
- The frequency must be converted from kilohertz (kHz) into hertz (Hz)
Step 2: Write down the equation for the frequency of the nth harmonic
![]()
Step 3: Rearrange the above equation to calculate the number n of the maximum harmonic detectable by the person
![]()
Step 4: Substitute the numbers into the above equation
![]()
n = 120
The person can hear up to the 120th harmonic
Exam Tip
Before carrying out any calculation on standing waves, you should look carefully at the boundary conditions, since these will determine the wavelengths and natural frequencies of the harmonics.
The expressions for the wavelength of the nth harmonic on strings fixed at both ends (or in pipes open at both ends) and in pipes open at one end are not given in the data booklet and you must be able to recall them.
Remember that n can take any integer value greater than zero in the case of standing waves on strings and in pipes open at both ends. For pipes open at one end, instead, n can only be an odd integer.
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





