- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: SL复习笔记4.5.3 Boundary Conditions for Standing Waves
Boundary Conditions
- Stationary waves can form on strings or in pipes
- In both cases, progressive waves travel in a medium (i.e. the string or air) and superimpose with their reflections
- The number of nodes and antinodes that fit within the available length of medium depends on:
- The frequency of the progressive waves
- The boundary conditions (i.e. whether the progressive waves travel between two fixed ends, two free ends or a fixed and a free end)
Standing Waves on Stretched Strings
- When guitar strings are plucked, they can vibrate with different frequencies
- The frequency with which a string vibrates depends on:
- The tension, which is adjusted using rotating 'tuning pegs'
- The mass per unit length, which is the reason why a guitar has strings of different thicknesses
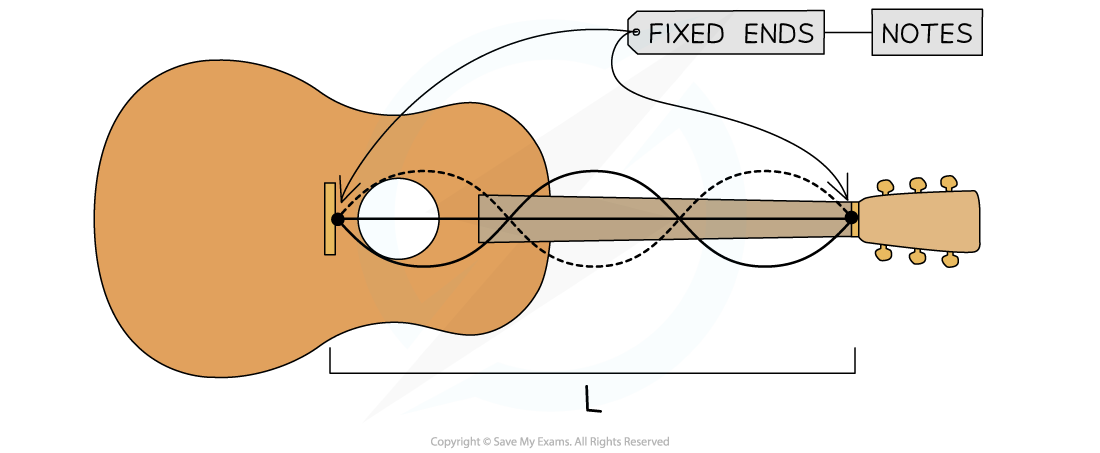
Standing wave on a guitar string
- For a string, the boundary condition can be
- Fixed at both ends
- Free at both ends
- One end fixed, the other free
- At specific frequencies, known as natural frequencies, an integer number of half wavelengths will fit on the length of the string
- As progressive waves of different natural frequencies are sent along the string, standing waves with different numbers of nodes and antinodes form
Standing Waves in Pipes
- When the air within a pipe vibrates, longitudinal waves travel along the pipe
- Simply blowing across the open end of a pipe can produce a standing wave in the pipe
- For a pipe, there is more than one possible boundary condition, theses are pipes that are:
- Closed at both ends
- Open at both ends
- Closed at one end and open on the other
Nodes & Antinodes
- When a progressive wave travels towards a free end for a string, or open end for a pipe:
- The reflected wave is in phase with the incident wave
- The amplitudes of the incident and reflected waves add up
- A free end is a location of maximum displacement - i.e. an antinode

Standing wave inside a pipe open at both ends
- When a progressive wave travels towards a fixed end for a string, or closed end for a pipe:
- The reflected wave is in anti-phase with the incident wave
- The two waves cancel out
- A fixed end is a location of zero displacement - i.e. a node
- The open end is therefore a location of maximum displacement - i.e. an antinode

Standing wave inside a pipe open at both ends
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





