- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: SL复习笔记4.4.5 Single-Slit Diffraction
Single-Slit Diffraction
- Diffraction is the spreading out of waves when they pass an obstruction
- This obstruction is typically a narrow slit known as an aperture
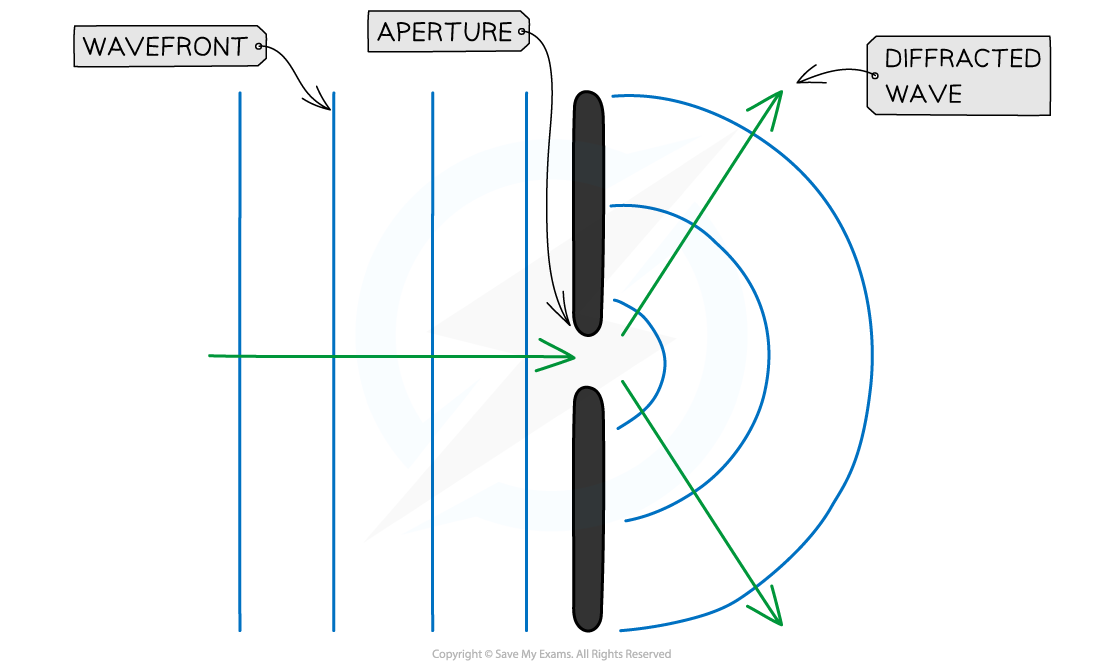
As waves pass through the aperture, they spread out
- The frequency of the diffracted waves is less than that of the incident waves, since energy is distributed over a larger area
- The extent of diffraction depends on the width of the gap compared to the wavelength of the wave
- Diffraction is the most prominent when the width of the slit is approximately equal to or smaller than the wavelength
- As the gap size increases, the effect gradually gets less pronounced until, in the case that the gap is much larger than the wavelength, the waves are no longer spread out
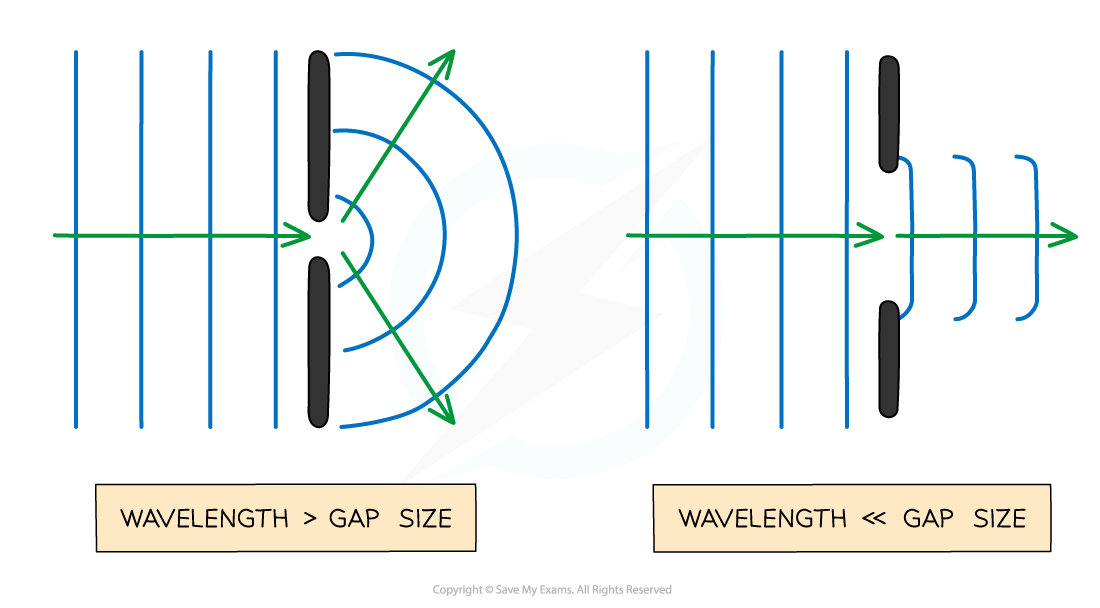
The size of the gap (compared to the wavelength) affects how much the waves spread out
- Any type of wave can be diffracted i.e. sound, light, water
- The only property of a wave that changes when its diffracted is its amplitude
- This is because some energy is dissipated when a wave is diffracted through a gap
- Diffraction can also occur when waves curve around an edge:
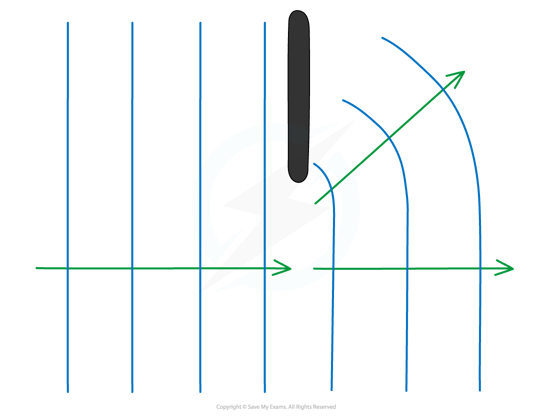
When a wave goes past the edge of a barrier, the waves can curve around it
Worked Example
An electric guitar student is practising in his room. He has not completely shut the door of his room, and there is a gap of about 10 cm between the door and the door frame.
Determine the frequencies of sound that are best diffracted through the gap.
The speed of sound can be taken to be 340 m s–1
Step 1: Optimal diffraction happens when the wavelength of the waves is comparable to (or larger than) the size of the gap
λ = 10 cm = 0.1 m
Step 2: Write down the wave equation
c = fλ
-
- where c = 340 m s–1
Step 3: Rearrange the above equation for the frequency f
![]()
Step 4: Substitute the numbers into the above equation
![]()
f = 3400 Hz
The frequencies of sound that are best diffracted through the gap are:
f ≤ 3400 Hz
Worked Example
When a wave is travelling through the air, which scenario best demonstrates diffraction?
A. UV radiation through a gate post
B. Sound waves passing a diffraction grating
C. Radio waves passing between human hair
D. X-rays passing through atoms in a crystalline solid
ANSWER: D
- Diffraction is most prominent when the wavelength is close to the aperture size
Consider option A:
- UV waves have a wavelength between (4 × 10–7) and (1 × 10–8) m so would not be diffracted by a gate post
- Radio waves, microwaves or sound waves would be more likely to be diffracted at this scale
Consider option B:
- Sound waves have a wavelength of (1.72 × 10–2) to 17 m so would not be diffracted by the diffraction grating
- Infrared, light and ultraviolet waves would be more likely to be diffracted at this scale
Consider option C:
- Radio waves have a wavelength of 0.1 to 106 m so would not be diffracted by human hair
- Infrared, light and ultraviolet waves would be more likely to be diffracted at this scale
Consider option D:
- X-rays have a wavelength of (1 × 10–8) to (4 × 10–13) m
- This is a suitable estimate for the size of the gap between atoms in a crystalline solid
- Hence X-rays could be diffracted by a crystalline solid
- Therefore, the correct answer is D
Exam Tip
When drawing diffracted waves, take care to keep the wavelength (the distance between each wavefront) constant.
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





