- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: SL复习笔记4.1.4 Energy in SHM
Energy in SHM
- The total energy of an object oscillating with SHM is the sum of its potential energy (gravitational or elastic) and kinetic energy
E = EP + EK
- Where:
- E = total energy in joules (J)
- EP = potential energy in joules (J)
- EK = kinetic energy in joules (J)
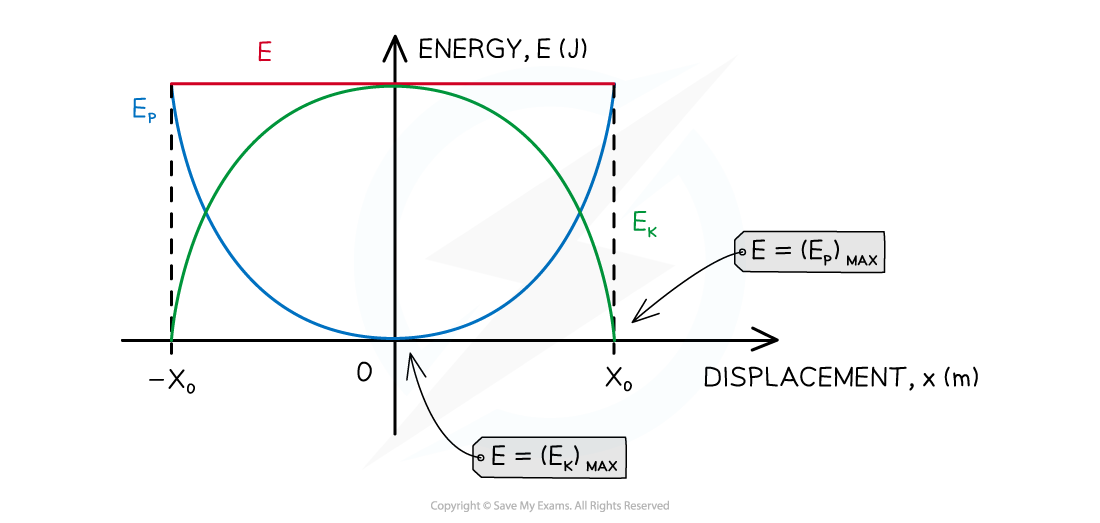
Graph of total energy E, potential energy EP and kinetic energy EK of an object oscillating with SHM
- If energy losses due to friction or drag are zero or ignored, the total energy E of the system is conserved
- The potential energy store of the object is at a maximum at the point of maximum displacement from the equilibrium position
- The point of maximum displacement is amplitude x0
- Kinetic energy is zero at amplitude
- Potential energy is equal to the total energy of the system at this point
- Energy is transferred from the object's potential energy store to its kinetic energy store as the object moves from amplitude to the equilibrium position
- The object has both potential and kinetic energy
- The sum of the potential and kinetic energy is equal to the total energy of the system
- The total energy of the system is conserved
- The kinetic energy store of the object is at a maximum at the equilibrium position
- This is because velocity is at a maximum as the object passes through the equilibrium position
- Kinetic energy is equal to the total energy of the system at this point
- Energy is transferred from the object's kinetic energy store to its potential energy store as the object moves from the equilibrium position to amplitude
- The object has both potential and kinetic energy
- The sum of the potential and kinetic energy is equal to the total energy of the system
- The total energy of the system is conserved
Worked Example
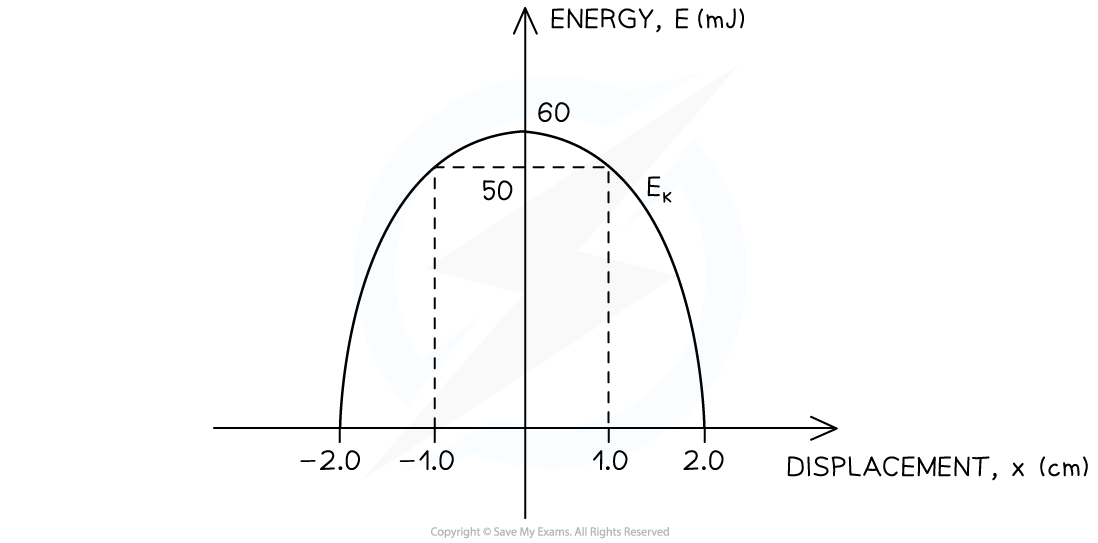
(i) Determine the total energy of the object
(ii) Determine the amplitude of the object's oscillations
(iii) Calculate the maximum velocity of the object in metres per second (m s–1)
(iv) Determine the potential energy of the object when the displacement is x = 1.0 cm
(i) Determine the total energy of the object by reading the maximum value of the kinetic energy from the graph
-
- From the graph, read the maximum value of the object's kinetic energy (EK)MAX = 60 mJ
- Recall that, at the equilibrium position (x = 0), the total energy E is exactly equal to the maximum value of the kinetic energy (EK)MAX
- Since energy losses can be neglected, the total energy is constant
E = 60 mJ
(ii) Read the amplitude of the object's oscillations from the graph
-
- The maximum displacement positions are the locations on either side of the equilibrium position where the kinetic energy is zero EK = 0
x0 = 2.0 cm
(iii)
Step 1: Recall the equation for the kinetic energy EK of an object in terms of its mass m and velocity v
![]()
Step 2: Rearrange the above equation to calculate the velocity v
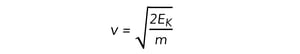
Step 3: Substitute the numbers into the equation to calculate the maximum velocity of the object
-
- Mass of the object, m = 0.50 kg
- You must convert the maximum kinetic energy must from millijoules (mJ) into joules (J)
EK = 60 mJ = 0.06 J
![]()
v = 0.49 m s–1
(iv)
Step 1: Read the value of the kinetic energy EK of the object when the displacement is x = 1.0 cm
EK = 50 mJ
Step 2: Write down the relationship between total energy E, kinetic energy EK and potential energy EP
E = EP + EK
Step 3: Rearrange the above equation to calculate the potential energy EP
EP = E – EK
Step 4: Substitute the numbers in the above equation
-
- EK = 50 mJ
- E = 60 mJ
EP = 60 mJ – 50 mJ
EP = 10 mJ
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





