- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: SL复习笔记2.2.6 Friction
Friction
- Friction is a force that works in opposition to the motion of an object
- It occurs between two solid bodies that are in contact with one another
- The opposition of friction slows down the motion of the object
- When friction is present, energy is transferred in the form of heat
- This raises the temperature (thermal energy) of the object and its surroundings
- The work done against the frictional forces causes this rise in the temperature
- Imperfections at the interface between the object and the surface bump into and rub up against each other
- Not only does this slow the object down but also causes an increase in thermal energy
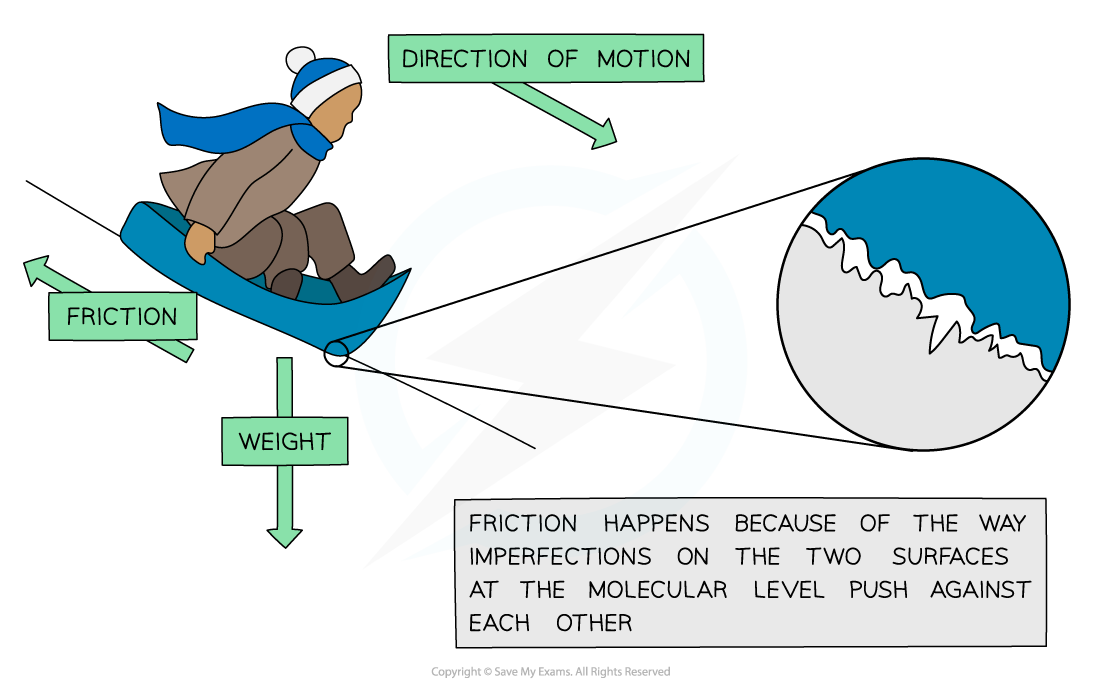
The interface between the ground and the sled is bumpy which is the source of the frictional force
Static & Dynamic Friction
- There are two kinds of friction to consider for IB DP Physics
- Static friction occurs when two solid objects are in contact and no movement is occurring between the two objects
- Dynamic friction occurs once one of the objects is moving past the other, such as in the sled example above
- Both of these forms of friction depend on the normal reaction force of the object sitting upon the other
- Static friction will match any pushing force that acts against until it can no longer hold the two objects stationary
- Static friction increases in magnitude until movement begins and dynamic friction occurs
- For any given situation, static friction should reach a maximum value that is larger than that of dynamic friction
- For a constant pushing force, dynamic friction will be a constant
- This is because there are more forces at work keeping an object stationary than there are forces working to resist an object once it is in motion
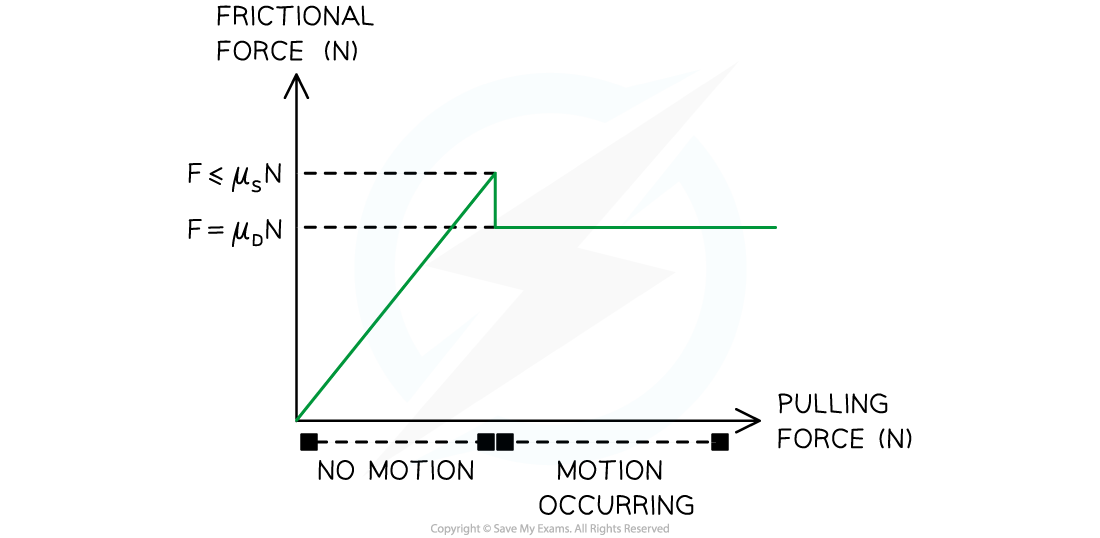
The relationship between frictional forces and motion
- The equation for static friction is given by:
F ≤ μS × R
- Where:
- F = static frictional force (N)
- μS = coefficient of static friction
- R = normal reaction force (N)
- The coefficient of static friction is a number between 0 and 1 but does not include those numbers
- It is a ratio of the force of static friction and the normal force
- The larger the coefficient of static friction, the harder it is to move those two objects past one another
- The equation for dynamic friction is given by:
F = μD × R
- Where:
- F = dynamic frictional force (N)
- μD = coefficient of dynamic friction
- R = normal reaction force (N)
- The coefficient of dynamic friction has similar properties to that of static friction
- Yet, dynamic friction has a definite force value for a given situation
- Whereas the force of static friction has an increasing force value
Worked Example
An 8.0 kg block sits on an incline of 20 degrees from the horizontal. It is stationary and does have a frictional force acting upon it.
Determine the minimum possible value of the coefficient of static friction.
Step 1: List the known quantities
-
- Mass of the block, m = 8.0 kg
- Angle between the slope and the horizontal, θ = 20°
Step 2: Determine the weight of the block
-
- The weight will act directly downwards and comes from the interaction of mass and acceleration due to gravity
W = m × g
8.0 × 9.8 = 78.4 N downwards
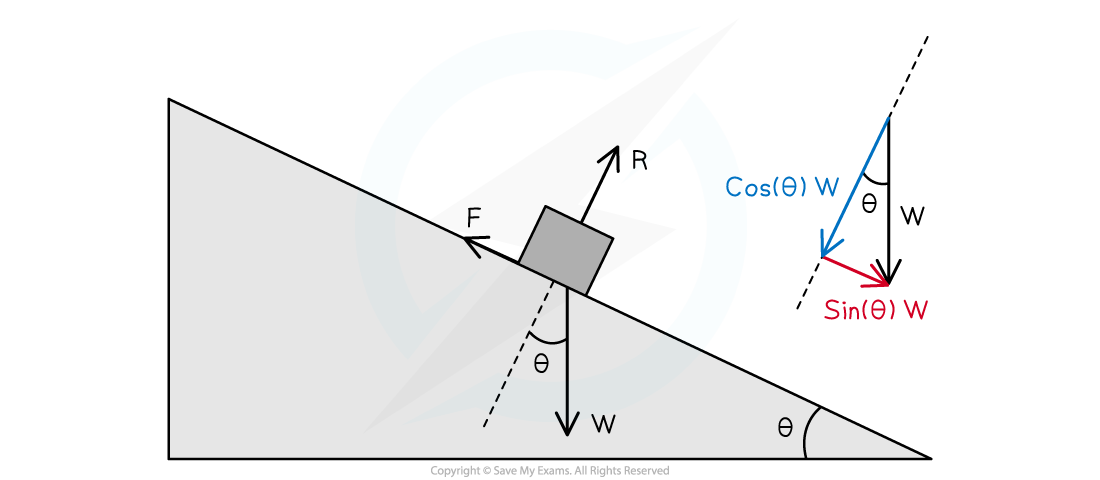
Step 3: Break the weight down into components based on the slope angle
-
- The component that is parallel to the slope and provides a force moving the block down the slope can be found from:
sin(20°) × W = F
F = sin(20°) × 78.4 = 26.8 N
-
- The component that is perpendicular to the slope and the same magnitude as the normal reaction force can be found from:
cos(20°) × W = F
F = cos(20°) × 78.4 = 73.7 N
Step 4: Use the equation of static friction to find the minimum value of the coefficient of static friction
-
- The equation for static friction is:
F ≤ μS × R
-
- In this case, the F is the 26.8 N pushing the block down the slope
- The R is the normal reaction force which has the same magnitude as the perpendicular component of the weight force which is 73.7 N
- Therefore the value can be added and μS solved for:
26.8 ≤ μS × 73.7
-
- Rearrange for μS
26.8 ÷ 73.7 ≤ μS
0.36 ≤ μS
Step 5: State the final answer
-
- The coefficient for static friction must be at least 0.36 or greater for this situation
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





