- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: SL复习笔记2.1.4 Graphs Describing Motion
Motion Graphs
- Three types of graphs that can represent motion are displacement-time graphs, velocity-time graphs, and acceleration-time graphs
Displacement-Time Graph
- On a displacement-time graph…
- Slope equals velocity
- The y-intercept equals the initial displacement
- A straight(diagonal) line represents a constant velocity
- A curved line represents an acceleration
- A positive slope represents motion in the positive direction
- A negative slope represents motion in the negative direction
- A zero slope (horizontal line) represents a state of rest
- The area under the curve is meaningless
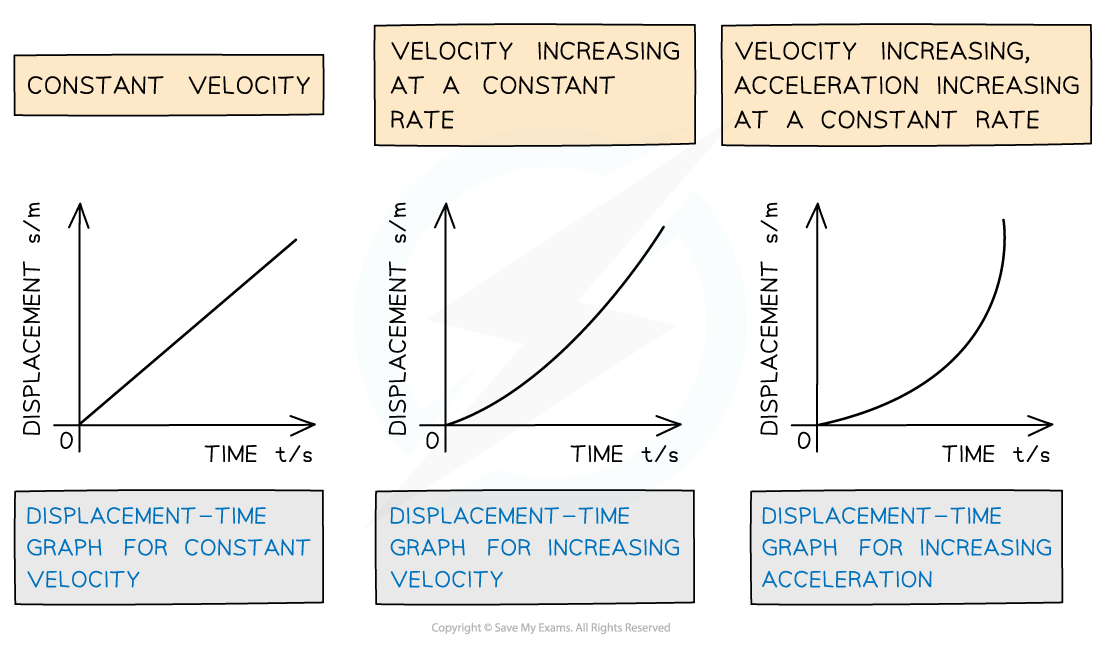 Displacement-time graphs displacing difference velocities
Displacement-time graphs displacing difference velocities
Velocity-Time Graph
- On a velocity-time graph…
- Slope equals acceleration
- The y-intercept equals the initial velocity
- A straight line represents uniform acceleration
- A curved line represents non-uniform acceleration
- A positive slope represents an increase in velocity in the positive direction
- A negative slope represents an increase in velocity in the negative direction
- A zero slope (horizontal line) represents motion with constant velocity
- The area under the curve equals the change in displacement
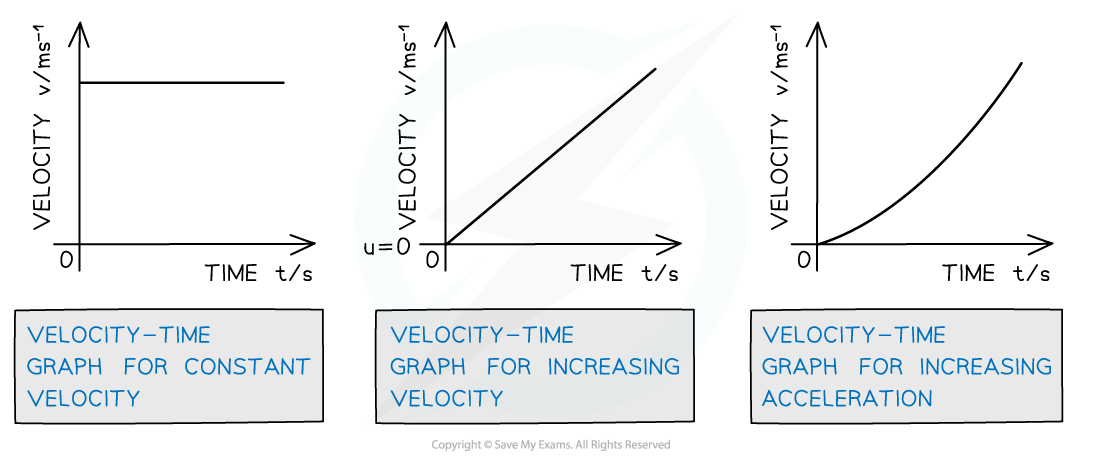 Velocity-time graphs displacing different acceleration
Velocity-time graphs displacing different acceleration
Acceleration-Time Graph
- On an acceleration-time graph…
- Slope is meaningless
- The y-intercept equals the initial acceleration
- A zero slope (horizontal line) represents an object undergoing constant acceleration
- The area under the curve equals the change in velocity
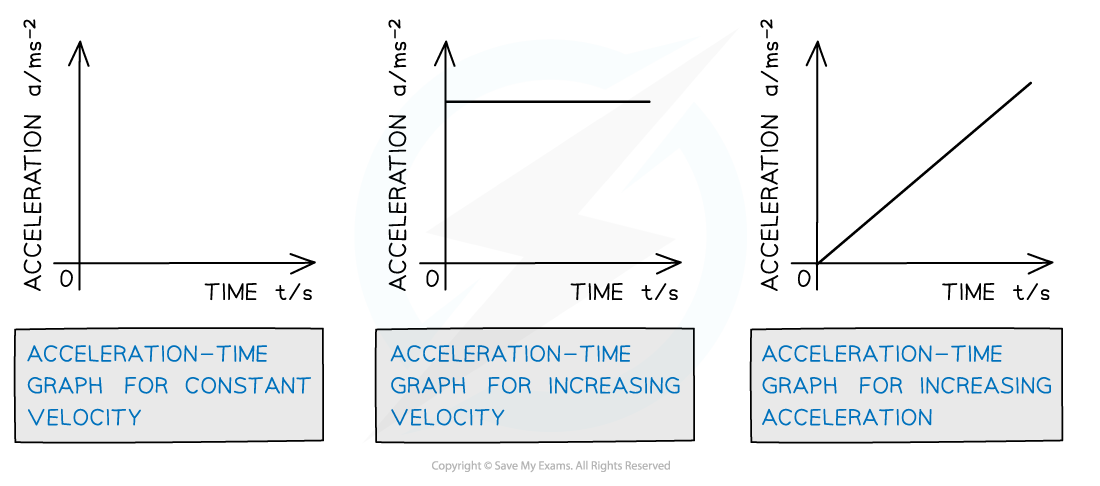
How displacement, velocity and acceleration graphs relate to each other
Worked Example
Tora is training for a cycling tournament.
The velocity-time graph below shows her motion as she cycles along a flat, straight road.
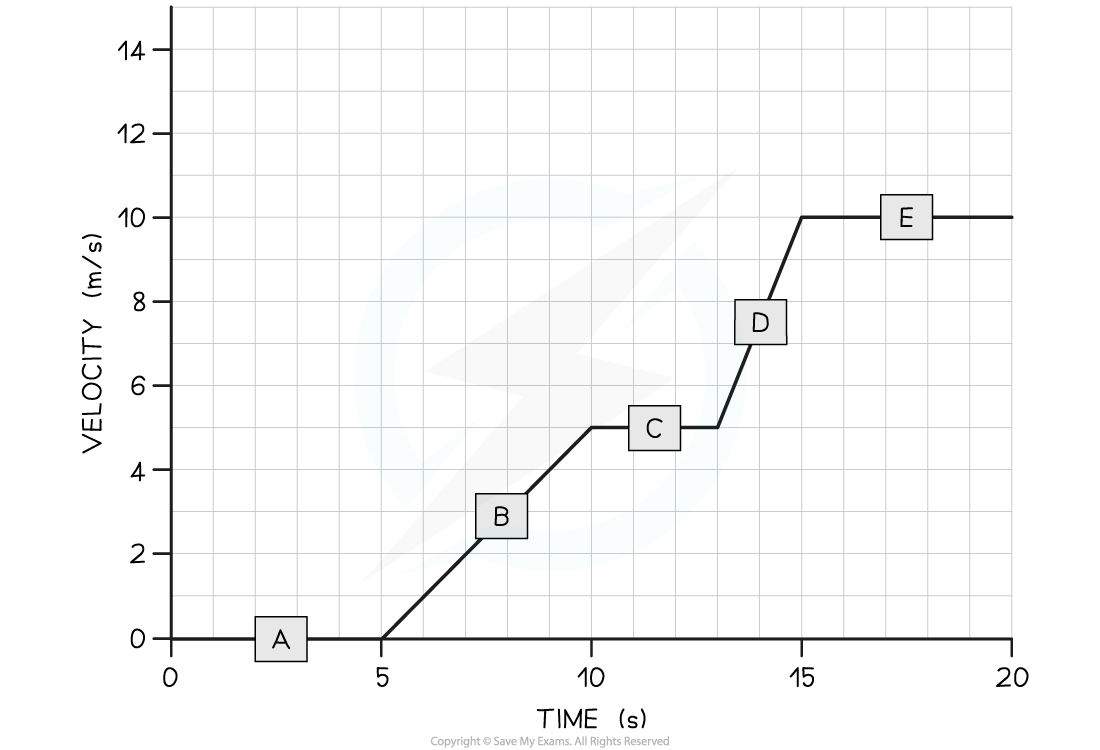
(a) In which section (A, B, C, D, or E) of the velocity-time graph is Tora’s acceleration the largest?(b) Calculate Tora’s acceleration between 5 and 10 seconds.
Part (a)
Step 1: Recall that the slope of a velocity-time graph represents the magnitude of acceleration
-
-
- The slope of a velocity-time graph indicates the magnitude of accelerationTherefore, the only sections of the graph where Tora is accelerating is section B and section D
- Sections A, C, and E are flat – in other words, Tora is moving at a constant velocity (i.e. not accelerating)
-
Step 2: Identify the section with the steepest slope
-
-
- Section D of the graph has the steepest slope
- Hence, the largest acceleration is shown in section D
-
Part (b)
Step 1: Recall that the gradient of a velocity-time graph gives the acceleration
-
-
- Calculating the gradient of a slope on a velocity-time graph gives the acceleration for that time period
-
Step 2: Draw a large gradient triangle at the appropriate section of the graph
-
-
- A gradient triangle is drawn for the time period between 5 and 10 seconds below:
-
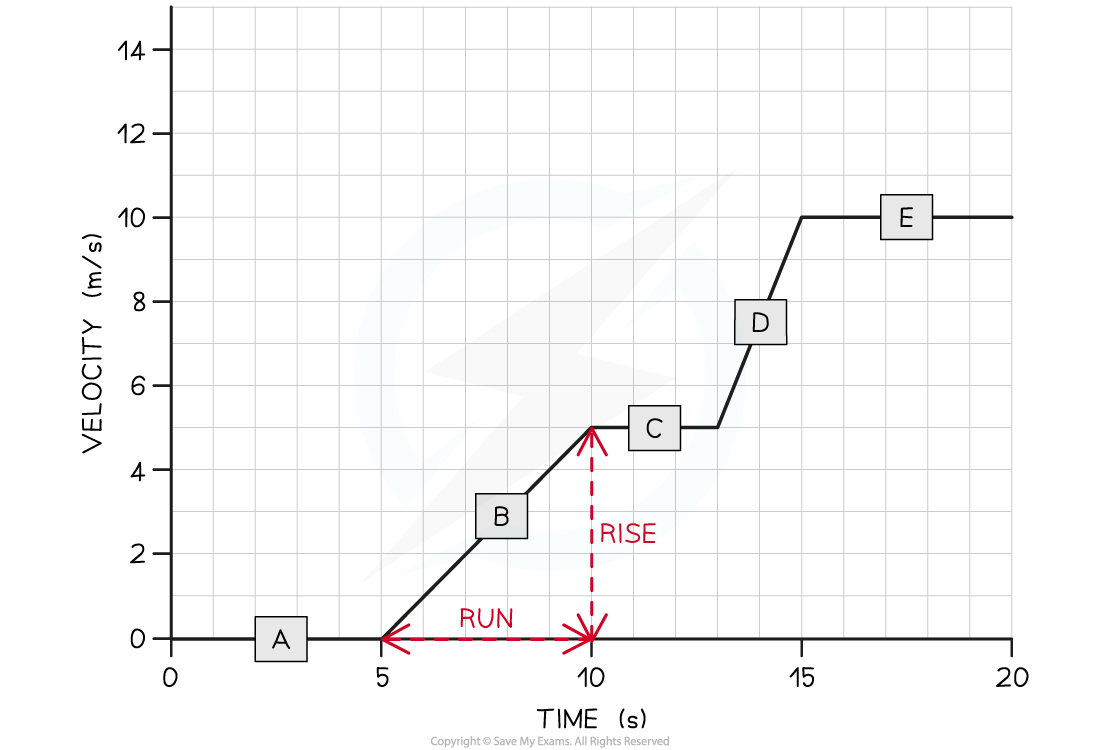
Step 3: Calculate the size of the gradient and state this as the acceleration
-
-
- The acceleration is given by the gradient, which can be calculated using:
-
acceleration = gradient = 5 ÷ 5 = 1 m/s2
-
-
- Therefore, Tora accelerated at 1 m/s2 between 5 and 10 seconds
-
Motion of a Bouncing Ball
- For a bouncing ball, the acceleration due to gravity is always in the same direction (in a uniform gravitational field such as the Earth's surface)
- This is assuming there are no other forces on the ball, such as air resistance
- Since the ball changes its direction when it reaches its highest and lowest point, the direction of the velocity will change at these points
- The vector nature of velocity means the ball will sometimes have a:
- Positive velocity if it is traveling in the positive direction
- Negative velocity if it is traveling in the negative direction
- An example could be a ball bouncing from the ground back upwards and back down again
- The positive direction is taken as upwards
- This will be either stated in the question or can be chosen, as long as the direction is consistent throughout
- Ignoring the effect of air resistance, the ball will reach the same height every time before bouncing from the ground again
- When the ball is traveling upwards, it has a positive velocity which slowly decreases (decelerates) until it reaches its highest point
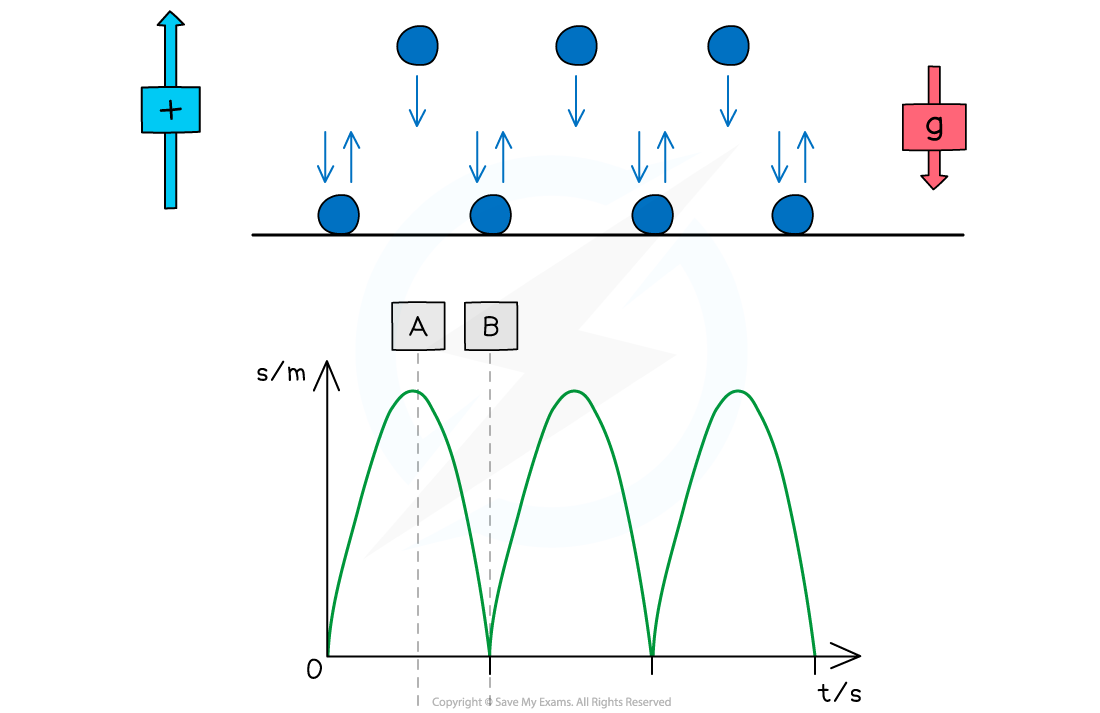
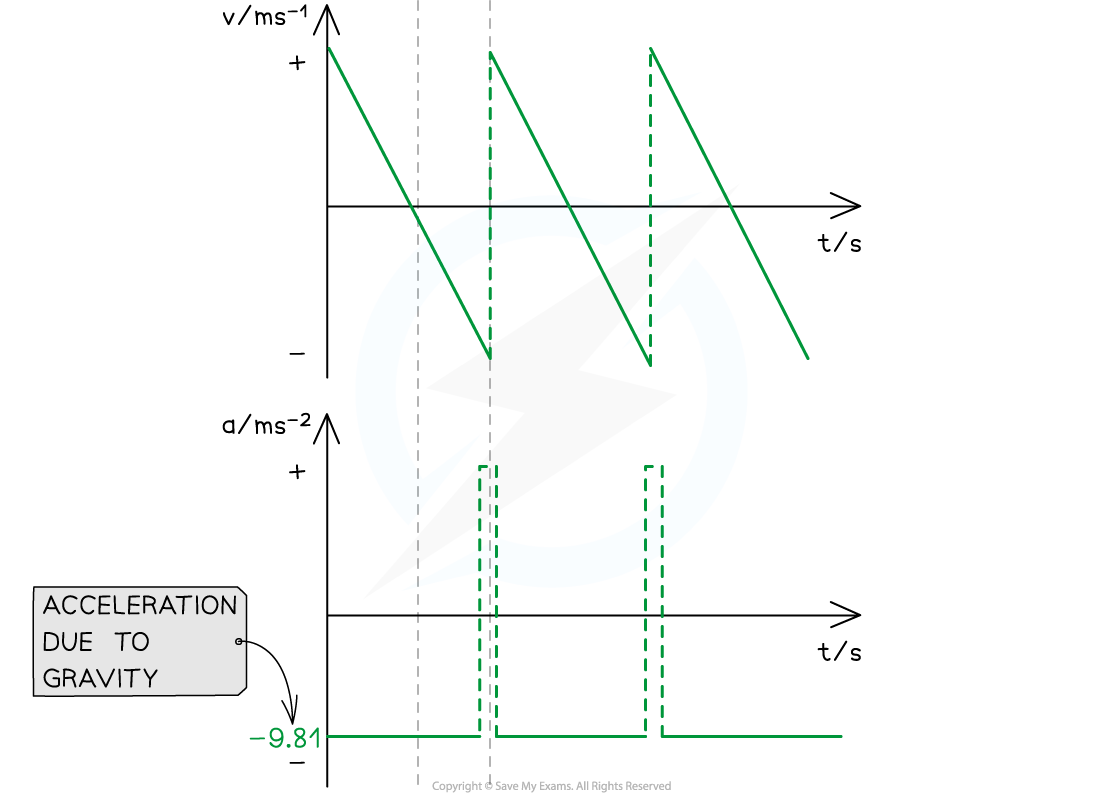
- At point A (the highest point):
- The ball is at its maximum displacement
- The ball momentarily has zero velocity
- The velocity changes from positive to negative as the ball changes direction
- The acceleration, g, is still constant and directed vertically downwards
- At point B (the lowest point):
- The ball is at its minimum displacement (on the ground)
- Its velocity changes instantaneously from negative to positive, but its speed (magnitude) remains the same
- The change in direction causes a momentary acceleration (since acceleration = change in velocity / time)
Worked Example
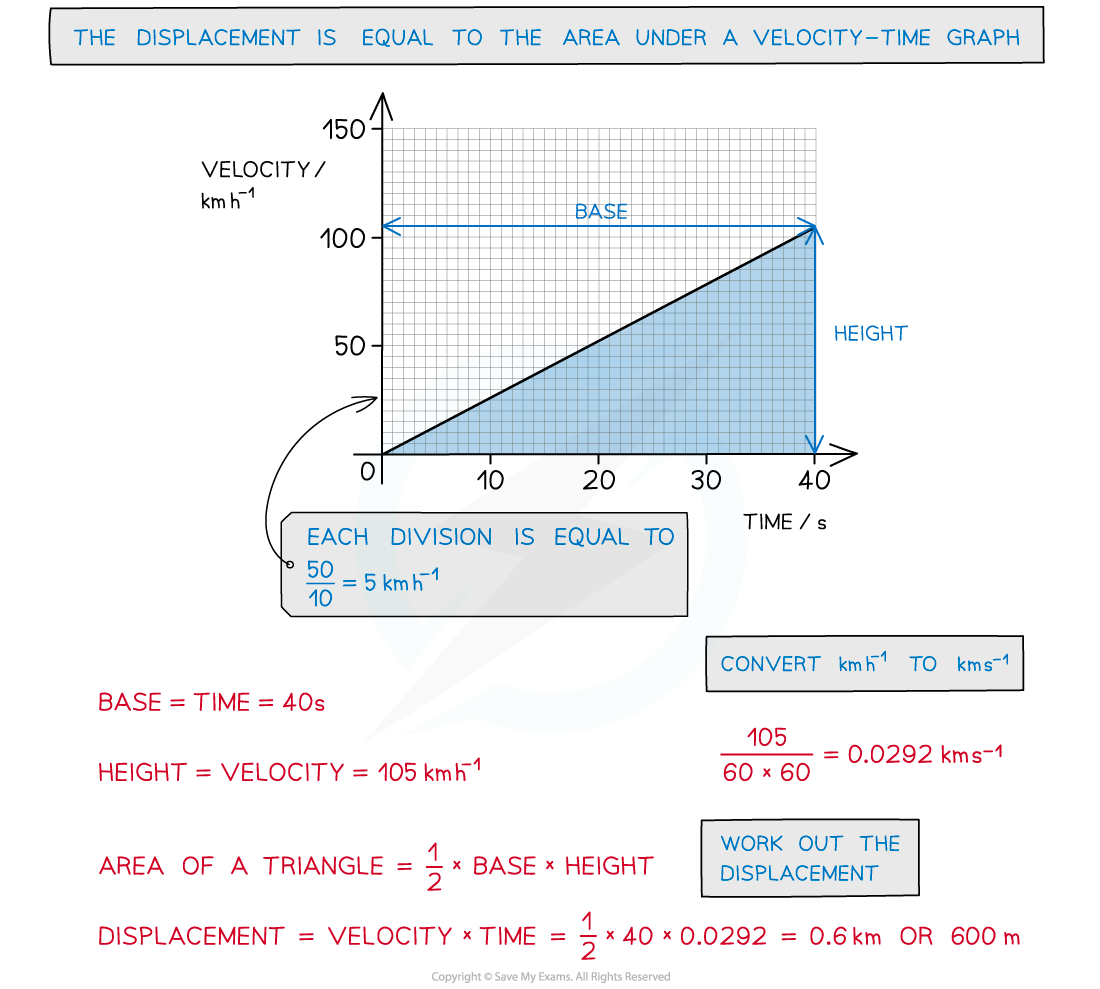
The velocity-time graph of a vehicle travelling with uniform acceleration is shown in the diagram below.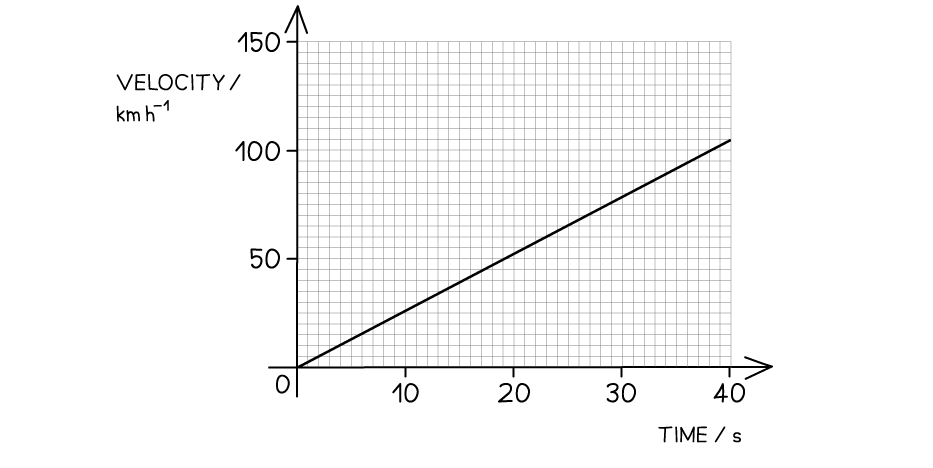 Calculate the displacement of the vehicle at 40 s.
Calculate the displacement of the vehicle at 40 s.
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





