- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: SL复习笔记1.2.1 Random & Systematic Errors
Random & Systematic Errors
- Measurements of quantities are made with the aim of finding the true value of that quantity
- In reality, it is impossible to obtain the true value of any quantity as there will always be a degree of uncertainty
- The uncertainty is an estimate of the difference between a measurement reading and the true value
- The two types of measurement errors that lead to uncertainty are:
- Random errors
- Systematic errors
Random Errors
- Random errors cause unpredictable fluctuations in an instrument’s readings as a result of uncontrollable factors, such as environmental conditions
- This affects the precision of the measurements taken, causing a wider spread of results about the mean value
- To reduce random error:
- Repeat measurements several times and calculate an average from them
Systematic Errors
- Systematic errors arise from the use of faulty instruments used or from flaws in the experimental method
- This type of error is repeated consistently every time the instrument is used or the method is followed, which affects the accuracy of all readings obtained
- To reduce systematic errors:
- Instruments should be recalibrated, or different instruments should be used
- Corrections or adjustments should be made to the technique
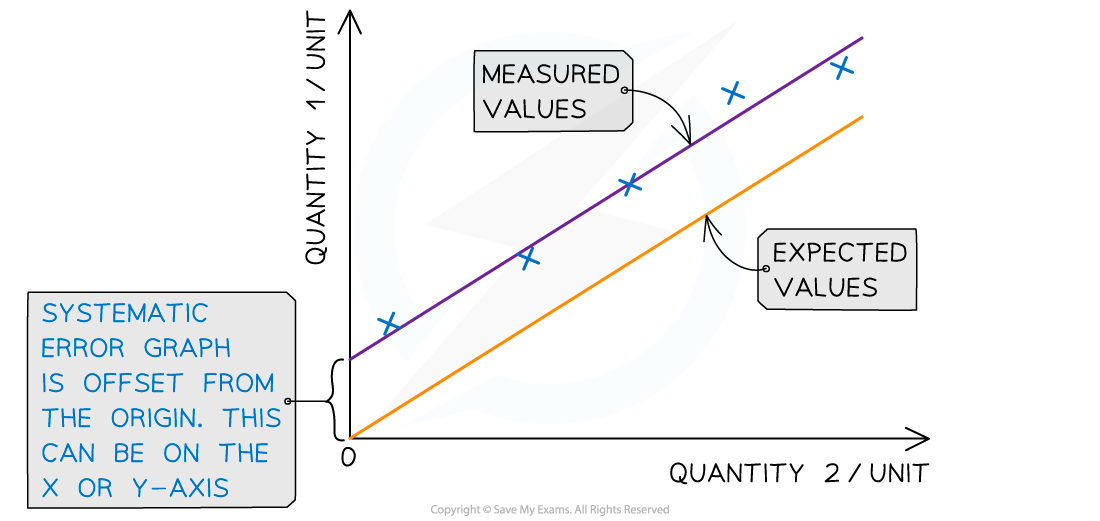
Systematic errors on graphs are shown by the offset of the line from the origin
Zero Errors
- This is a type of systematic error which occurs when an instrument gives a reading when the true reading is zero
- For example, a top-ban balance that starts at 2 g instead of 0 g
- To account for zero errors
- Take the difference of the offset from each value
- For example, if a scale starts at 2 g instead of 0 g, a measurement of 50 g would actually be 50 – 2 = 48 g
- The offset could be positive or negative
Reading Errors
- When measuring a quantity using an analogue device such as a ruler, the uncertainty in that measured quantity is ±0.5 the smallest measuring interval
- When measuring a quantity using a digital device such as a digital scale or stopwatch, the uncertainty in that measured quantity is ±1 the smallest measuring interval
- To reduce reading errors:
- Use a more precise device with smaller measuring intervals and therefore less uncertainty
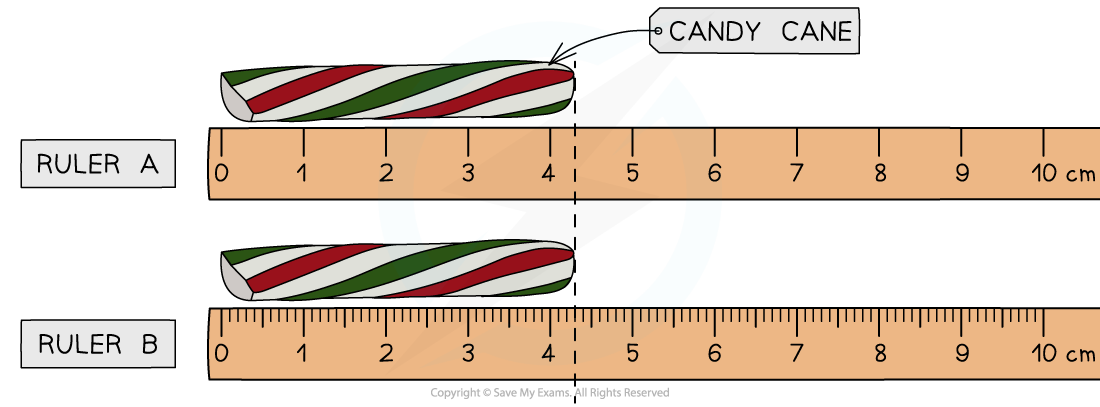
Both rulers measure the same candy cane, yet Ruler B is more precise than Ruler A due to smaller interval size
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





