- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Chemistry: SL复习笔记1.2.4 The Ideal Gas Equation
Ideal Gas Equation
Kinetic theory of gases
- The kinetic theory of gases states that molecules in gases are constantly moving
- The theory makes the following assumptions:
- The gas molecules are moving very fast and randomly
- The molecules hardly have any volume
- The gas molecules do not attract or repel each other (no intermolecular forces)
- No kinetic energy is lost when the gas molecules collide with each other (elastic collisions)
- The temperature of the gas is directly proportional to the average kinetic energy of the molecules
- Gases that follow the kinetic theory of gases are called ideal gases
- However, in reality gases do not fit this description exactly but may come very close and are called real gases
- The volume that a gas occupies depends on:
- Its pressure
- Its temperature
Ideal gas equation
- The ideal gas equation shows the relationship between pressure, volume, temperature and number of moles of gas of an ideal gas:
PV = nRT
P = pressure (pascals, Pa)
V = volume (m3)
n = number of moles of gas (mol)
R = gas constant (8.31 J K-1 mol-1)
T = temperature (Kelvin, K)
- The ideal gas equation can also be used to calculate the molar mass (M) of a gas
Worked Example
Calculate the volume, in dm3, occupied by 0.781 mol of oxygen at a pressure of 220 kPa and a temperature of 21 °C.
Answer:
Step 1: Rearrange the ideal gas equation to find volume of the gas
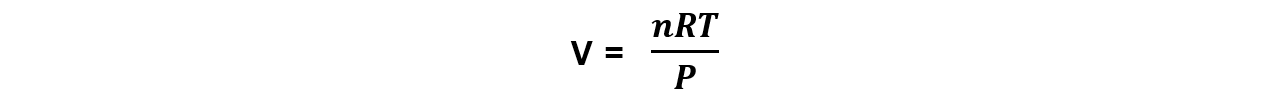 Step 2: Convert into the correct units and calculate the volume the oxygen gas occupies
Step 2: Convert into the correct units and calculate the volume the oxygen gas occupies
p = 220 kPa = 220 000 Pa
n = 0.781 mol
R = 8.31 J K-1 mol-1
T = 21 oC = 294 K
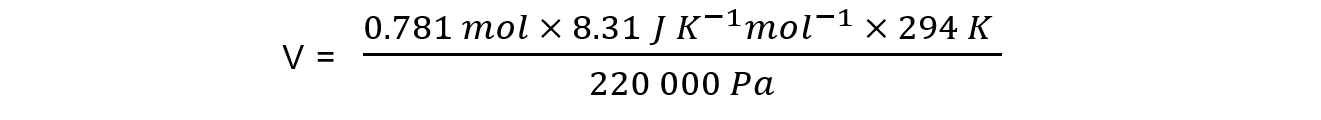
= 0.00867 m3
= 8.67 dm3
Exam Tip
A word about units...Students often mess up gas calculations by getting their unit conversions wrong, particularly from cm3 to m3. Think about what a cubic metre actually is - a cube with sides 1 m or 100 cm long.The volume of this cube is 100 x 100 x 100 = 1 000 000 or 106 cm3So when you convert from m3 to cm3 you MULTIPLY by 106 and when you convert from cm3 to m3 you DIVIDE by 106 (or multiply by 10-6 which is the same thing)
Worked Example
Calculate the pressure of a gas, in kPa, given that 0.20 moles of the gas occupy 10.1 dm3 at a temperature of 25 oC.
Answer:
Step 1: Rearrange the ideal gas equation to find the pressure of the gas
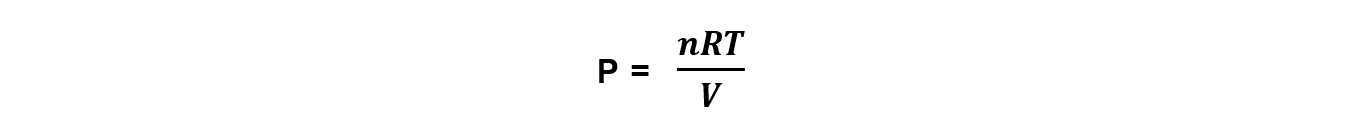 Step 2: Convert to the correct units and calculate the pressure
Step 2: Convert to the correct units and calculate the pressure
n = 0.20 mol
V = 10.1 dm3 = 0.0101 m3 = 10.1 x 10-3 m3
R = 8.31 J K-1 mol-1
T = 25 oC = 298 K
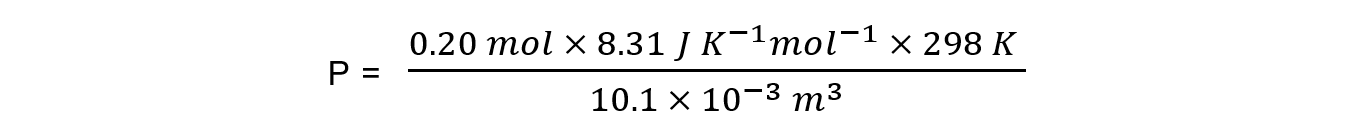 P = 49 037 Pa = 49 kPa (2 sig figs)
P = 49 037 Pa = 49 kPa (2 sig figs)
Worked Example
Calculate the temperature of a gas, in oC, if 0.047 moles of the gas occupy 1.2 dm3 at a pressure of 100 kPa.
Answer:
Step 1: Rearrange the ideal gas equation to find the temperature of the gas
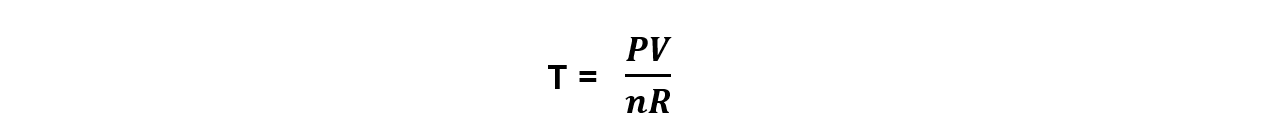 Step 2: Convert to the correct units and calculate the pressure
Step 2: Convert to the correct units and calculate the pressure
n = 0.047 mol
V = 1.2 dm3 = 0.0012 m3 = 1.2 x 10-3 m3
R = 8.31 J K-1 mol-1
P = 100 kPa = 100 000 Pa
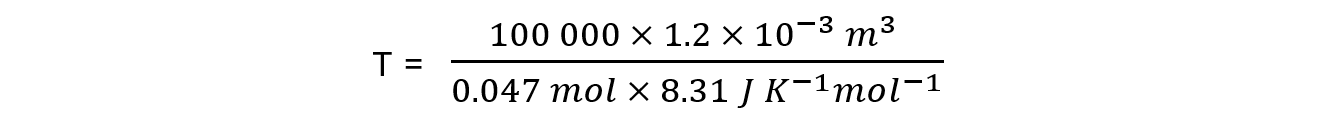 T = 307.24 K = 34.24 oC= 34 oC (2 sig figs)
T = 307.24 K = 34.24 oC= 34 oC (2 sig figs)
Worked Example
A flask of volume 1000 cm3 contains 6.39 g of a gas. The pressure in the flask was 300 kPa and the temperature was 23 °C.Calculate the molar mass of the gas.
Answer:
Step 1: Rearrange the ideal gas equation to find the number of moles of gas
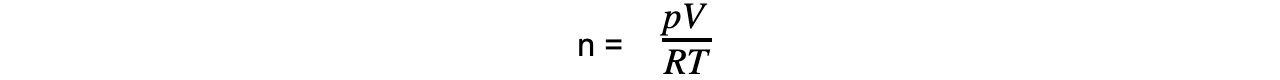
Step 2: Convert to the correct units and calculate the number of moles of gas
P = 300 kPa = 300 000 Pa
V = 1000 cm3 = 0.001 m3 = 1.0 x 10-3 m3
R = 8.31 J K-1 mol-1
T = 23 oC = 296 K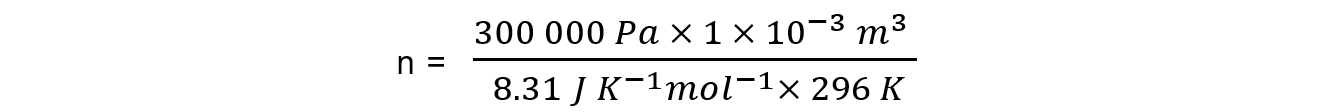
n = 0.12 mol
Step 3: Calculate the molar mass using the number of moles of gas
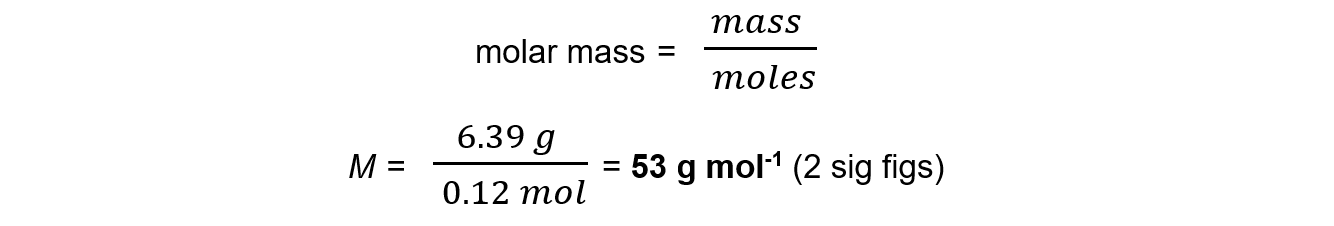
Exam Tip
To calculate the temperature in Kelvin, add 273 to the Celsius temperature, eg. 100 oC is 373 Kelvin.
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





