IB DP Physics: HL复习笔记12.2.7 Measuring Half-Life

IB, 学科真题, 教材/笔记, 福利干货 8月 2, 2022

Measuring Half-Life

  • Half-life is defined as:

The time taken for the initial number of nuclei to halve for a particular isotope

  • This means when a time equal to the half-life has passed, the activity of the sample will also half
  • This is because the activity is proportional to the number of undecayed nuclei, A ∝ N

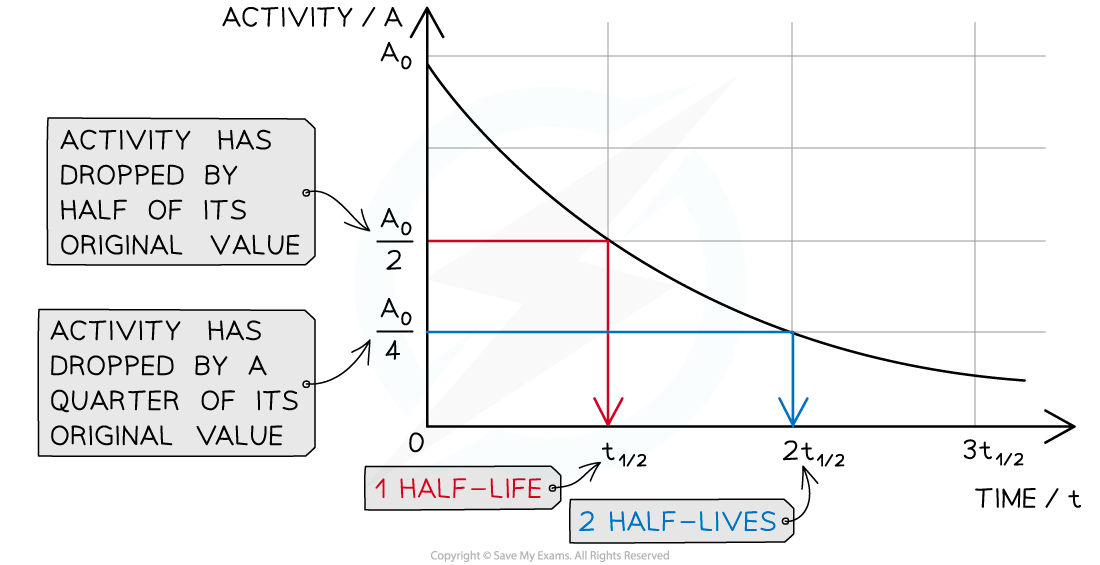
6.2.10-Half-life-Graph

When a time equal to the half-life passes, the activity falls by half, when two half-lives pass, the activity falls by another half (which is a quarter of the initial value)

  • To find an expression for half-life, start with the equation for exponential decay:

N = N0 e–λt

  • Where:
    • N = number of nuclei remaining in a sample
    • N0 = the initial number of undecayed nuclei (when t = 0)
    • λ = decay constant (s-1)
    • t = time interval (s)
  • When time t is equal to the half-life t½, the activity N of the sample will be half of its original value, so N = ½ N0

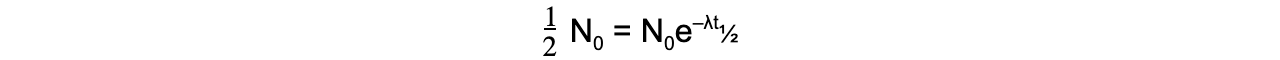
5.-Calculating-Half-Life-equation-1

  • The formula can then be derived as follows:

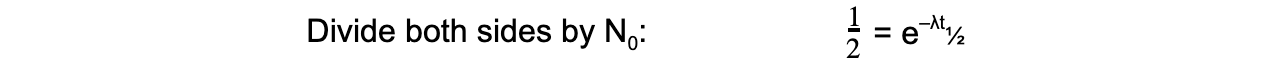
5.-Calculating-Half-Life-equation-2

5.-Calculating-Half-Life-equation-3

5.-Calculating-Half-Life-equation-3a

  • Therefore, half-life t½ can be calculated using the equation:

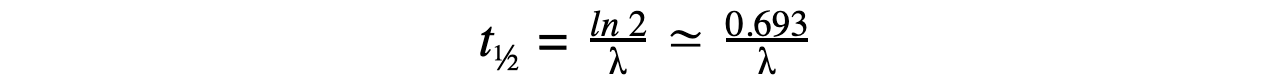
5.-Calculating-Half-Life-equation-4

  • This equation shows that half-life t½ and the radioactive decay rate constant λ are inversely proportional
    • Therefore, the shorter the half-life, the larger the decay constant and the faster the decay
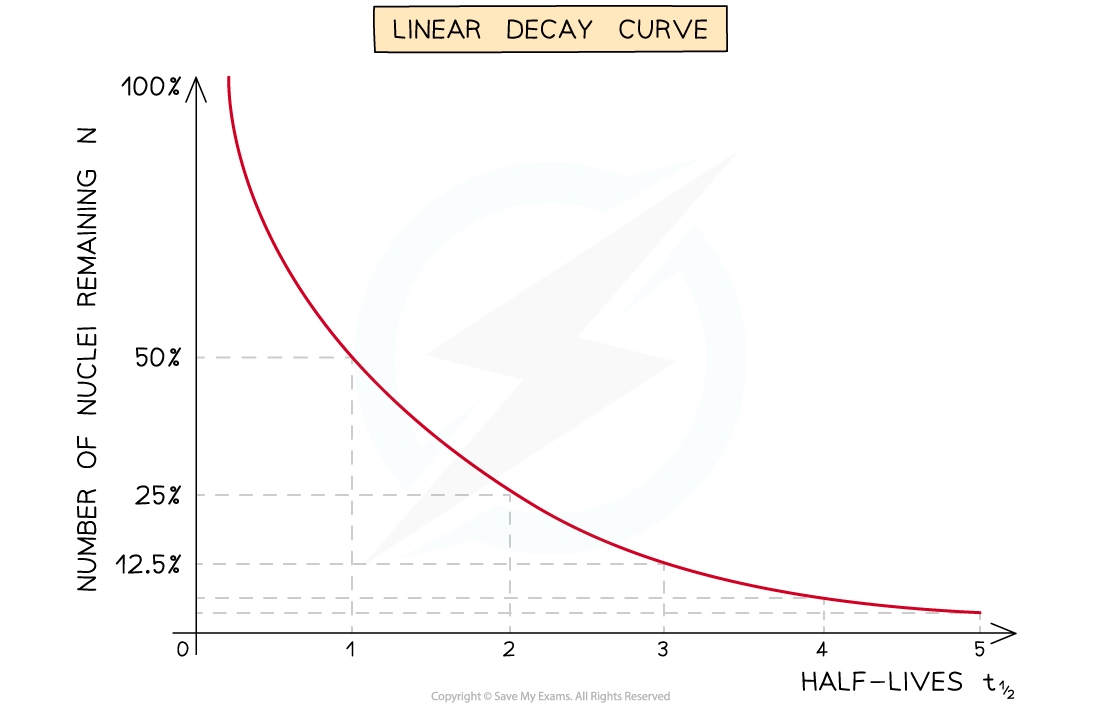
  • The half-life of a radioactive substance can be determined from decay curves and log graphs
  • Since half-life is the time taken for the initial number of nuclei, or activity, to reduce by half, it can be found by
    • Drawing a line to the curve at the point where the activity has dropped to half of its original value
    • Drawing a line from the curve to the time axis, this is the half-life

8.2.3-Half-Life-Decay-Curves-1

Measuring Long Half-Lives

  • For nuclides with long half-lives, on the scale of years, this can be measured by:
    • Measuring the mass of the nuclide in a pure sample
    • Determining the number of atoms N in the sample using N = nNA
    • Measuring the total activity A of the sample using the counts collected by a detector
    • Note: The sample must be sufficiently large enough in order for a significant number of decays to occur per unit time so that an accurate measure of activity can be made

Measuring Short Half-Lives

  • For nuclides with short half-lives, on the scale of seconds, hours or days, this can be measured by:
    • Measuring the background count rate in the laboratory (to subtract from each reading)
    • Taking readings of the count rate against time until the value equals that of the background count rate (i.e. until all of the sample has decayed)
    • Plotting a graph of activity, A, against time, t (as corrected count rate ∝ activity, A)
    • Making at least 3 estimates of half-life from the graph and taking a mean

OR

    • Plotting a graph of ln N against time, t (as corrected count rate ∝ number of nuclei in the sample, N)
    • Finding the gradient of this graph, which gives –λ
    • Straight-line graphs tend to be more useful than curves for interpreting data
    • Due to the exponential nature of radioactive decay logarithms can be used to achieve a straight line graph
  • Take the exponential decay equation for the number of nuclei

N = N0 e–λt

  • Taking the natural logs of both sides

ln N = ln (N0) − λt

  • In this form, this equation can be compared to the equation of a straight line

y = mx + c

  • Where:
    • ln (N) is plotted on the y-axis
    • t is plotted on the x-axis
    • gradient = −λ
    • y-intercept = ln (N0)
  • Half-lives can be found in a similar way to the decay curve but the intervals will be regular as shown below:

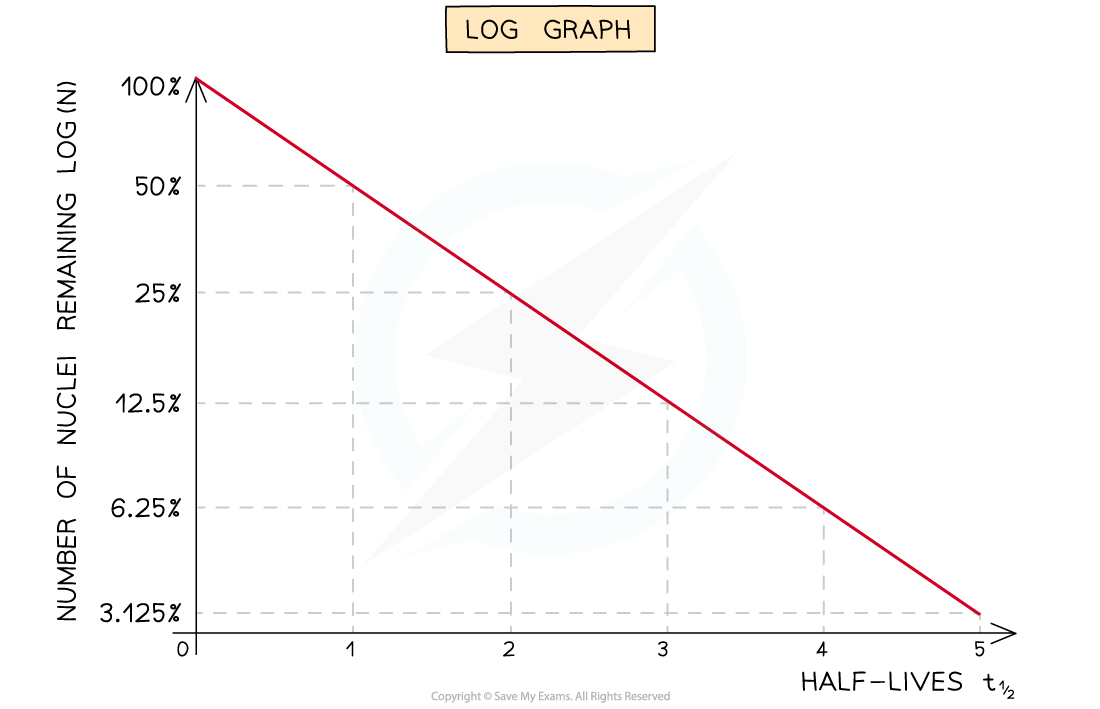
8.2.3-Half-Life-Decay-Curves-2

A logarithmic graph. This represents the relationship: