- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: HL复习笔记12.2.4 Nuclear Energy Levels
Nuclear Energy Levels
- In the same way that electrons can exist in excited states, nuclei can also exist in excited states
- After an unstable nucleus emits an alpha particle, beta particle or undergoes electron capture, it may emit any remaining energy in the form of a gamma photon (γ)
- Emission of a γ photon does not change the number of protons or neutrons in the nucleus, it only allows the nucleus to lose energy
- This happens when a daughter nucleus is in an excited state after a decay
- This excited state is usually very short-lived, and the nucleus quickly moves to its ground state, either directly or via one or more lower-energy excited states
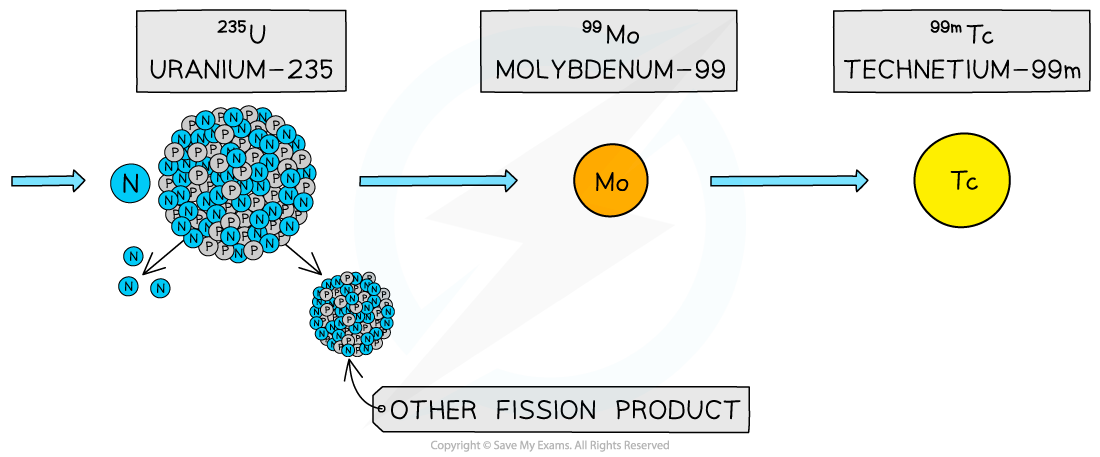
- One common application of this is the use of technetium-99m as a γ source in medical diagnosis
- The ‘m’ stands for metastable which means the nucleus exists in a particularly stable excited state
- Technetium-99m is the decay product of molybdenum-99, which can be found as a product in nuclear reactors
- The decay of molybdenum-99 is shown below:
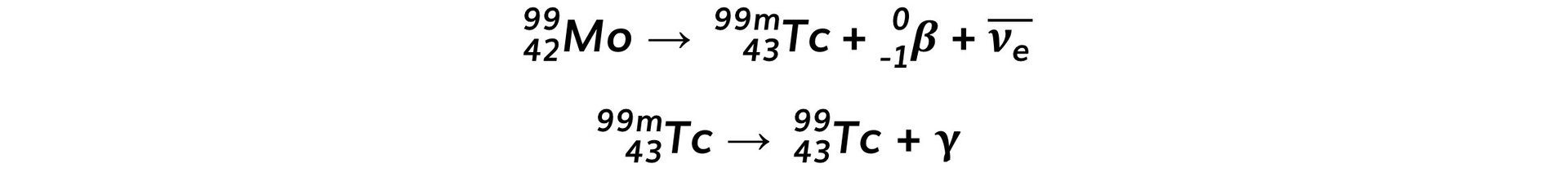
- The half-life of molybdenum-99 is 66 hours
- This is long enough for the sample to be transported to hospitals
- Subsequently, the technetium-99m can be separated at the hospital
- Technetium-99m has a short half-life of 6 hours
- This is an adequate timeframe for examining a patient
- Plus, it is short enough to minimise damage to the patient
Nuclear Energy Level Diagrams
- Nuclear energy levels are similar to electron energy levels
- The nuclear energy level diagram of molybdenum-99 can be represented as follows:
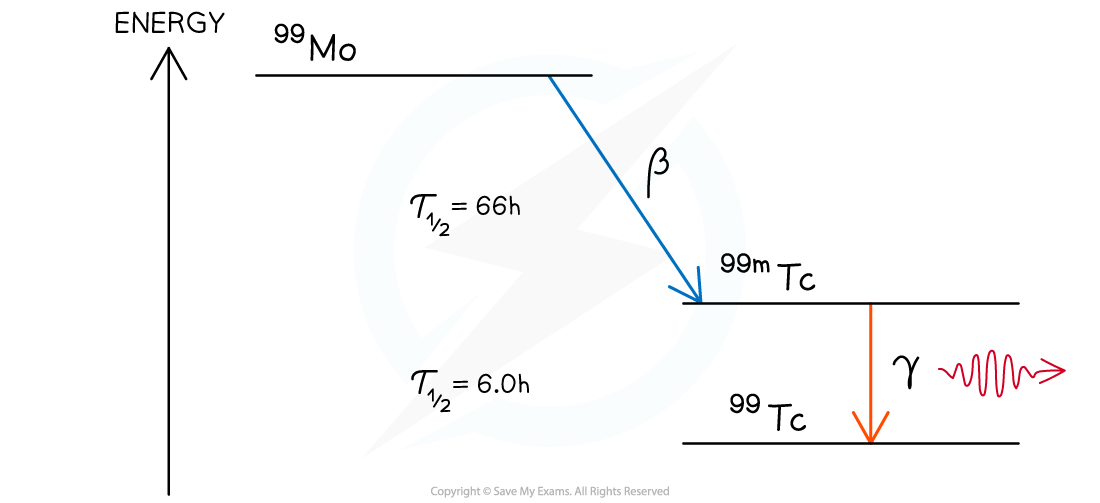
- The decay mode (usually alpha or beta) is represented by a diagonal line
- The excited state, or states, are generally stacked in descending energy order to the right of the decay
Worked Example
A nucleus of iron Fe-59 decays into a stable nucleus of cobalt Co-59. It decays by β– emission followed by the emission of γ-radiation as the Co-59 nucleus de-excites into its ground state.
The total energy released when the Fe-59 nucleus decays is 2.52 × 10–13 J. The Fe-59 nucleus can decay to one of three excited states of the cobalt-59 nucleus as shown below. The energies of the excited states are shown relative to the ground state.

Following the production of excited states of Co-59, γ-radiation of discrete wavelengths is emitted.
(a) Calculate the maximum possible kinetic energy of the β– particle emitted in MeV
(b) State the maximum number of discrete wavelengths that could be emitted
(c) Calculate the longest wavelength of the emitted γ-radiation
Part (a)
Step 1: Identify the beta emission with the largest energy gap

Step 2: Calculate the energy difference
ΔE = (2.52 – 1.76) × 10–13 = 7.6 × 10–14 J
Step 3: Convert from J to MeV
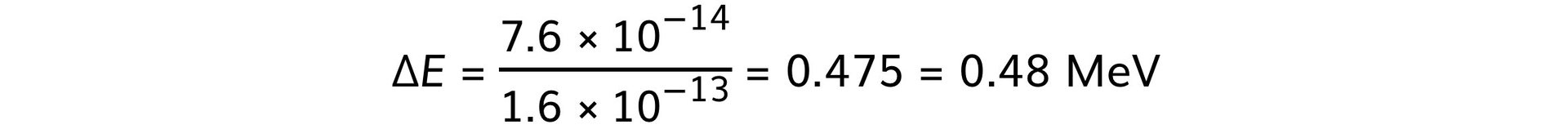
-
- 1 MeV = 1.6 × 10–13 J
Part (b)

-
- There are 6 possible transitions, hence 6 discrete wavelengths could be emitted
Part (c)
Step 1: Identify the emission with the longest wavelength / smallest energy gap

-
- Longest wavelength = lowest frequency = smallest energy
Step 2: Calculate the energy difference
ΔE = (2.29 – 2.06) × 10–13 = 2.3 × 10–14 J
Step 3: Write down de Broglie’s wavelength equation
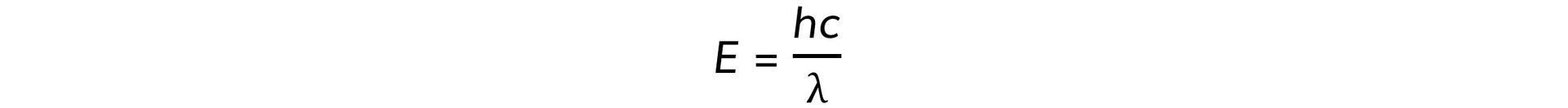
Where:
-
- h = Planck’s constant
- c = speed of light
Step 4: Calculate the wavelength associated with the energy change
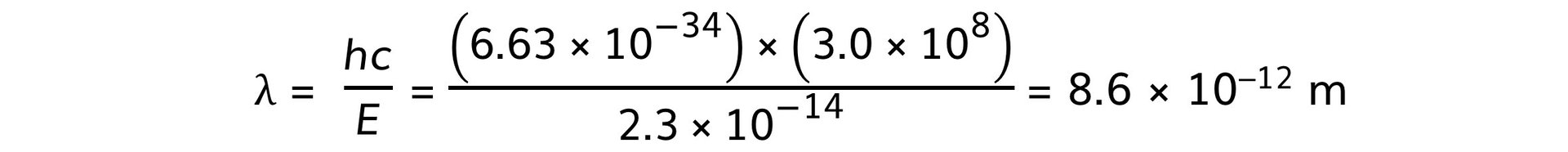
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





