- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: HL复习笔记12.2.2 Nuclear Scattering
Nuclear Scattering
- Electrons accelerated to close to the speed of light have wave-like properties such as the ability to diffract and have a de Broglie wavelength equal to:
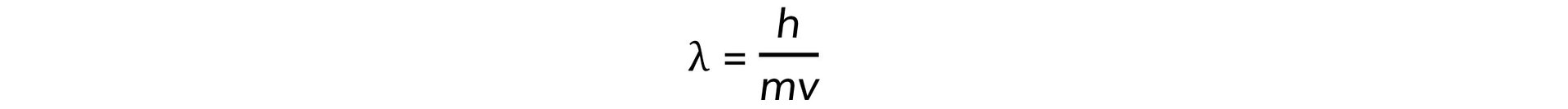
- Where:
- h = Planck's constant
- m = mass of an electron (kg)
- v = speed of the electrons (m s−1)
- When beams of neutrons or electrons are directed at a nucleus they will diffract around it
- The pattern formed by this diffraction has a predictable minimum which forms at an angle θ to the original direction according to the equation
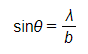
- The diffraction pattern forms a central bright spot with dimmer concentric circles around it
- From this pattern, a graph of intensity against diffraction angle can be used to find the diffraction angle of the first minimum
- The graph of intensity against angle obtained through electron diffraction is as follows:

The first minimum of the intensity-angle graph can be used to determine nuclear radius
- Using this, the size of the atomic nucleus, R, can be determined from:
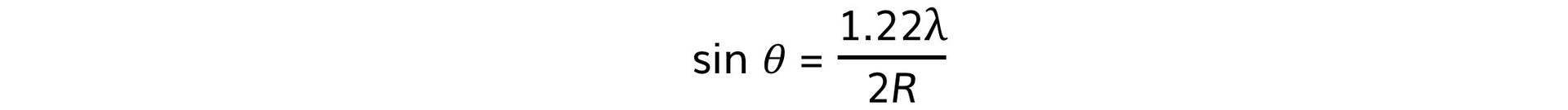
- Where:
- θ = angle of the first minimum (degrees)
- λ = de Broglie wavelength (m)
- R = radius of the nucleus (m)
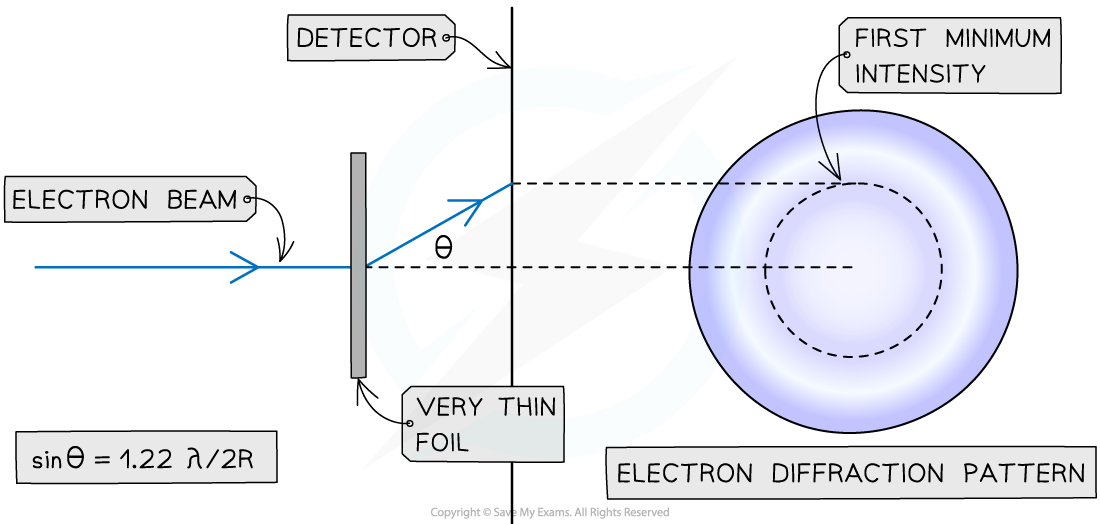
Geometry of electron diffraction
Worked Example
The graph shows how the relative intensity of the scattered electrons varies with angle due to diffraction by the oxygen-16 nuclei. The angle is measured from the original direction of the beam.
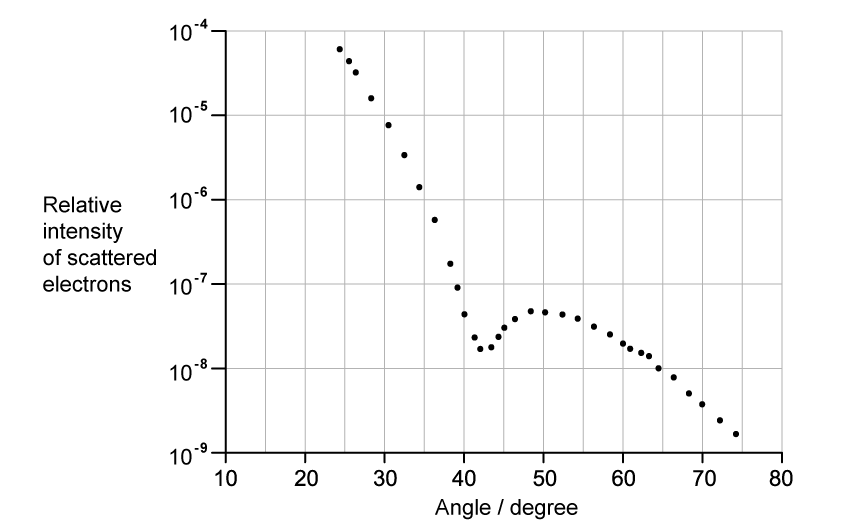
The de Broglie wavelength λ of each electron in the beam is 3.35 × 10−15 m.
Calculate the radius of an oxygen-16 nucleus using information from the graph.
Step 1: Identify the first minimum from the graph
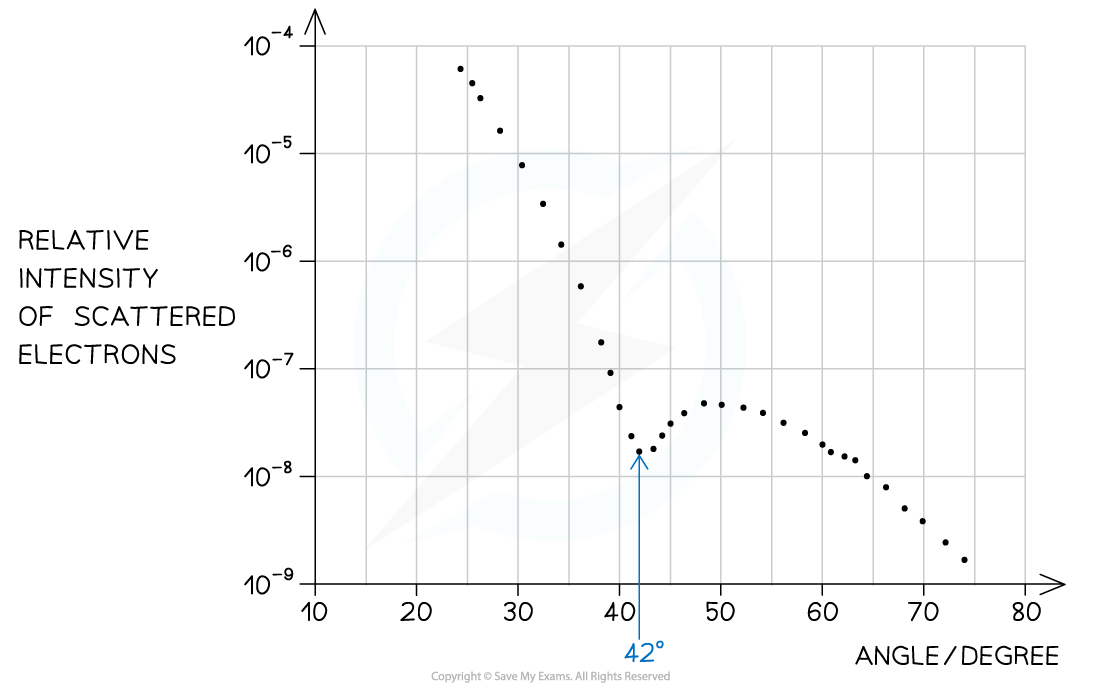
- Angle of first minimum, θ = 42°
Step 2: Write out the equation relating the angle, wavelength, and nuclear radius
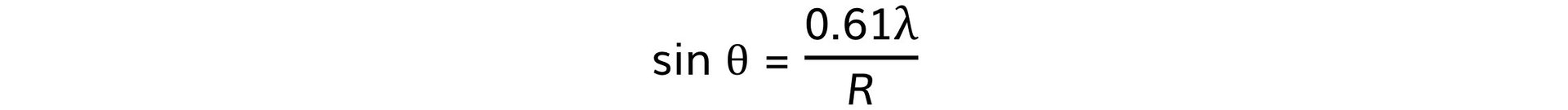
Step 3: Calculate the nuclear radius, R
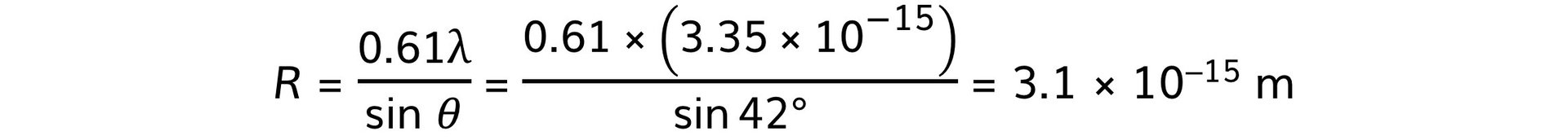
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





