- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: HL复习笔记12.1.10 Tunnelling
Tunnelling
- Single potential wells lead to quantised energy levels and their associated wavefunctions
- The wavefunction extends throughout space
- However, for infinitely deep square wells the wavefunctions are localised within the well region
- The probability of finding the quantum particle at the barrier is zero
- For a finite barrier, the wavefunction can penetrate the barrier
- So, the particle has some probability of being in a “classically forbidden region”
- If there are two well-like regions, the solution of Schrodinger’s equation gives an energy level and wavefunction that extends over the whole region of the potential well
- When the red wave function is squared it gives the probability of finding the particle in a particular region of space
- Since the wave function extends through the barrier this means there is a finite probability of finding the particle in either of the two well regions

A thin barrier or classically forbidden region can result in tunnelling
- Consequently, if a quantum particle were placed in the narrow well on the right, it is possible at some time later to find it in the region on the left
- The particle is said to have tunnelled through the narrow barrier
Tunnelling & Alpha Decay
- The strong nuclear force within the nucleus is represented by the square well
 Nucleons in the nucleus have quantised energy levels and wave functions
Nucleons in the nucleus have quantised energy levels and wave functions
- An alpha particle can gain energy and occupy an excited energy level where the barrier width is smaller
- As a result, the alpha particle can tunnel through the classically forbidden region
- This greatly increases the probability of the alpha particle being emitted
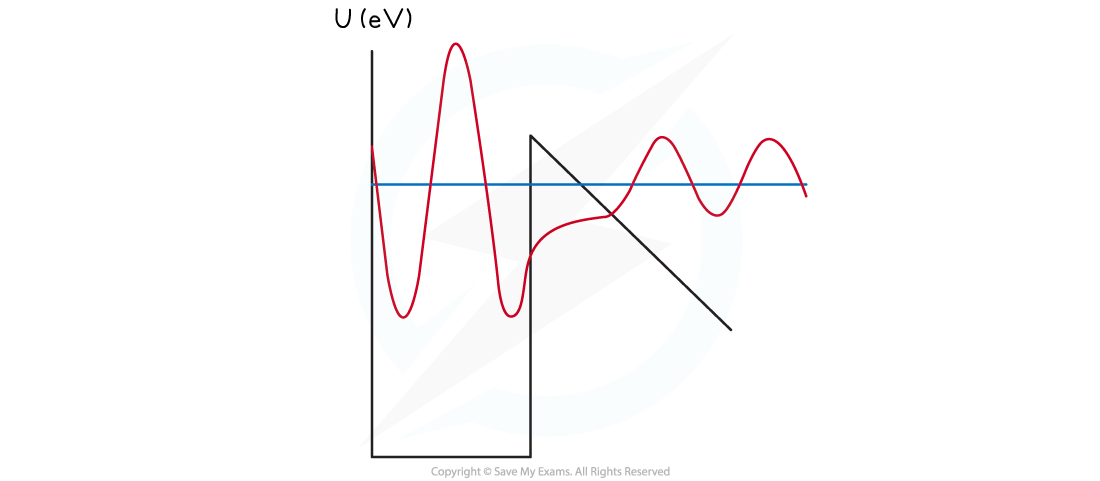
- This greatly increases the probability of the alpha particle being emitted
Alpha decay through quantum mechanical tunnelling
Uses of Quantum Tunnelling
- Quantum tunnelling is utilised in several systems, for example in:
- Semiconductor devices
- Fusion reactions in the Sun
- A scanning tunnelling microscope
- In one mode of operation of a scanning tunnelling microscope, a sharp point, one atom thick, is maintained close to a surface
- This is so that a small tunnelling current between the tip and the surface remains constant
- In this case, the gap between the tip and the sample surface acts as the barrier that the electrons must tunnel through
- The tip is moved up and down and across the surface by piezoelectric transducers allowing the sample surface to be mapped out
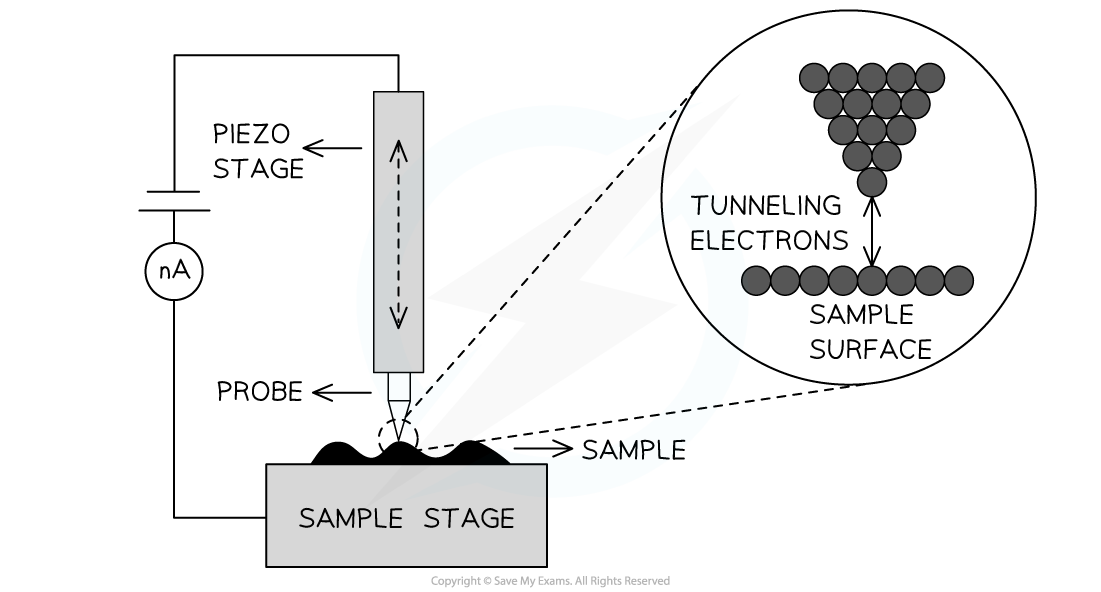
Simplified schematic of a scanning tunnelling microscope
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





