- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: HL复习笔记12.1.9 The Uncertainty Principle
The Uncertainty Principle
- The quantisation of energy levels and their associated wave functions leads to some surprising outcomes
- One of these outcomes is known as the uncertainty principle
- The uncertainty principle states that:
- This leads to two consequences related to:
- Position and momentum
- Energy and time
Position & Momentum
- One example is that it is not possible to know the position and the momentum of a quantum particle precisely
- This can be represented in equation form as:
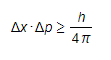 Where:
Where:
- Δx = change in displacement
- Δpx = change in momentum
- h = Planck's constant
- This equation shows that:
- The better the position of the particle is known, the less precise is the knowledge of its momentum
- The value of Planck’s constant is small so this limitation only becomes important for small particles within the quantum regime - it does not apply in the Newtonian mechanics that you have used to calculate momentum for larger objects
Energy & Time
- There is a similar relationship between energy and time where both cannot be known precisely
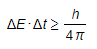 Where:
Where:
- ΔE = change in energy
- Δt = change in time
- h = Planck's constant
Wavefunctions
- This principle can be demonstrated by looking at the wavefunctions associated with quantum particles that are nearly 'free'
- For example, those associated with the energy levels in a 'swimming pool' potential energy well
- The graph of wavefunction vs position shows that while the momentum is known precisely the position of the particle is unknown
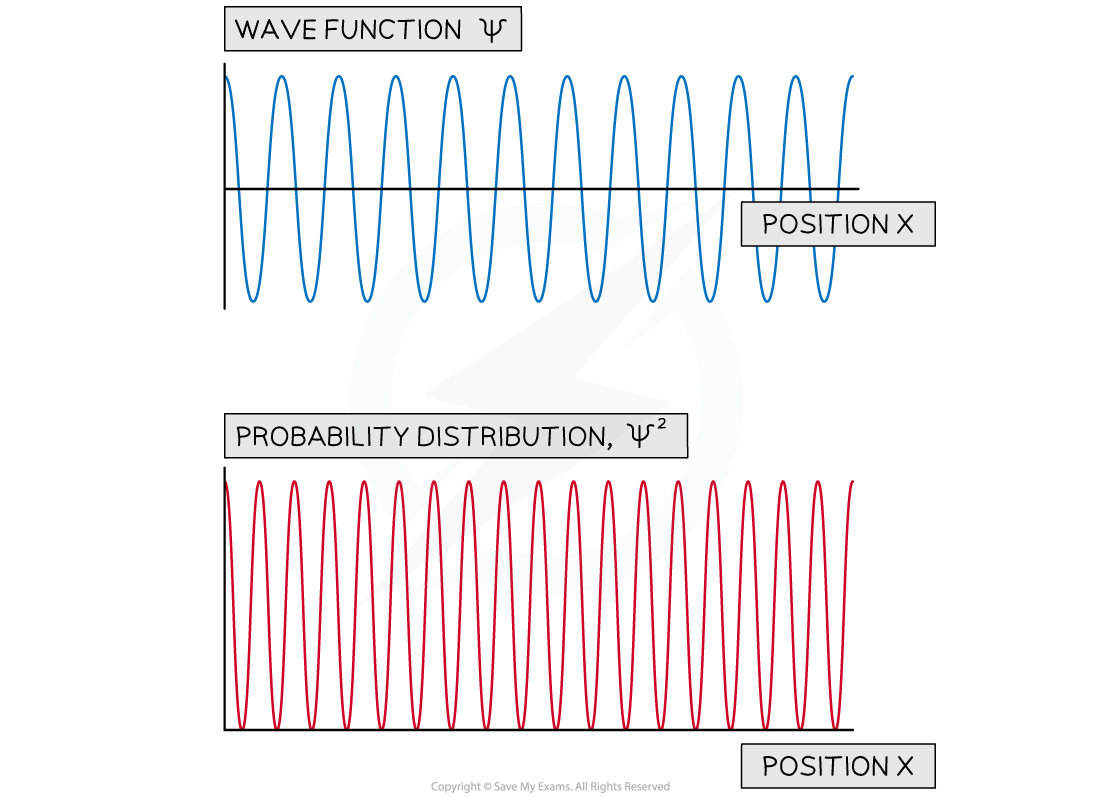
The wave function of a free particle with a fixed energy. The wave function shows it has a single value of momentum while the probability distributions shows that the particle can be anywhere in space.
- For a particle in a 'swimming pool' potential well, its energy levels are close together
- Hence, the wave function can be a mixture of the wavefunctions associated with a number of closely spaced energy levels
- For a range of five neighbouring energy levels, the wavefunction can be obtained by adding the individual wavefunctions
- This is a result of the principle of superposition
- This gives rise to a wave packet, meaning the particle is more likely to be in a particular region of space
- This can be shown by a graph of the probability distribution vs position
- This helps to visualise how the approximate uncertainty in the position, Δx and momentum Δpx can be determined
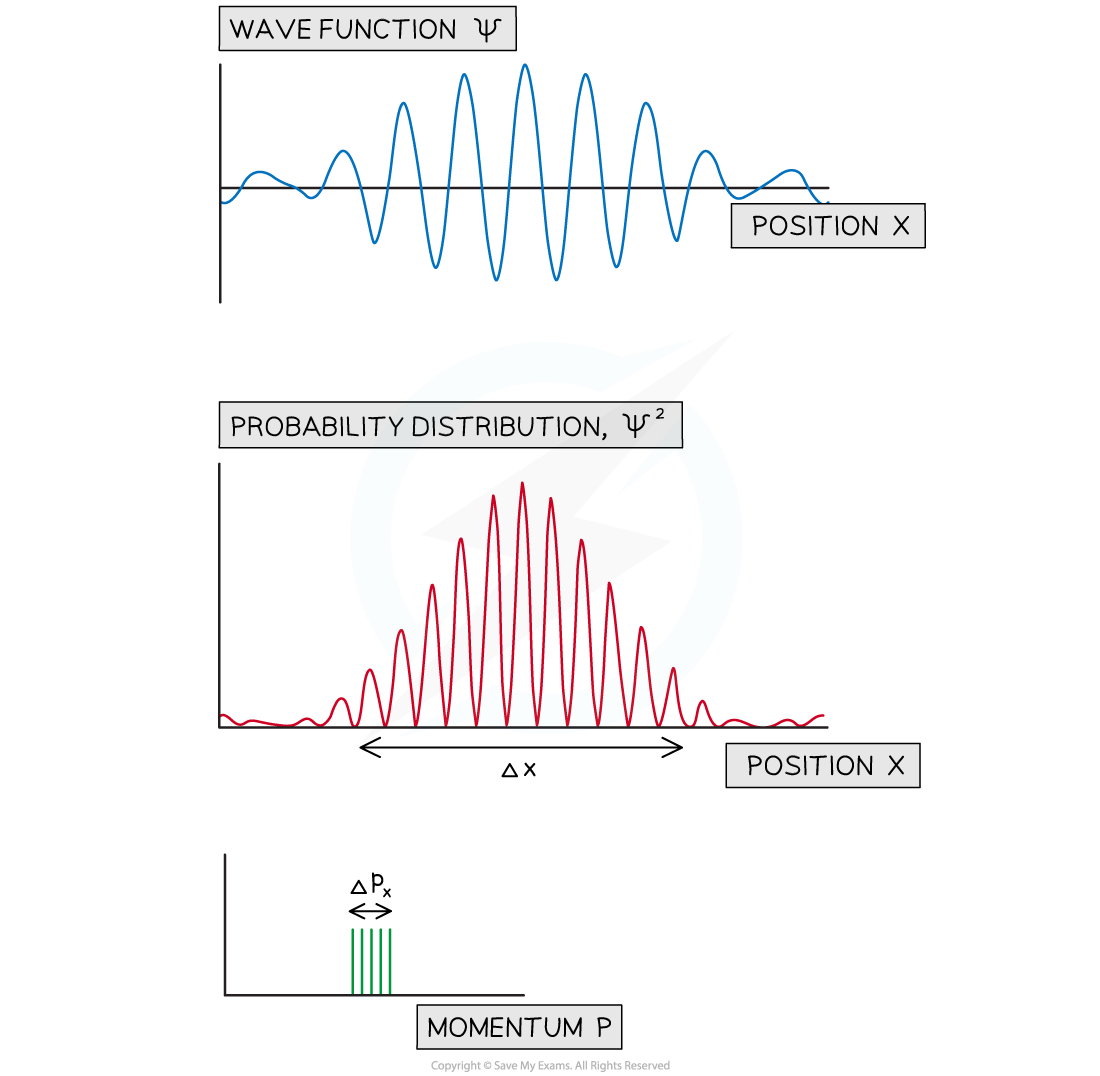
A wave packet made from the wavefunctions associated with five closely spaced energy levels. The probability distribution is shown along with the uncertainty in position and momentum.
- Consider the wavefunctions associated with five and ten energy levels with the probability distribution and the estimates of Δx and Δpx
- Comparing the two sets of graphs, it can be seen that:
- As the momentum becomes less well known the position becomes more well known
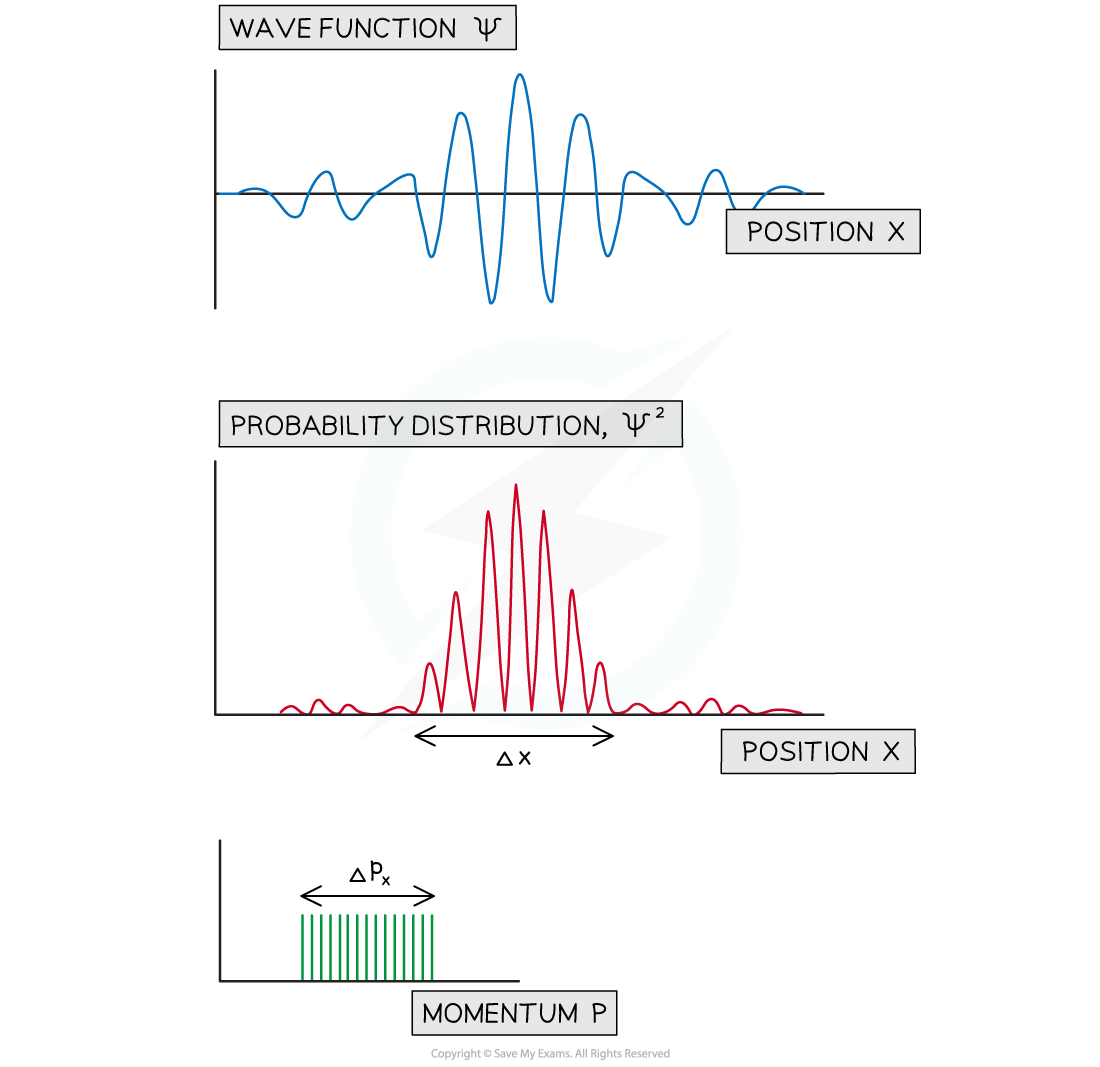
A wave packet made from the wavefunctions associated with five closely spaced energy levels. The probability distribution is shown along with the uncertainty in position and momentum.
Worked Example
A narrow beam of electrons with velocity 106 m s−1 are directed towards a slit which is 10-9 m wide.
The electrons are observed on a screen placed 2.0 m from the slit.
Estimate the length of the area of the screen where electrons will be seen in appreciable numbers.

转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





