The Wave Function
- Bohr showed that the angular momentum of an electron orbiting a hydrogen atom was quantised
- He also showed that the allowed electron energies were also quantised
- Unfortunately, this original model only worked for hydrogen
- Schrodinger then developed an equation that could be used to calculate the quantised energy levels for other atoms
- The only information the equation needs is the shape of the particle’s potential energy function
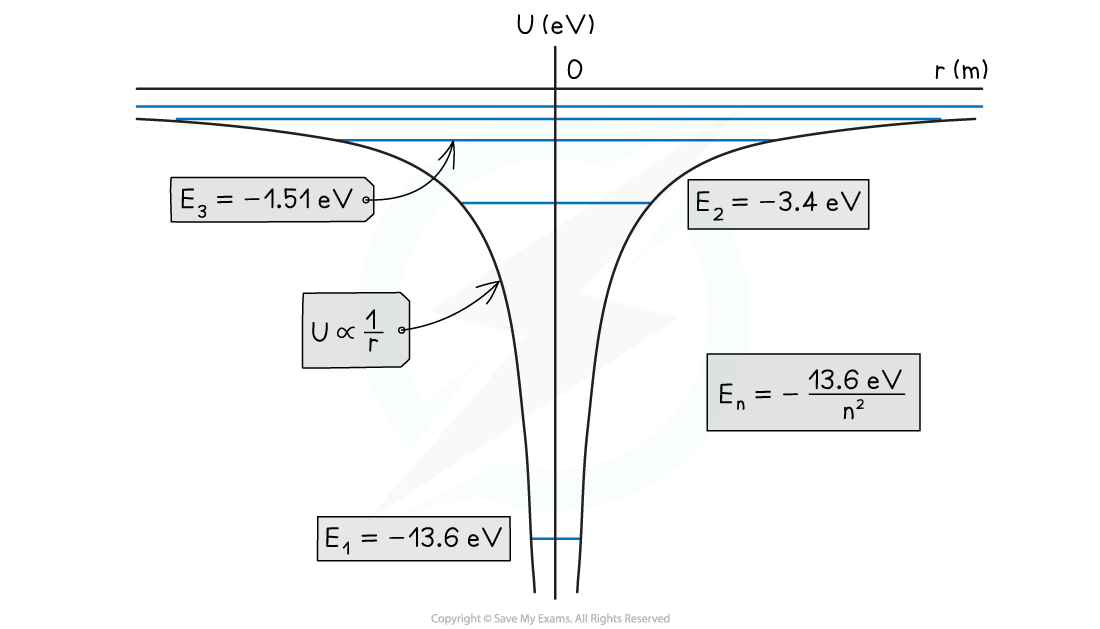
The potential energy curve for hydrogen and the quantised energy levels for n = 1, 2, 3, etc
- On the potential energy curve for hydrogen:
- The higher the energy levels, the closer together they become in energy
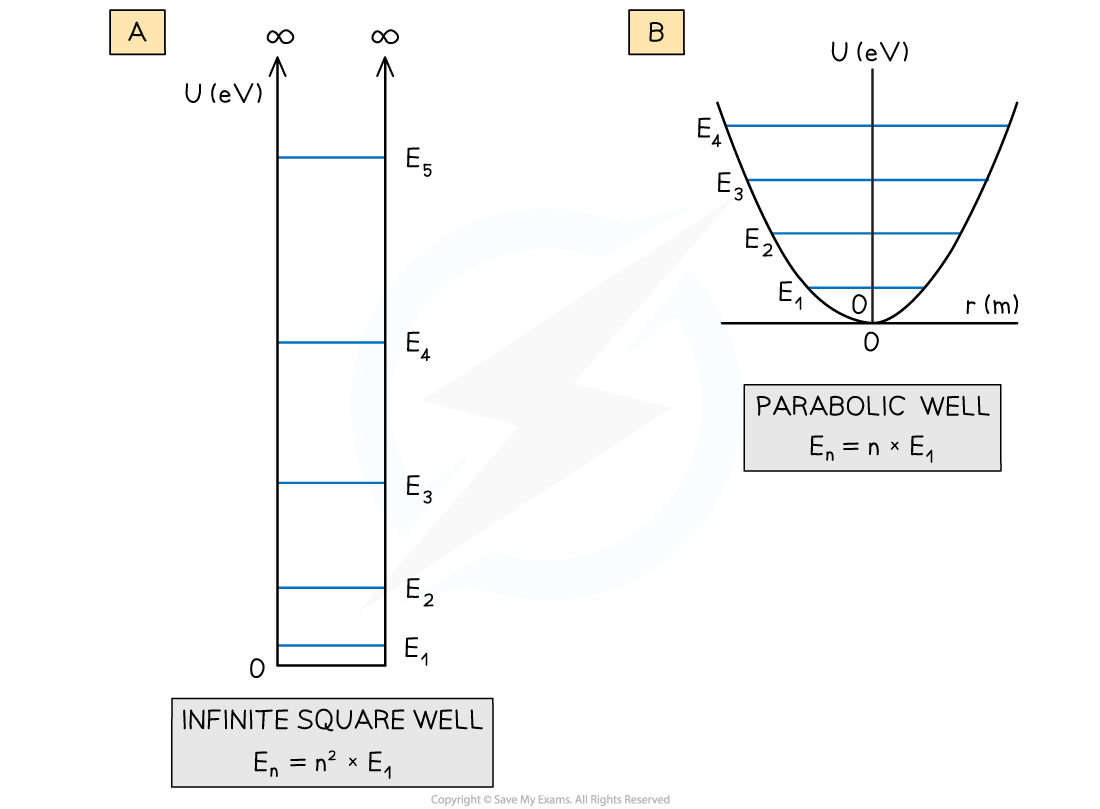
The potential energy curves for (a) an infinite square well and (b) a parabolic well and their associated quantised energy levels
- The shapes of these graphs also produce quantised energy levels but with a different energy distribution
- For the parabolic well, the energy levels are equally spaced
- For the infinite square well, the energy levels at larger energies are further apart – this is different to the case for hydrogen
- Finally, as the infinite square well gets wider, the quantised energy levels get closer together

The "swimming pool" square well where the width is very large. For a wide well, the quantised levels get so close together that the allowed levels are effectively “continuous”
- The Schrodinger equation predicts not only the distribution of energy levels for a particular potential energy curve
- Each energy level also has a wavefunction, usually given the symbol Ψ (Psi)
- Wavefunctions of the infinite square well are shown below
- They look similar to standing waves on a stretched string
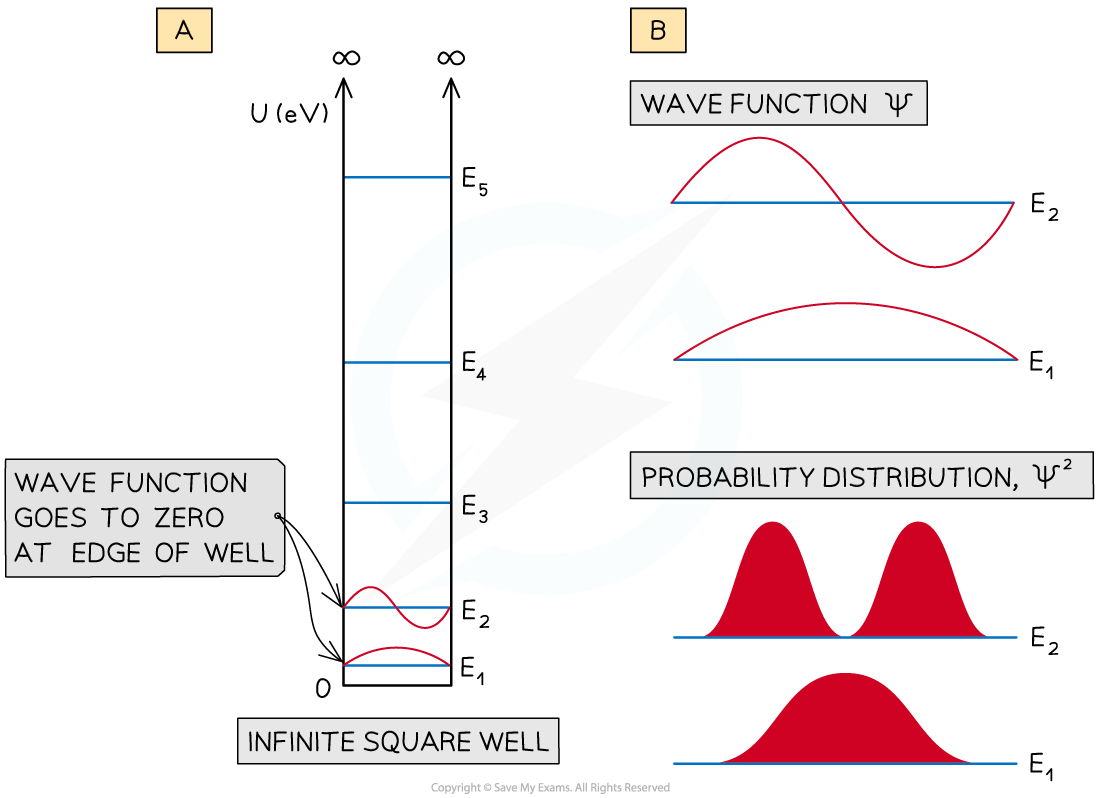
(a) Wave functions for E1 and E2 of an infinite square well. (b) an expanded view of the wavefunctions Ψ, and the probability
- The physical significance of the wavefunction Ψ is that:
- The square of the wavefunction, Ψ2 dr gives the probability of finding the particle in the region of width dr
- The wavefunction is said to be normalised
- This means the probability of finding a particle somewhere in the well at a particular energy level is equal to one
- The infinite square well shows the wave function going to zero at the edges of the well
- This means that the probability of finding the particle close to the walls of the well is small
- For the energy level E1 the probability of finding it at the centre of the well in large
- However, for E2 the probability of finding it at the centre of the well is small
- A different result occurs for a square well that is not infinitely deep
- For two energy levels in a square well, the wave functions penetrate the barrier regions as decaying exponential curves

(a) Wave functions for E1 and E2 for a finite square well. (b) the wavefunctions Ψ, and the probability distribution Ψ^2 are seen to penetrate the barrier
- This means that the probability of finding the particle in the classically forbidden barrier region is not zero





