- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: HL复习笔记12.1.7 Quantization of Angular Momentum
Quantization of Angular Momentum
- Angular momentum is a property of any spinning or rotating body, very similar to linear momentum
- In linear motion, momentum is the product of mass and velocity
- In rotational motion the momentum is the product of moment of inertia and angular speed
- Angular momentum is a vector, this means:
- The magnitude is equal to the momentum of the particle times its radial distance from the centre of its circular orbit
- The direction of the angular momentum vector is normal to the plane of its orbit with the direction being given by the corkscrew rule
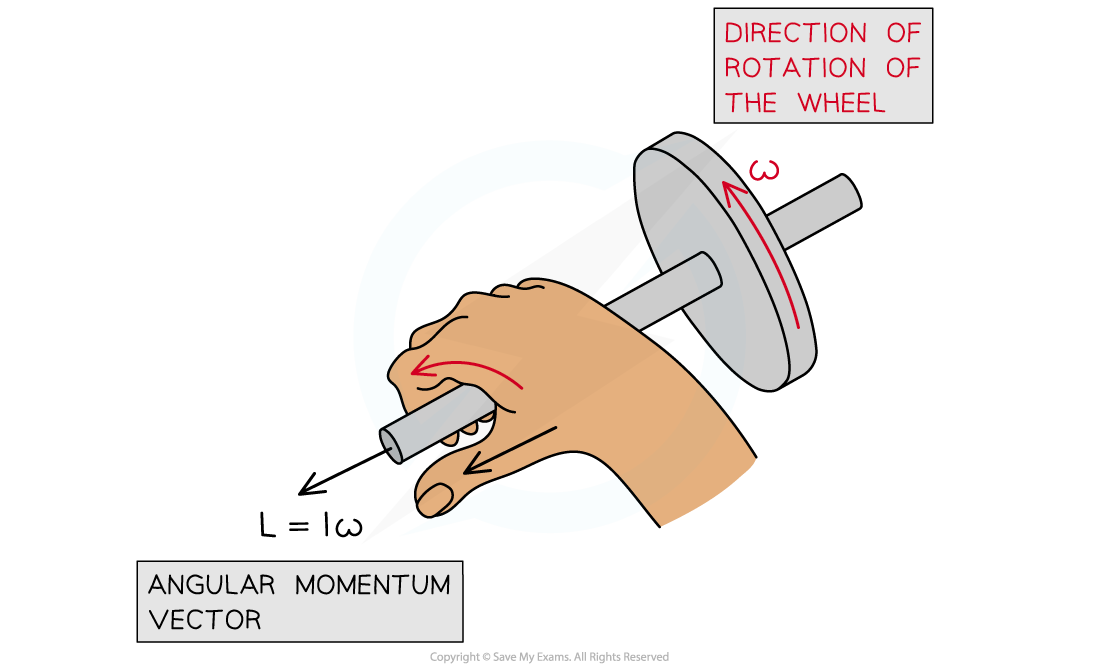
Angular momentum acts at right angles to the direction of rotation
 For an electron moving in a straight line, the matter wave takes a familiar wave shape consisting of peaks and troughs
For an electron moving in a straight line, the matter wave takes a familiar wave shape consisting of peaks and troughs
- Although the electron itself isn't oscillating up and down, only the matter wave

de Broglie matter wave for an electron moving in a straight line at constant speed
- For the same electron moving in a circle, the matter wave still has a sinusoidal shape but is wrapped into a circle

de Broglie matter wave for an electron moving in a circular orbit at constant speed
- As the electron continues to orbit in a circle two possibilities may occur:
1. On completing one oscillation, the waves overlap in phase
-
- The waves will continue in phase over many orbits giving rise to constructive interference and a standing wave

de Broglie matter wave where 3λ is less than the orbits circumference
-
- In other words, peak overlaps with peak, trough with trough
- This means that where the waves overlap, destructive interference occurs and as a result, no such electron orbit is allowed
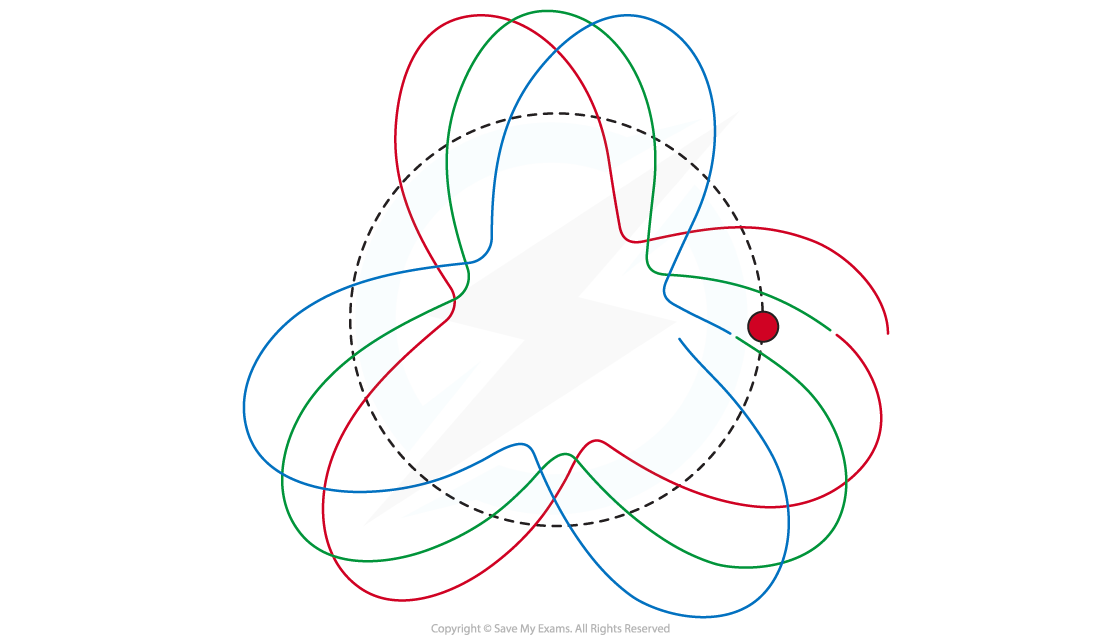
de Broglie matter wave where n = 3. Here the circumference of the circular orbit is 3λ
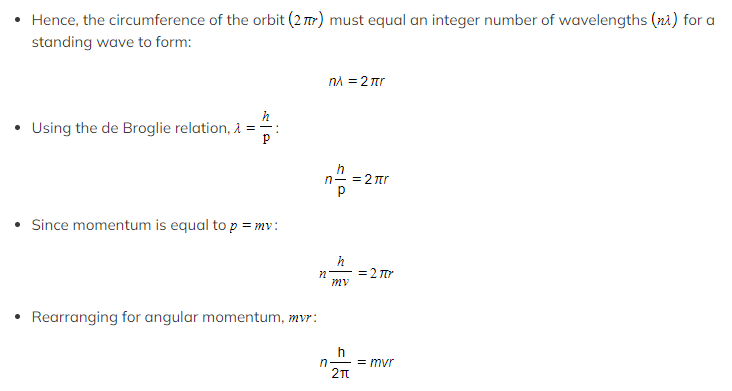 Bohr Condition
Bohr Condition
- The Bohr Condition is given by the relation:

Worked Example
Determine the velocity of the electron in the first Bohr orbit of the hydrogen atom (n = 1).
You may use the following values:
- Mass of an electron = 9.1 × 10−31 kg
- Radius of the orbit = 0.529 × 10−10 m
- Planck's constant = 6.63 × 10−34 kg m2 s-1
Step 1: List the known quantities
-
- Mass of an electron, m = 9.1 × 10−31 kg
- Radius of the orbit, r = 0.529 × 10−10 m
- Planck's constant, h = 6.63 × 10−34 kg m2 s-1
Step 2: Write the Bohr Condition equation and rearrange for velocity, v
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





