- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: HL复习笔记12.1.4 Solving Photoelectric Problems
Solving Photoelectric Problems
- Since energy is always conserved, the energy of an incident photon is equal to:
The work function + the maximum kinetic energy of the photoelectron
- The energy within a photon is equal to hf
- The fraction of the energy transferred to the electron to release it from a material is called the work function, and the remaining amount is given as kinetic energy to the emitted photoelectron
- This equation is known as the photoelectric equation:
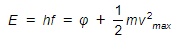 Where:
Where:
- h = Planck's constant (J s)
- f = the frequency of the incident radiation (Hz)
- Φ = the work function of the material (J)
- ½ mv2max = Ek(max) = the maximum kinetic energy of the photoelectrons (J)
- This equation demonstrates:
- If the incident photons do not have a high enough frequency and energy to overcome the work function (Φ), then no electrons will be emitted
- hf0 = Φ, where f0 = threshold frequency, photoelectric emission only just occurs
- Ek(max) depends only on the frequency of the incident photon, and not the intensity of the radiation
- The majority of photoelectrons will have kinetic energies less than Ek(max)
Graphical Representation of Work Function
- The photoelectric equation can be rearranged into the straight line equation:

- A graph of maximum kinetic energy Ek(max) against frequency f can be obtained
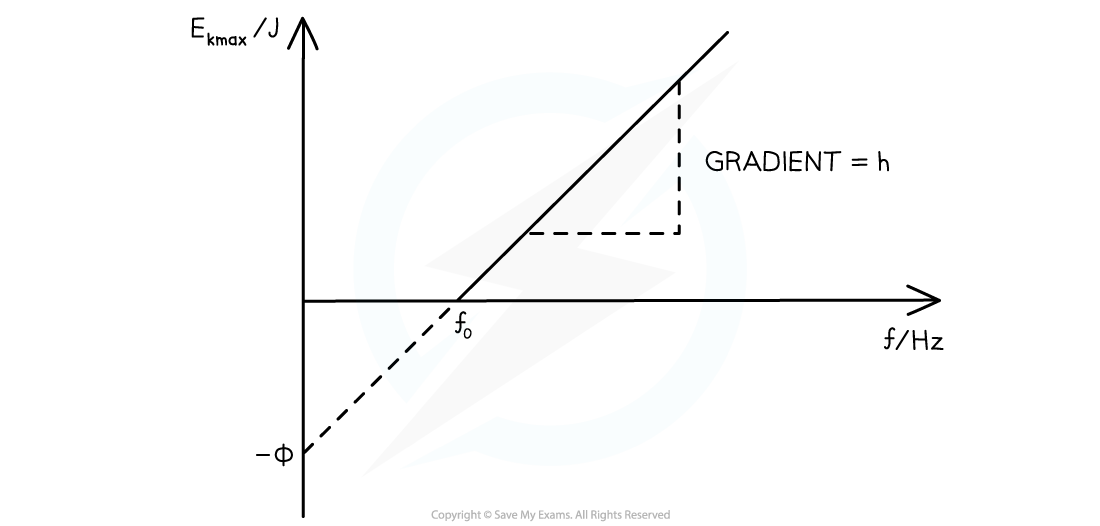
- The key elements of the graph:
- The work function Φ is the y-intercept
- The threshold frequency f0 is the x-intercept
- The gradient is equal to Planck's constant h
- There are no electrons emitted below the threshold frequency f0
Kinetic Energy & Intensity
- The kinetic energy of the photoelectrons is independent of the intensity of the incident radiation
- This is because each electron can only absorb one photon
- Kinetic energy is only dependent on the frequency of the incident radiation
- Intensity is a measure of the number of photons incident on the surface of the metal
- So, increasing the number of electrons striking the metal will not increase the kinetic energy of the electrons, it will increase the number of photoelectrons emitted
Why Kinetic Energy is a Maximum
- Each electron in the metal acquires the same amount of energy from the photons in the incident radiation
- However, the energy required to remove an electron from the metal varies because some electrons are on the surface whilst others are deeper in the metal
- The photoelectrons with the maximum kinetic energy will be those on the surface of the metal since they do not require much energy to leave the metal
- The photoelectrons with lower kinetic energy are those deeper within the metal since some of the energy absorbed from the photon is used to approach the metal surface (and overcome the work function)
- There is less kinetic energy available for these photoelectrons once they have left the metal
Photoelectric Current
- The photoelectric current is the number of photoelectrons emitted per second
- Photoelectric current is proportional to the intensity of the radiation incident on the surface of the metal
- This is because the intensity is proportional to the number of photons striking the metal per second
- Since each photoelectron absorbs a single photon, the photoelectric current must be proportional to the intensity of the incident radiation
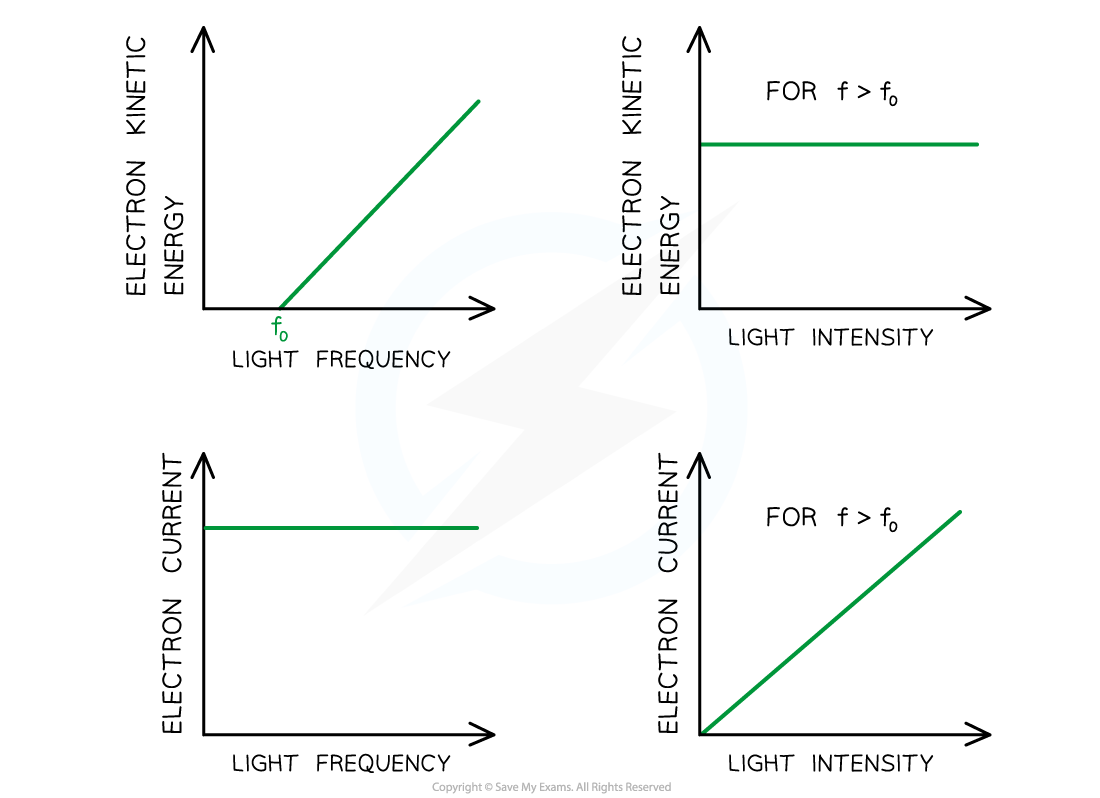
Graphs showing the variation of electron KE and photocurrent with the frequency of the incident light
Worked Example
The graph below shows how the maximum kinetic energy Ek of electrons emitted from the surface of sodium metal varies with the frequency f of the incident radiation.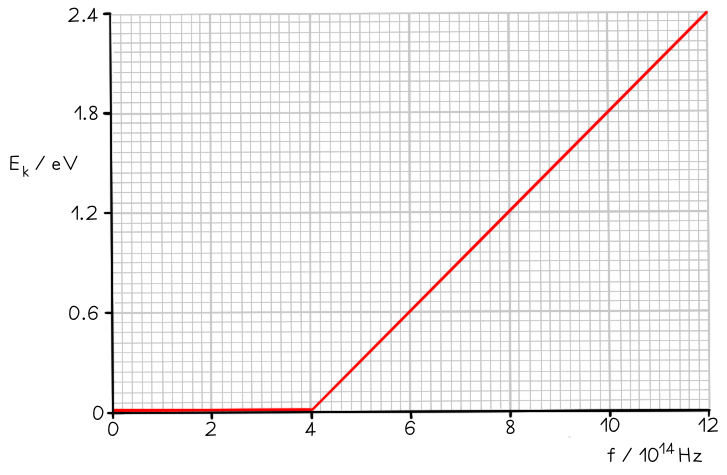
Calculate the work function of sodium in eV.
Step 1: Write out the photoelectric equation and rearrange it to fit the equation of a straight line Exam Tip
Exam Tip
When using the photoelectric effect equation, hf, Φ and Ek(max) must all have the same units; Joules.
All values given in eV need to be converted into Joules by multiplying by 1.6 × 10−19. Do this right away, in the same way as you would convert into SI units before calculating.
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





