- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: HL复习笔记12.1.1 Photons
Photons
- In classical wave theory, electromagnetic (EM) radiation is assumed to behave as a wave
- This is demonstrated by the fact EM radiation exhibits phenomena such as diffraction and interference
- However, experiments from the last century, such as discovering the photoelectric effect and atomic line spectra, can only be explained if the EM radiation is thought of as behaving as particles
- These experiments have formed the basis of quantum theory, which will be explored in detail in this section
Photons
- Photons are fundamental particles which make up all forms of electromagnetic radiation
- A photon is defined as
A massless ''packet'' or a ''quantum'' of electromagnetic energy

A wave packet (photon)
- This means is that the energy of a photon is not transferred continuously, but as discrete packets of energy
- In other words, each photon carries a specific amount of energy, and transfers this energy all in one go, rather than supplying a consistent amount of energy
- The energy of a photon can be calculated using the formula:
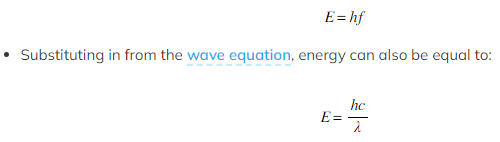 Where:
Where:
-
- E = energy of the photon (J)
- h = Planck's constant (J s)
- c = the speed of light (m s-1)
- f = frequency in Hertz (Hz)
- λ = wavelength (m)
- This equation tells us:
- The higher the frequency of EM radiation, the higher the energy of the photon
- The energy of a photon is inversely proportional to the wavelength
- A long-wavelength photon of light has a lower energy than a shorter-wavelength photon
Worked Example
Light of wavelength 490 nm is incident normally on a surface, as shown in the diagram.
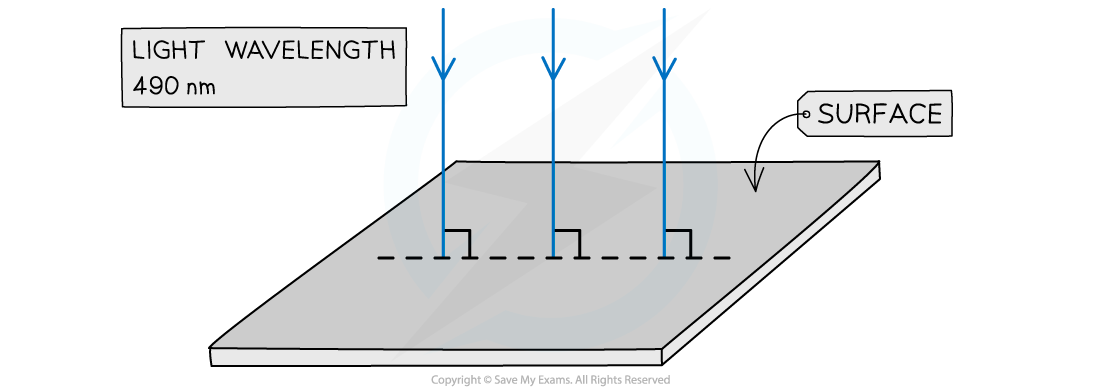
The power of the light is 3.6 mW. The light is completely absorbed by the surface.
Calculate the number of photons incident on the surface in 2.0 s.
Step 1: Write down the known quantities
-
- Wavelength, λ = 490 nm = 490 × 10−9 m
- Power, P = 3.6 mW = 3.6 × 10−3 W
- Time, t = 2.0 s
Step 2: Write the equations for wave speed and photon energy Photon Momentum
Photon Momentum
- Einstein showed that a photon travelling in a vacuum has momentum, despite it having no mass
- The momentum (p) of a photon is related to its energy (E) by the equation:
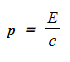
- Where
- c = the speed of light
- p = the momentum of the photon (kg m s-1)
- E = the energy of the photon (J)
Worked Example
Assuming that all the photons are absorbed by the plate, calculate the momentum of the photon, and the pressure exerted by the laser beam on the metal plate.
Step 1: Write down the known quantities
-
- Power, P = 5.0 mW = 5.0 × 10−3 W
- Frequency, f = 5.6 × 1014 Hz
- Cross-sectional area, A = 8.0 × 10−6 m2
Step 2: Write the equations for photon energy and momentum Exam Tip
Exam Tip
The values of Planck’s constant and the speed of light will always be given to you in an exam, however, it helps to memorise them to speed up calculation questions!
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





