- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: HL复习笔记11.3.7 Discharge Calculations
Capacitor Discharge Equation
- The time constant is used in the exponential decay equations for the current, charge or potential difference (p.d) for a capacitor discharging through a resistor
- These can be used to determine the amount of current, charge or p.d left after a certain amount of time for a discharging capacitor
- This exponential decay means that no matter how much charge is initially on the plates, the amount of time it takes for that charge to halve is the same
- The exponential decay of current on a discharging capacitor is defined by the equation:
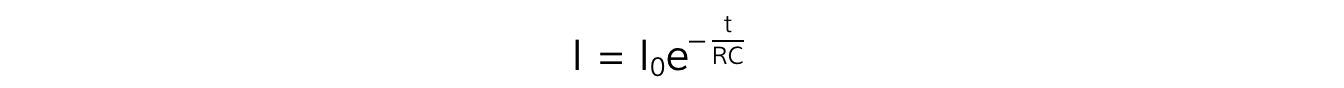
- Where:
- I = current (A)
- I0 = initial current before discharge (A)
- e = the exponential function
- t = time (s)
- RC = resistance (Ω) × capacitance (F) = the time constant τ (s)
- This equation shows that the smaller the time constant τ, the quicker the exponential decay of the current when discharging
- Also, how big the initial current is affects the rate of discharge
- If I0 is large, the capacitor will take longer to discharge
- Note: during capacitor discharge, I0 is always larger than I, as the current I will always be decreasing
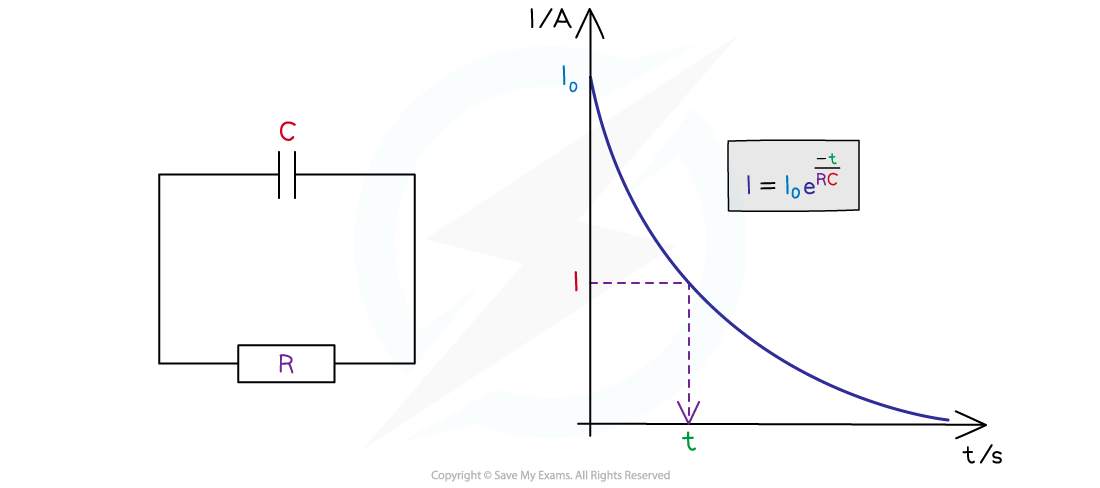
Values of the capacitor discharge equation on a graph and circuit
- The current at any time is directly proportional to the p.d across the capacitor and the charge across the parallel plates
- Therefore, this equation also describes the charge on the capacitor after a certain amount of time:
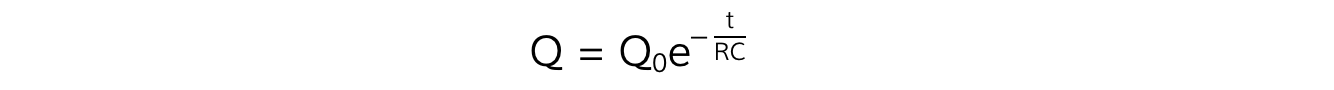
- Where:
- Q = charge on the capacitor plates (C)
- Q0 = initial charge on the capacitor plates (C)
- As well as the p.d after a certain amount of time:
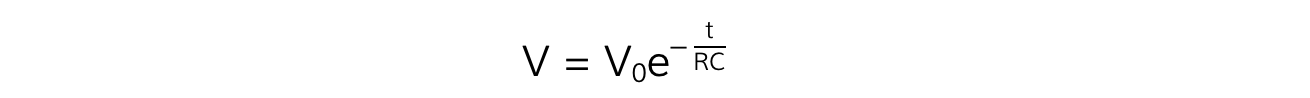
- Where:
- V = p.d across the capacitor (C)
- V0 = initial p.d across the capacitor (C)
The Exponential Function e
- The symbol e represents the exponential constant, a number which is approximately equal to e = 2.718...
- On a calculator, it is shown by the button ex
- The inverse function of ex is ln(y), known as the natural logarithmic function
- This is because, if ex = y, then x = ln (y)
- The 0.37 in the definition of the time constant arises as a result of the exponential constant, the true definition is:
 Worked Example
Worked Example
The initial current through a circuit with a capacitor of 620 µF is 0.6 A. The capacitor is connected across the terminals of a 450 Ω resistor.
Calculate the time taken for the current to fall to 0.4 A.

转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





