- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: HL复习笔记11.2.2 Root-Mean-Square Current & Voltage
Root-Mean-Square Current & Voltage
- Direct current sources provide a constant voltage and current over time, making it easy to measure
- In situations involving alternating voltage and current, the average values of voltage and current will always be zero
- This can make it difficult to measure

The mean value for alternating current and voltage is always zero
- The use of root mean square values gets around this problem
- First remove all the negative signs by simply squaring the peak current, or voltage
- Find the average of the squared value
- And finally, take the square root
- Root-mean-square (rms) values of current, or voltage, are a useful way of comparing a.c current, or voltage, to its equivalent direct current (d.c), or voltage
- The rms values represent the direct current, or voltage, values that will produce the same heating effect, or power dissipation, as the alternating current, or voltage
- The rms value of an alternating current is defined as:
The square root of the mean of squares of all the values of the current in one cycle
- An alternate definition is:
The equivalent direct current that produces the same power
 A resistive load is any electrical component with resistance eg. a lamp
A resistive load is any electrical component with resistance eg. a lamp
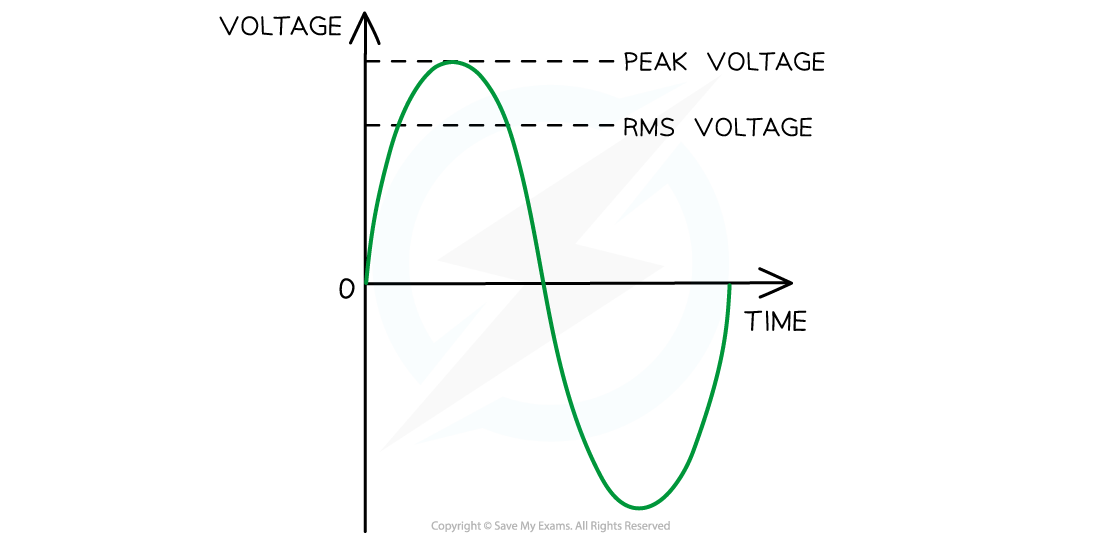
Vrms and peak voltage. The rms voltage is about 70% of the peak voltage
Worked Example
An electric oven is connected to a 230 V root mean square (rms) mains supply using a cable of negligible resistance.
Calculate the peak-to-peak voltage of the mains supply.
Step 1: Write down the Vrms equation 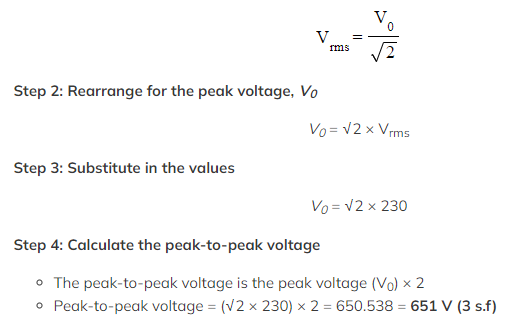
Exam Tip
Remember to double-check the units on the alternating current and voltage graphs. These are often shown in milliseconds (ms) instead of seconds (s) on the x-axis.
Average Power Calculations
- The average power of a supply is the product of the rms current and voltage:
Average power = Irms × Vrms
Worked Example
What is the maximum current supplied to a 2300 W kettle which is connected to an a.c. supply of peak voltage 325 V?

转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





