- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: HL复习笔记11.1.1 Emf, Magnetic Flux & Magnetic Flux Linkage
Emf, Magnetic Flux & Magnetic Flux Linkage
Electromagnetic Induction
- When a conducting wire moves through a magnetic field, a potential difference is created along the wire
- If the wire is part of a closed circuit then an e.m.f is induced
- We can produce a current in a wire simply by moving a magnet near to it
- Electrical energy is produced by the system since work is done on the wire by moving the magnet relative to the free electrons within it
- Therefore, electromagnetic induction is the term applied when an e.m.f. is induced in a closed circuit conductor due to it moving through a magnetic field
- Examples are a flat coil or a solenoid
- Electromagnetic induction happens when a conductor cuts through magnetic field lines
- The amount of e.m.f induced is determined by the magnetic flux and the area on which the magnetic field acts
Magnetic Flux
- Magnetic flux is defined as:
The product of the magnetic flux density and the cross-sectional area perpendicular to the direction of the magnetic flux density
- Magnetic flux when the field and motion are at 90o can be calculated using the simple equation:
-
- Where:
- Φ = magnetic flux (Wb)
- B = magnetic flux density(T)
- A = cross-sectional area (m2)
- Where:
Changing Angle
- The flux is the total magnetic field that passes through a given area
- It is a maximum when the magnetic field lines are perpendicular to the plane of the area
- It is zero when the magnetic field lines are parallel to the plane of the area
- For a coil, the amount of magnetic flux varies as the coil rotates within the field
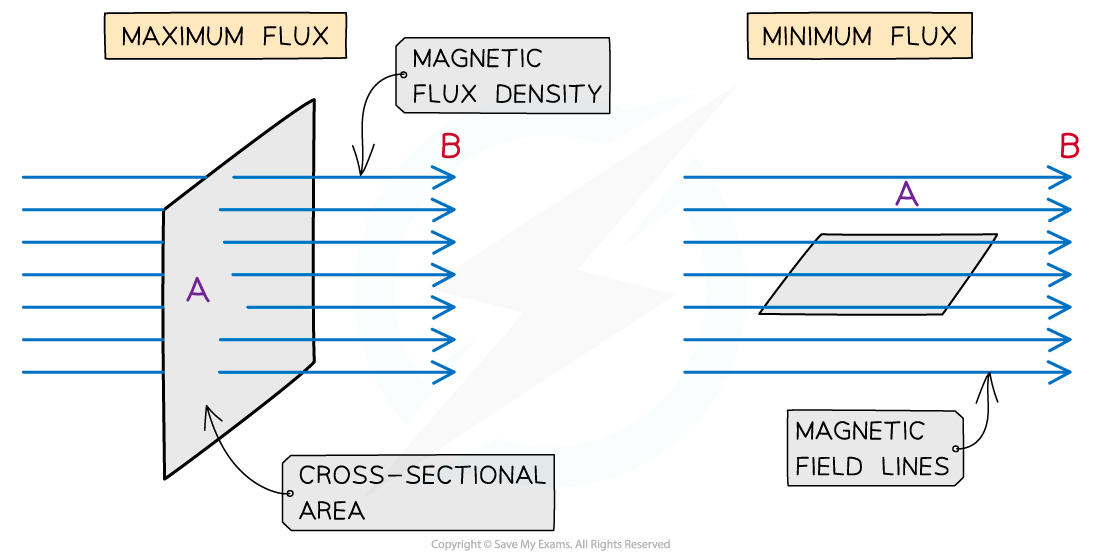
- In other words, magnetic flux is the number of magnetic field lines through a given area
- When the magnetic field lines are not completely perpendicular to the area A, then the component of magnetic flux density B is perpendicular to the area is taken
- The equation then becomes:
Φ = BA cos(θ)
- Where:
- Φ = magnetic flux (Wb)
- B = magnetic flux density (T)
- A = cross-sectional area (m2)
- θ = angle between magnetic field lines and the line perpendicular to the plane of the area (often called the normal line) (degrees)
- This means the magnetic flux is:
- Maximum = BA when cos(θ) =1 therefore θ = 0o. The magnetic field lines are perpendicular to the plane of the area
- Minimum = 0 when cos(θ) = 0 therefore θ = 90o. The magnetic fields lines are parallel to the plane of the area
Worked Example
An aluminium window frame has width of 40 cm and length of 73 cm.
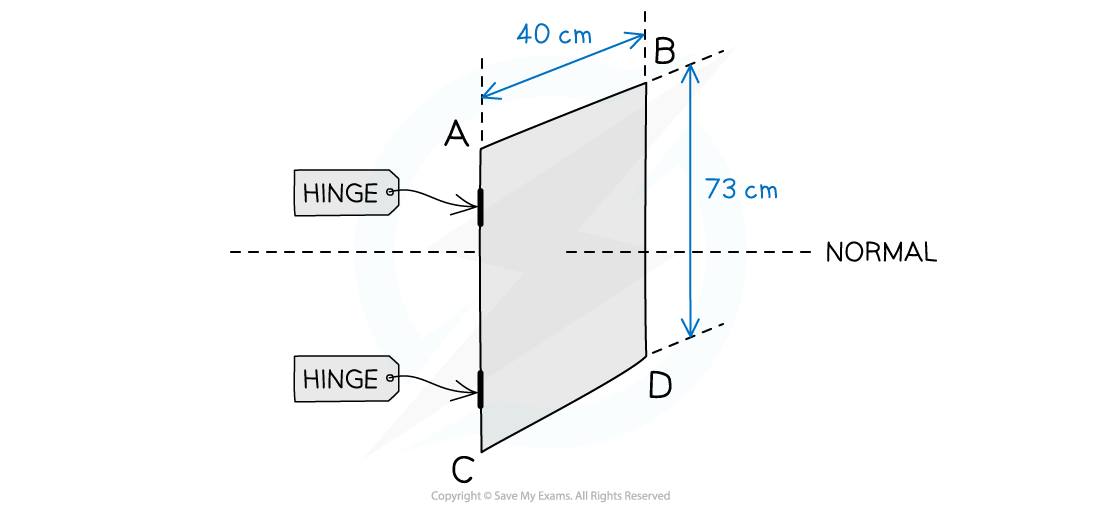
The frame is hinged along the vertical edge AC. When the window is closed, the frame is normal to the Earth's magnetic field with magnetic flux density 1.8 × 10-5 T.
a) Calculate the magnetic flux through the window when it is closed.
b) Sketch the graph of the magnetic flux against angle between the field lines and the normal when the window is opened and rotated by 180°
Part (a)
-
- Cross-sectional area, A = 40 cm × 73 cm = (40 × 10-2) × (73 × 10−2) = 0.292 m2
- Magnetic flux density, B = 1.8 × 10−5 T
Φ = BA
Step 3: Substitute in values
Φ = (1.8 × 10−5) × 0.292 = 5.256 × 10−6 = 5.3 × 10−6 Wb
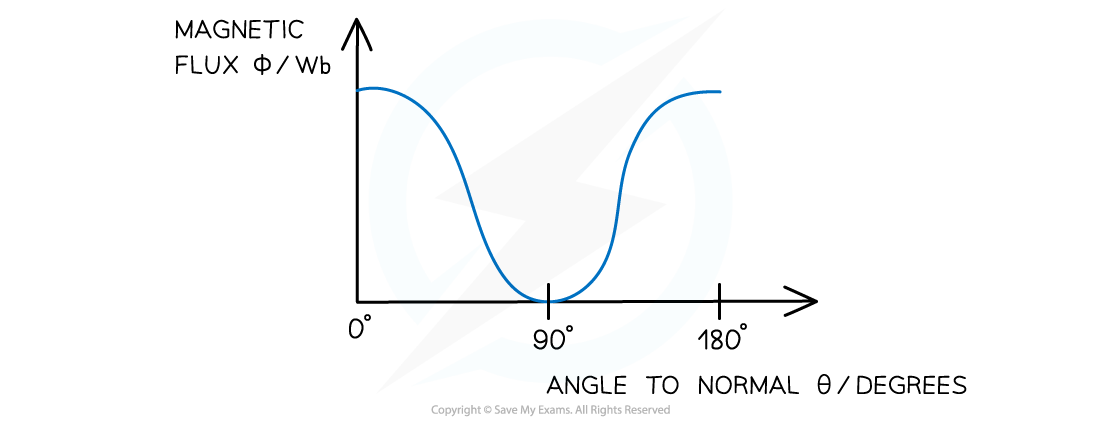
Part (b)
- The magnetic flux will be at a minimum when the window is opened by 90° and a maximum when fully closed or opened to 180°
- This is shown by the graph:
Magnetic Flux Linkage
- More coils in a wire mean a larger e.m.f is induced
- The magnetic flux linkage is a quantity commonly used for solenoids which are made of N turns of wire
- The flux linkage is defined as:
The product of the magnetic flux and the number of turns of the coil
- It is calculated using the equation:
Magnetic flux linkage = ΦN = BAN
-
- Φ = magnetic flux (Wb)
- N = number of turns of the coil
- B = magnetic flux density (T)
- A = cross-sectional area (m2)Where:
- The flux linkage ΦN has the units of Weber turns (Wb turns)
- An e.m.f is induced in a circuit when the magnetic flux linkage changes with respect to time
- This means an e.m.f is induced when there is:
- A changing magnetic flux density B
- A changing cross-sectional area A
- A change in angle θ
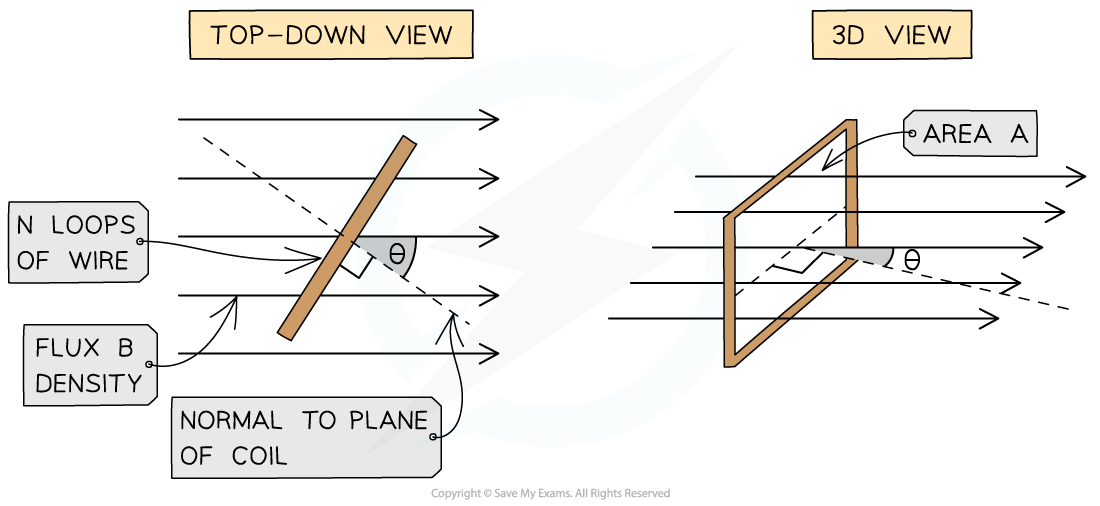
The magnetic flux through a rectangular coil decreases as the angle between the field lines and plane decrease
- Magnetic flux linkage also changes with the rotation of the coil
- It is at a maximum when the field lines are perpendicular to the plane of the area they are passing through
- Therefore, the component of the flux density which is perpendicular is equal to:
ΦN = BAN cos(θ)
- Where:
- N = number of turns of the coil
Exam Tip
The vocabulary in this topic; induced emf, induced current, magnetic flux, magnetic flux density, can be confusing. Until you are absolutely clear which is which, you will struggle to answer questions using the correct equation. Spend some time with your revision notes making sure you are secure with using and understanding the terms.
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





