- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: HL复习笔记10.2.8 Forces on Charges & Masses
Forces on Charges & Masses
- The electric field strength equation can be rearranged for the force F on a charge Q in an electric field E:
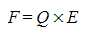 Where:
Where:
- F = electrostatic force on the charge (N)
- Q = charge (C)
- E = electric field strength (N C-1)
- The direction of the force is determined by the charge:
- If the charge is positive (+) the force is in the same direction as the E field
- If the charge is negative (-) the force is in the opposite direction to the E field
- The force on the charge will cause the charged particle to accelerate if its in the same direction as the E field, or decelerate if in the opposite
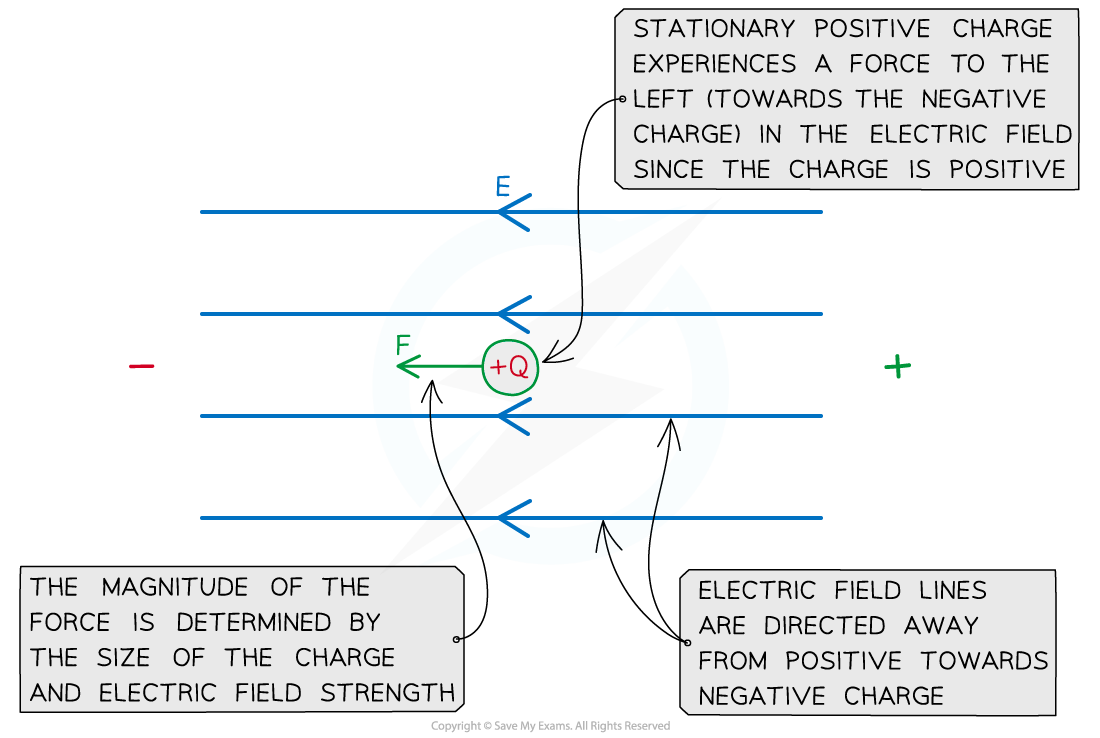
An electric field strength E exerts a force F on a charge +Q in a uniform electric field
- Note: the force will always be parallel to the electric field lines
Motion of Charged Particles
- A charged particle in an electric field will experience a force on it that will cause it to move
- If a charged particle remains still in a uniform electric field, it will move parallel to the electric field lines (along or against the field lines depending on its charge)
- If a charged particle is in motion through a uniform electric field (e.g. between two charged parallel plates), it will experience a constant electric force and travel in a parabolic trajectory
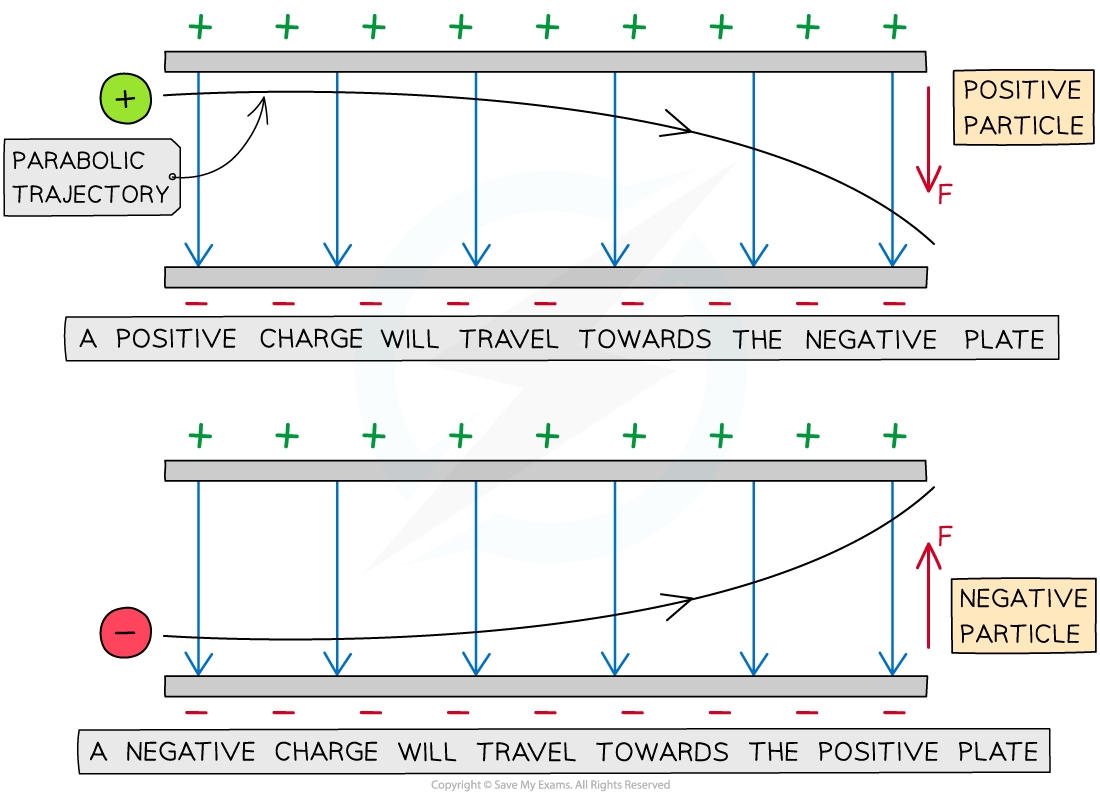
The parabolic path of charged particles in a uniform electric field
- The direction of the parabola will depend on the charge of the particle
- A positive charge will be deflected towards the negative plate
- A negative charge will be deflected towards the positive plate
- The force on the particle is the same at all points and is always in the same direction
- Note: an uncharged particle, such as a neutron experiences no force in an electric field and will therefore travel straight through the plates undeflected
- The amount of deflection depends on the following properties of the particles:
- Mass – the greater the mass, the smaller the deflection and vice versa
- Charge – the greater the magnitude of the charge of the particle, the greater the deflection and vice versa
- Speed – the greater the speed of the particle, the smaller the deflection and vice versa
Worked Example
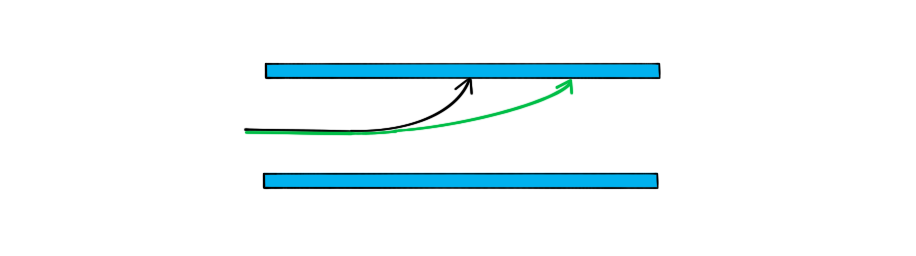
A single proton travelling with a constant horizontal velocity enters a uniform electric field between two parallel charged plates.The diagram shows the path taken by the proton.

Draw the path taken by a boron nucleus that enters the electric field at the same point and with the same velocity as the proton.Atomic number of boron = 5
Mass number of boron = 11
Step 1: Compare the charge of the boron nucleus to the proton
-
- Boron has 5 protons, meaning it has a charge 5 × greater than the proton
- The force on boron will therefore be 5 × greater than on the proton
Step 2: Compare the mass of the boron nucleus to the proton
-
- The boron nucleus has a mass of 11 nucleons meaning its mass is 11 × greater than the proton
- The boron nucleus will therefore be less deflected than the proton
Step 3: Draw the trajectory of the boron nucleus
-
- Since the mass comparison is much greater than the charge comparison, the boron nucleus will be much less deflected than the proton
- The nucleus is positively charged since the neutrons in the nucleus have no charge
- Therefore, the shape of the path will be the same as the proton
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





