- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: HL复习笔记10.2.7 Forces & Inverse-Square Law Behaviour
Forces & Inverse-Square Law Behaviour
- The gravitational force between two bodies outside a uniform field (for example, between the Earth and the Sun) is defined by Newton’s Law of Gravitation which states that:
The gravitational force between two point masses is proportional to the product of the masses and inversely proportional to the square their separation
- In equation form, this can be written as:
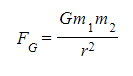 Where:
Where:
- FG = gravitational force between two masses (N)
- G = Newton’s gravitational constant
- m1, m2 = two points masses (kg)
- r = distance between the centre of the two masses (m)
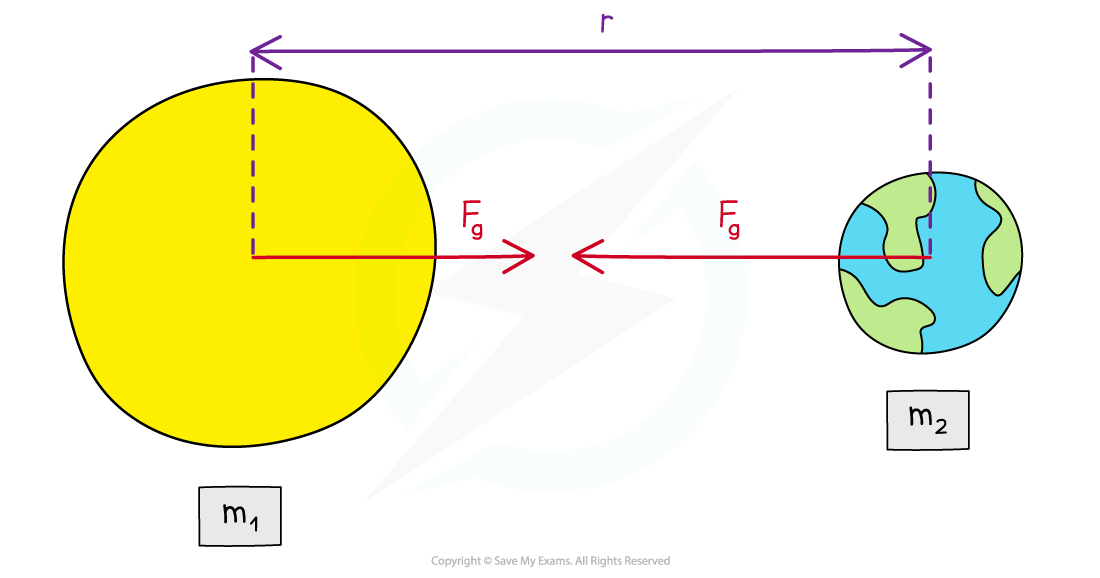
The gravitational force between two masses outside a uniform field is defined by Newton’s Law of Gravitation
- The mass of a uniform sphere can be considered to be a point mass at its centre
- The point mass approximation is a valid assumption if the separation between two objects is much larger than their radii
- This is why Newton’s law of gravitation applies to planets orbiting the Sun
- The 1/r2 relation is called the ‘inverse square law’
- This means that when a mass is twice as far away from another, its force due to gravity reduces by (½)2 = ¼
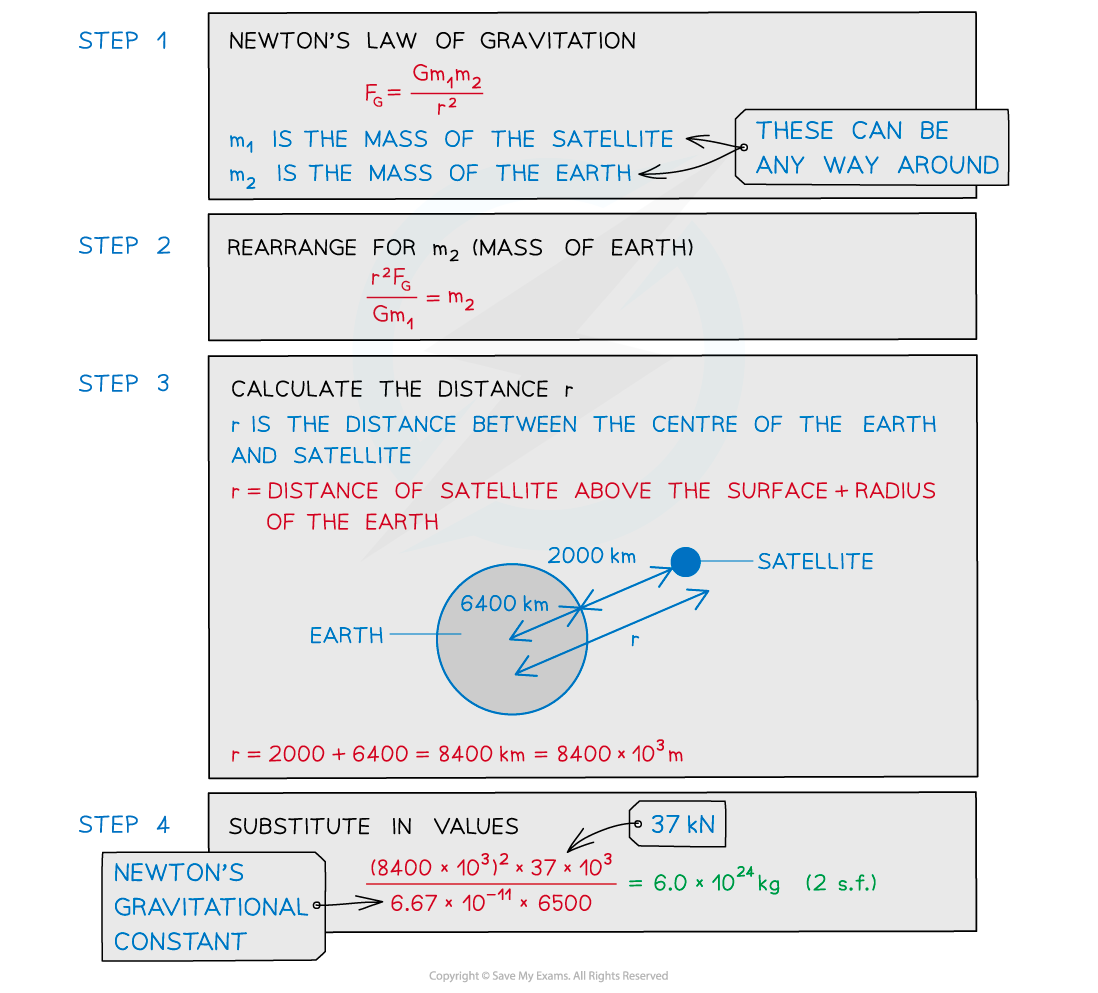
Worked Example
A satellite with a mass of 6500 kg is orbiting the Earth at 2000 km above the Earth's surface. The gravitational force between them is 37 kN.
Calculate the mass of the Earth.
Radius of the Earth = 6400 km.
Coulomb's Law
- All charged particles produce an electric field around it
- This field exerts a force on any other charged particle within range
- The electrostatic force between two charges is defined by Coulomb’s Law
- A charge of a uniform spherical conductor can also be considered as a point charge at its centre
- Coulomb’s Law states that:
The electrostatic force between two point charges is proportional to the product of the charges and inversely proportional to the square of their separation
- The Coulomb equation is defined as:
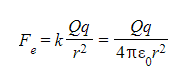
- Where:
- Fe = electrostatic force between two charges (N)
- Q (or Q1) and q (or Q2) = two point charges (C)
- k = Coulomb's constant (8.99 x 109 N m2 C-2)
- ε0 = permittivity of free space
- r = distance between the centre of the charges (m)

The electrostatic force between two charges is defined by Coulomb’s Law
- The 1/r2 relation is called the inverse square law
- This means that when a charge is twice as far as away from another, the electrostatic force between them reduces by (½)2 = ¼
- If there is a positive and negative charge, then the electrostatic force is negative, this can be interpreted as an attractive force
- If the charges are the same, the electrostatic force is positive, this can be interpreted as a repulsive force
- Since uniformly charged spheres can be considered as point charges, Coulomb’s law can be applied to find the electrostatic force between them as long as the separation is taken from the centre of both spheres
Worked Example
An alpha particle is situated 2.0 mm away from a gold nucleus in a vacuum. Assuming them to be point charges, calculate the magnitude of the electrostatic force acting on each of the charges. Atomic number of helium = 2, Atomic number of gold = 79, Charge of an electron = −1.60 × 10-19 C.
Step 1: Write down the known quantities
-
- Distance, r = 2.0 mm =2.0 × 10-3 m
- The charge of one proton = +1.60 × 10-19 C
- An alpha particle (helium nucleus) has 2 protons
- Charge of alpha particle, Q1 = 2 × 1.60 × 10-19 = +3.2 × 10-19 C
- The gold nucleus has 79 protons
- Charge of gold nucleus, Q2 = 79 × 1.60 × 10-19 = +1.264 × 10-17 C
Step 2: The electrostatic force between two point charges is given by Coulomb’s Law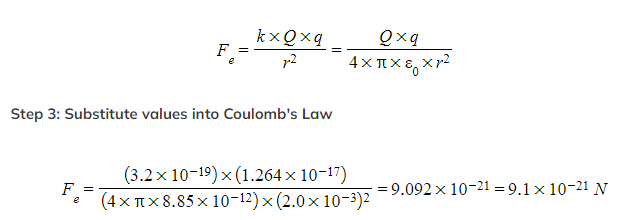 Exam Tip
Exam Tip
A common mistake in exams is to forget to add together the radius of the planet (which is the distance from the centre of mass to the surface) and then, the height above the surface of the planet.
Sketching a diagram will remind you of these two distances and is really a few seconds well spent!
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





