- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: HL复习笔记10.2.5 Escape Speed
Escape Speed
- To escape a gravitational field, a mass must travel at the escape velocity
- This is dependent on the mass and radius of the object creating the gravitational field, such as a planet, a moon or a black hole
- Escape velocity is defined as:
The minimum speed that will allow an object to escape a gravitational field with no further energy input
- It is the same for all masses in the same gravitational field ie. the escape velocity of a rocket is the same as a tennis ball on Earth
- An object reaches escape velocity when all its kinetic energy has been transferred to gravitational potential energy
- This is calculated by equating the equations:
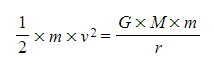 Where:
Where:
- m = mass of the object in the gravitational field (kg)
- v = escape velocity of the object (m s-1)
- G = Newton's Gravitational Constant
- M = mass of the object to be escaped from (ie. a planet) (kg)
- r = distance from the centre of mass M (m)
- Since mass m is the same on both sides of the equations, it can cancel on both sides of the equation:
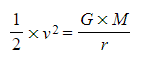
- Multiplying both sides by 2 and taking the square root gives the equation for escape velocity, v:
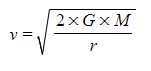
- This equation is not given on the datasheet. Be sure to memorise how to derive it
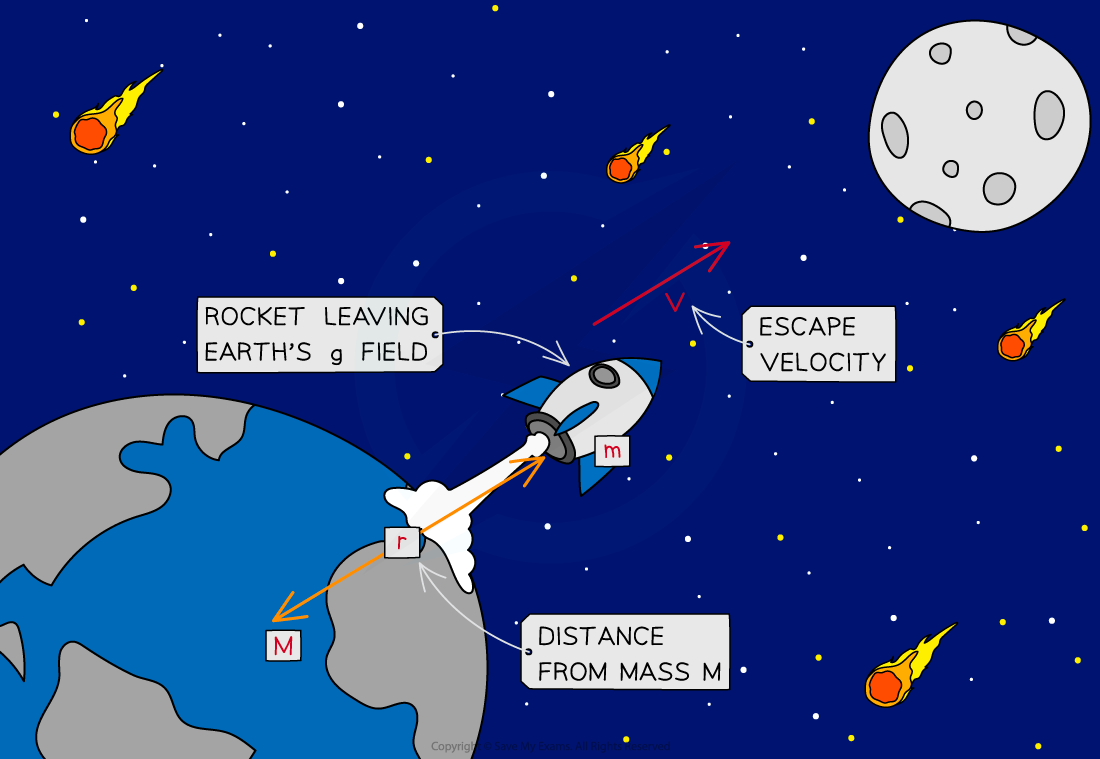
For an object to leave the Earth's gravitational field, it will have to travel at a speed greater than the Earth's escape velocity, v
- Rockets launched from the Earth's surface do not need to achieve escape velocity to reach their orbit around the Earth
- This is because:
- They are continuously given energy through fuel and thrust to help them move
- Less energy is needed to achieve orbit than to escape from Earth's gravitational field
- The escape velocity is not the velocity needed to escape the planet but to escape the planet's gravitational field altogether
- This could be quite a large distance away from the planet
Worked Example
Calculate the escape velocity at the surface of the Moon given that its density is 3340 kg m-3 and has a mass of 7.35 × 1022 kg.Newton's Gravitational Constant = 6.67 × 10-11 N m2 kg-2
 Exam Tip
Exam Tip
When writing the definition of escape velocity, avoid terms such as 'gravity' or the 'gravitational pull / attraction' of the planet. It is best to refer to its gravitational field.
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





