- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: HL复习笔记9.3.4 The Diffraction Grating Equation
The Diffraction Grating Equation
- The angles at which the maxima of intensity (constructive interference) are produced can be deduced by the diffraction grating equation:

- The lines per m (or per mm, per nm etc.) on the grating is usually represented by the symbol N
- Therefore, the spacing between each slit, d, can be calculated from N using the equation:
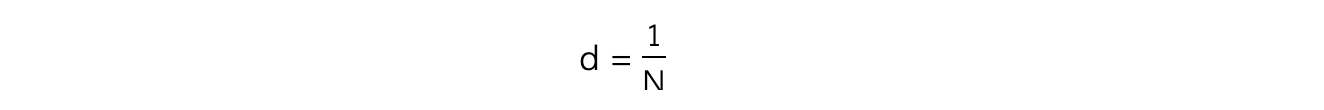
Angular Separation
- The angular separation of each maxima is calculated by rearranging the grating equation to make θ the subject
- The angle θ is taken from the centre meaning the higher orders are at greater angles
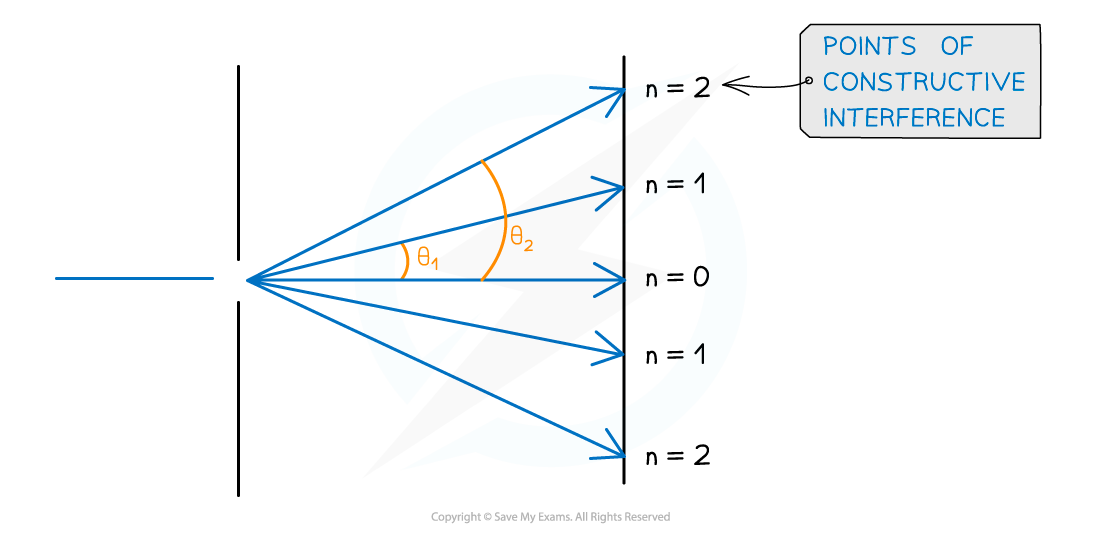
Angular separation
- The angular separation between two angles is found by subtracting the smaller angle from the larger one
- The angular separation between the first and second maxima n1 and n2 is θ2 – θ1
Orders of Maxima
- The maximum angle to see orders of maxima is when the beam is at right angles to the diffraction grating
- This means θ = 90o and sin θ = 1
- The highest order of maxima visible is therefore calculated by the equation:
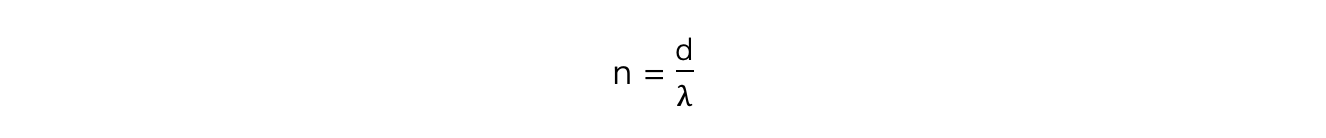
- Note that since n must be an integer, if the value is a decimal it must be rounded down
- E.g If n is calculated as 2.7 then n = 2 is the highest order visible
Worked Example
An experiment was set up to investigate light passing through a diffraction grating with a slit spacing of 1.7 µm. The fringe pattern was observed on a screen. The wavelength of the light is 550 nm.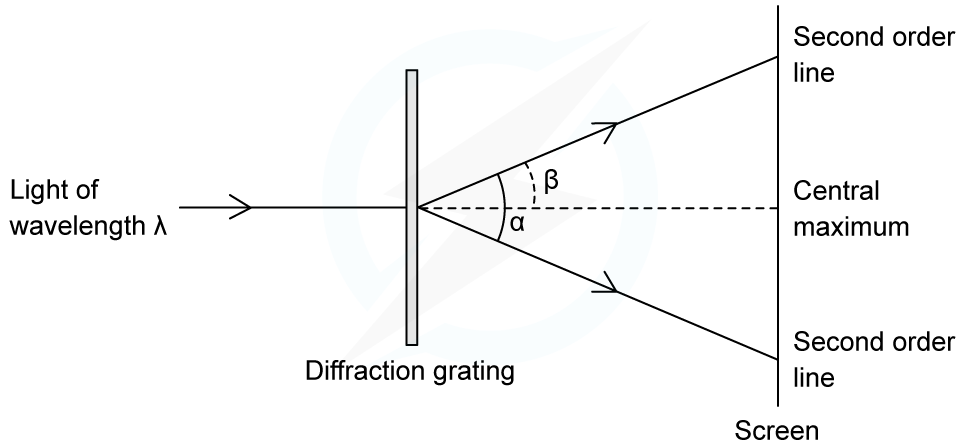
Calculate the angle α between the two second-order lines.

Derivation of the Diffraction Grating Equation
- When light passes through the slits of the diffraction grating, the path difference at the zeroth order maximum is zero
- At the first-order maxima (n = 1), there is constructive interference, hence the path difference is λ
- Therefore, at the nth order maxima, the path difference is equal to nλ
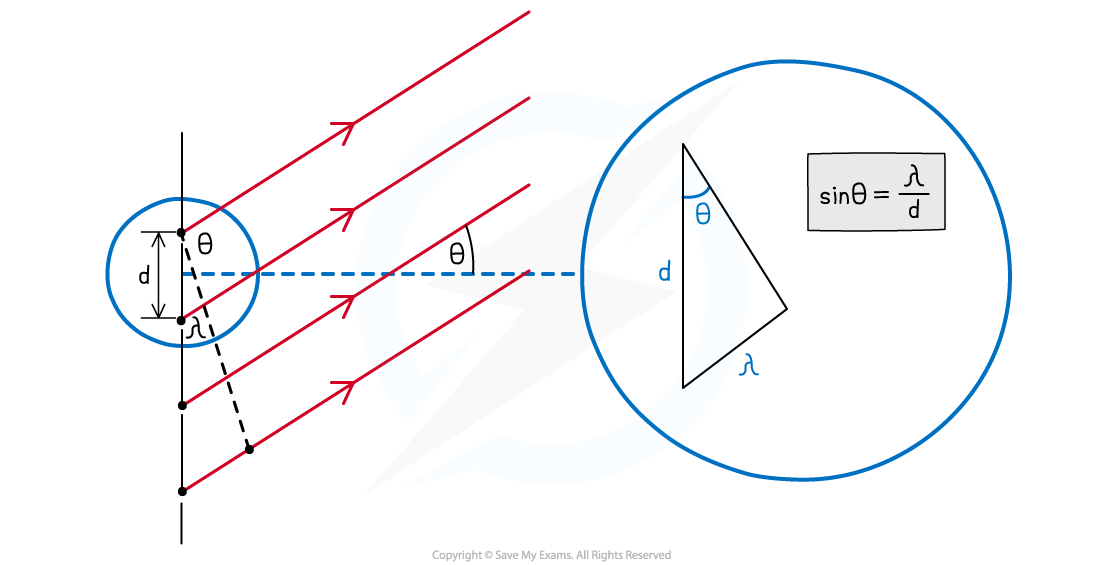
Using this diagram and trigonometry, the diffraction grating equation can be derived
- Using trigonometry, an expression for the first order maxima can be written:
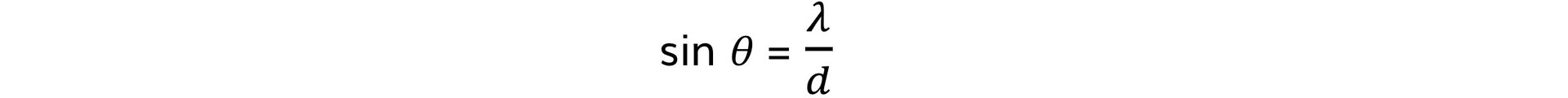
- Where:
- θ = the angle between the normal and the maxima
- λ = the wavelength of the light (m)
- d = the slit separation (m)
- This means, for n = 1:
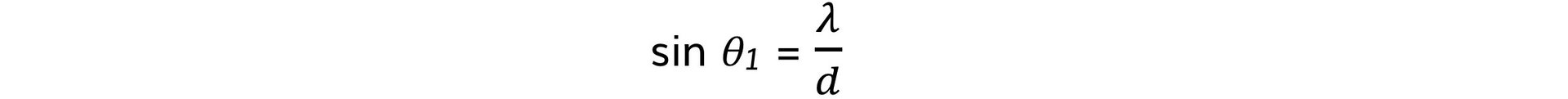
- Similarly, for n = 2, where the path difference is 2λ:
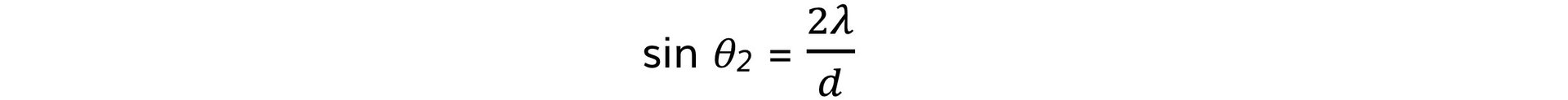
- Therefore, in general, where the path difference is nλ:
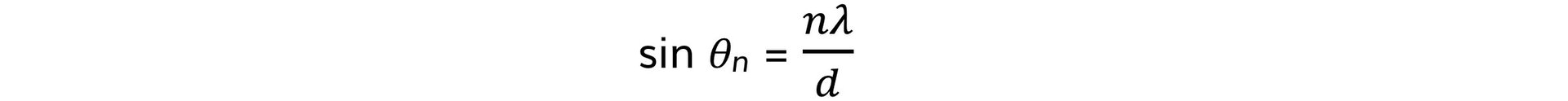
- A small rearrangement leads to the equation for the diffraction grating:
d sin θn = nλ
Exam Tip
Take care that the angle θ is the correct angle taken from the centre and not the angle taken between two orders of maxima.
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





