• Using different sources of monochromatic light demonstrate that:
  • Increasing the wavelength increases the width of the fringes
• The angle of diffraction of the first minima can be found using the equation:

• 
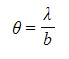
•  Where:
  • θ = the angle of diffraction (radians)
  • λ = wavelength (m)
  • b = slit width (m)

• This equation explains why red light produces wider maxima
  • It is because the longer the wavelength, λ, the larger the angle of diffraction, θ
• It also explains the coloured fringes seen when white light is diffracted
  • It is because red light (longer λ) will diffract more than blue light (shorter λ)
  • This creates fringes which are blue nearer the centre and red further out

• It also explains why wider slits cause the maxima to be narrower
  • It is because the wider the slit, b, the smaller the angle of diffraction, θ

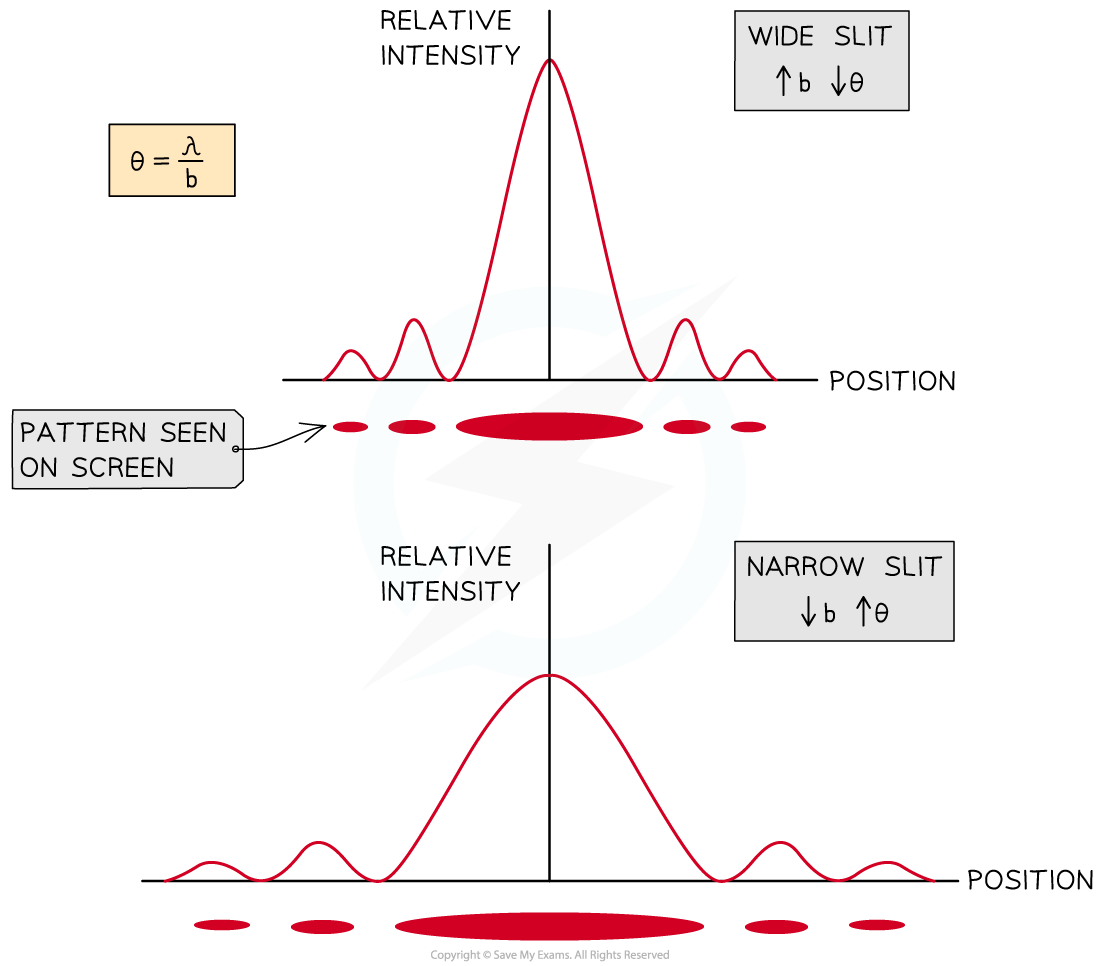
Slit width and angle of diffraction are inversely proportional. Increasing the slit width leads to a decrease in angle of diffraction, hence the maxima appear narrower

Single Slit Geometry

• The diffraction pattern made by waves passing through a slit of width b can be observed on a screen placed a large distance away

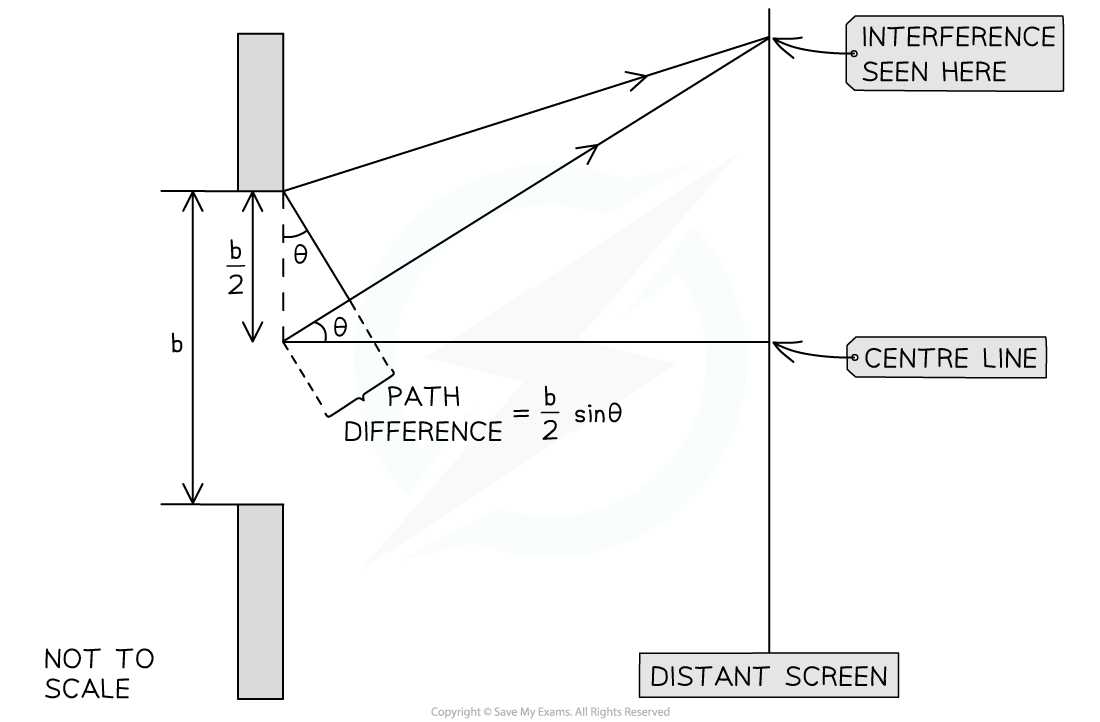
The geometry of single-slit diffraction

Step 1: Write down the equation for the angle of diffraction

Change 3

• • The distance between the slit and the screen will also affect the width of the central fringe
  • A larger distance means the waves must travel further hence, will spread out more
  • Therefore, moving the screen further away would increase the fringe width