- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: HL复习笔记8.2.2 Black-Body Radiation
Black-Body Radiation
- Black body radiation is the name given to the thermal radiation emitted by all bodies (objects)
- All objects, no matter what temperature, emit black body radiation in the form of electromagnetic waves
- These electromagnetic waves usually lie in the infrared region of the spectrum
- Black-body radiation can also be emitted in the form of visible light or other wavelengths, depending on the temperature
- The hotter object, the more infrared radiation it radiates in a given time
- A perfect black body is defined as:
An object that absorbs all of the radiation incident on it and does not reflect or transmit any radiation
- Since a good absorber is also a good emitter, a perfect black body would be the best possible emitter too
- As a result, an object which perfectly absorbs all radiation will be black
- This is because the colour black is what is seen when all colours from the visible light spectrum are absorbed
- The intensity and wavelength distribution of any emitted waves depends on the temperature of the body
- This is represented on a black body radiation curve
- As the temperature increases, the peak of the curve moves
- This moves to a lower wavelength and a higher intensity
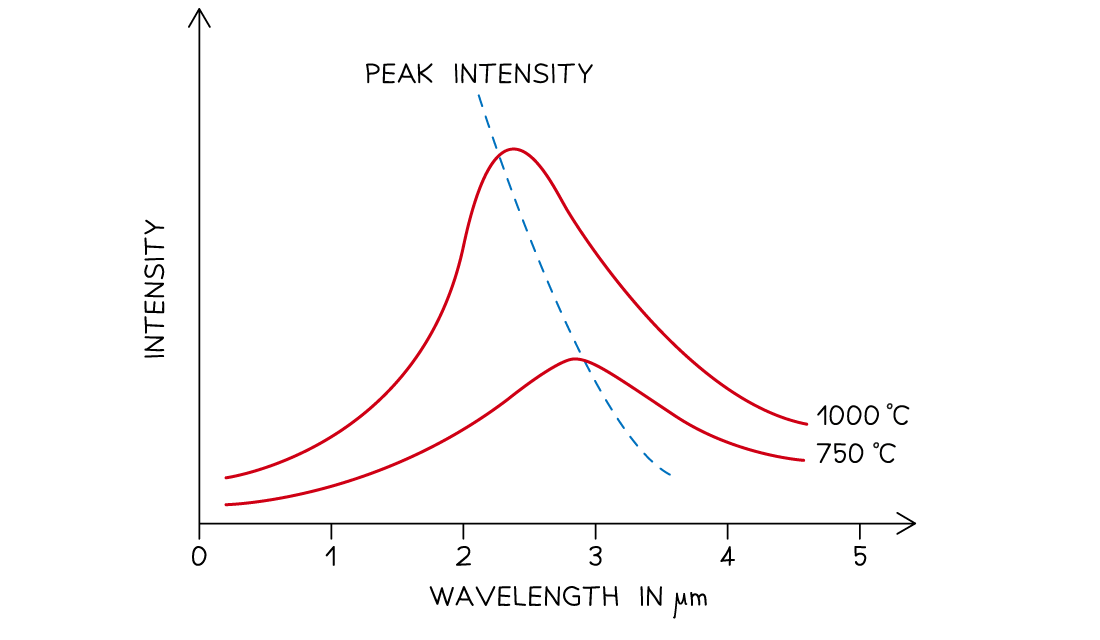
Black body spectrum for objects of different temperatures
- From the electromagnetic spectrum, waves with a smaller wavelength have higher energy (e.g. UV rays, X-rays)
- When an object gets hotter, the amount of thermal radiation it emits increases
- This increases the thermal energy emitted and therefore the wavelength of the emitted radiation decreases
- At room temperature objects emit thermal radiation in the infrared region of the spectrum
- At around 1000 °C an object will emit a significant amount of red light
- At 6000 °C an object will mainly emit white or blue light (and some ultraviolet)
- At even higher temperatures objects will emit ultraviolet or even X-rays
- A black body is an object which:
- Absorbs all the radiation that falls on it, and is also a good emitter
- Does not reflect or transmit any radiation
- A black body is a theoretical object, however, stars are the best approximation there is
- The radiation emitted from a black body has a characteristic spectrum that is determined by the temperature alone
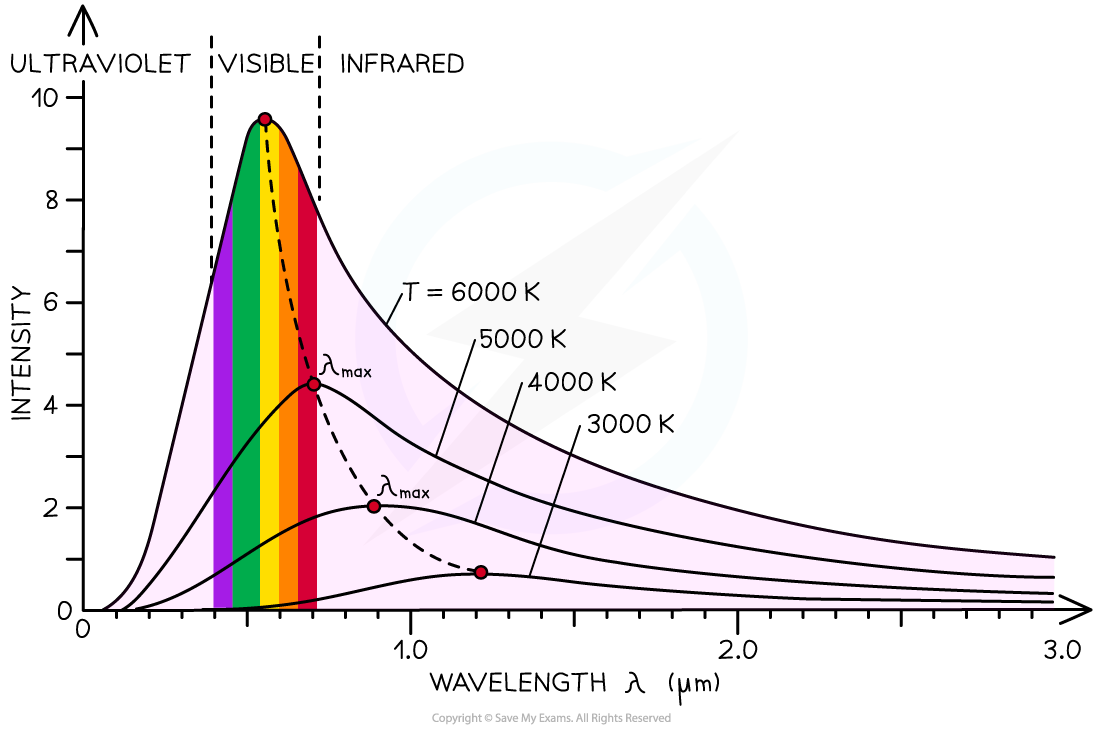
The intensity-wavelength graph shows how thermodynamic temperature links to the peak wavelength for four different bodies
Stefan–Boltzmann Law & Wien’s Displacement Law
Wien’s Displacement Law
- Wien’s displacement law relates the wavelength emitted by a body to its surface temperature, it states:
The black body radiation curve for different temperatures peaks at a wavelength which is inversely proportional to the temperature
- This relation can be written as:
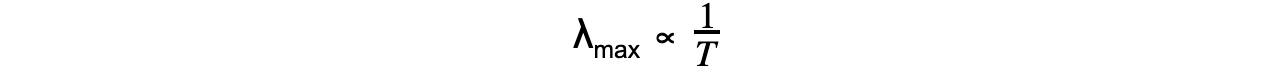
- The full equation for Wien's Law is given by
λmaxT = 2.9 × 10−3 m K
- Where:
- λmax = peak wavelength emitted by the body (m)
- T = temperature of the body (K)
- This equation shows:
- The higher the temperature of a body, the shorter the wavelength it emits at the peak intensity
- The higher the temperature of a body, the greater the intensity of the radiation at each wavelength
Stefan–Boltzmann Law
- The power output of a black body depends on two factors:
- Its surface temperature
- Its radius
- The relationship between these is known as the Stefan-Boltzmann Law, which states:
The total energy emitted by a black body per unit area per second is proportional to the fourth power of the absolute temperature of the body
- It is equal to:
P = σAT4
- Where:
- P = total power emitted by the black body (W)
- σ = the Stefan-Boltzmann constant
- A = total surface area of the black body (m2)
- T = absolute temperature of the body (K)
- When considering a sphere (such as a star) the surface area is equal to 4πr2
- In this case, the Stefan-Boltzmann law can be written as:
P = 4πr2σT4
Worked Example
Betelguese is our nearest red giant star. It has a power output of 4.49 × 1031 W and emits radiation with a peak wavelength of 850 nm.
Calculate the ratio of the radius of Betelgeuse rB to the radius of the Sun rs.
Radius of the sun rs = 6.95 × 108 m.
Step 1: Write down Wien’s displacement law
λmaxT = 2.9 × 10−3 m K
Step 2: Rearrange Wien’s displacement law to find the surface temperature of Betelguese
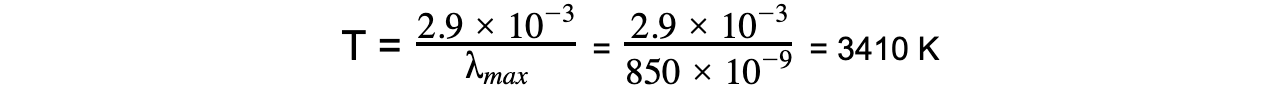
Step 3: Write down the Stefan-Boltzmann law
P = σAT4
P = 4πr2σT4
Step 4: Rearrange for r and calculate the stellar radius of Betelguese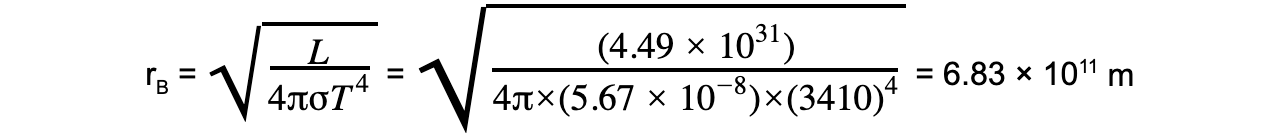
Step 5: Calculate the ratio rB / rs
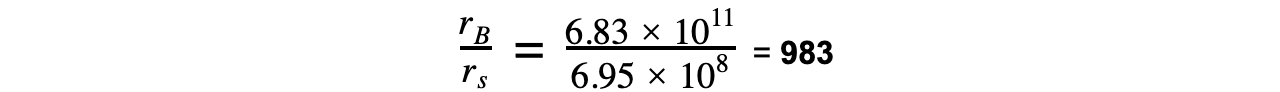
-
- Therefore, the radius of Betelguese is about 1000 times larger than the Sun’s radius
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





