- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: HL复习笔记7.3.4 Particle Conservation Laws
Particle Conservation Laws
Charge
- Electric charge must be conserved during particle interactions
- This means charge must have the same value overall before and after the interaction
- Charge is found in quarks, leptons and exchange particles and their anti-matter counterparts
Baryon Number
- The baryon number, B, is the number of baryons in an interaction
- B depends on whether the particle is a baryon, anti-baryon or neither
- Baryons have a baryon number B = +1
- Anti-baryons have a baryon number B = –1
- Particles that are not baryons have a baryon number B = 0
- Baryon number is a quantum number and is conserved in all interactions
- This is one of the indicators for whether an interaction is able to occur or not
Lepton number
- The lepton number, L, is the number of leptons in an interaction
- L depends on whether the particle is a lepton, anti-lepton or neither
- Leptons have a lepton number L = +1
- Anti-leptons have a lepton number L = –1
- Particles that are not leptons have a lepton number L = 0
- Lepton number is a quantum number and is conserved in all interactions
- This is one of the indicators for whether an interaction is able to occur or not
Conservation Laws
- All particle interactions must obey a set of conservation laws. These are conservation of:
- Charge, Q
- Baryon number, B
- Lepton Number, L
- Strangeness, S
- Energy (or mass-energy)
- Momentum
- However, strangeness does not need to be conserved in weak interactions. It can change by either 0, +1 or –1
- Quantum numbers such as Q, B, L and S can only take discrete values (ie. 0, +1, –1, 1/2)
- To know whether a particle interaction can occur, check whether each quantum number is equal on both sides of the equation
- If even one of them, apart from strangeness in weak interactions, is not conserved then the interaction cannot occur
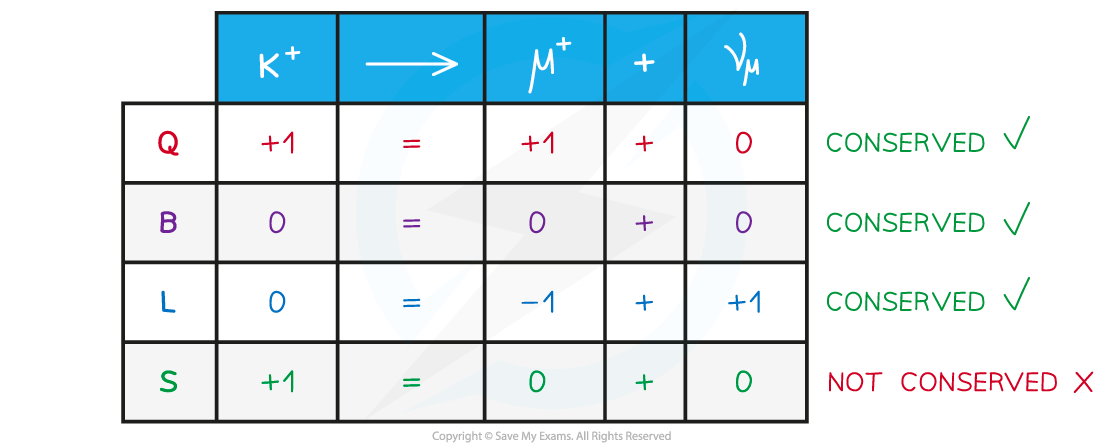
Example of a working out what is conserved in Kaon decay. This decay must be through the weak interaction since S is not conserved
Strangeness
- Strangeness, S, like baryon and lepton number, is a quantum number
- Strangeness is conserved in every interaction except the weak interaction
- This means that strange particles are always produced in pairs (e.g. K+ and K–)
- S depends on whether the particle contains a strange quark, anti-strange quark, or no strange quarks
- Particles with an anti-strange quark have S = +1
- Particle with a strange quark have S = –1
- Particles with no strange quark have S = 0
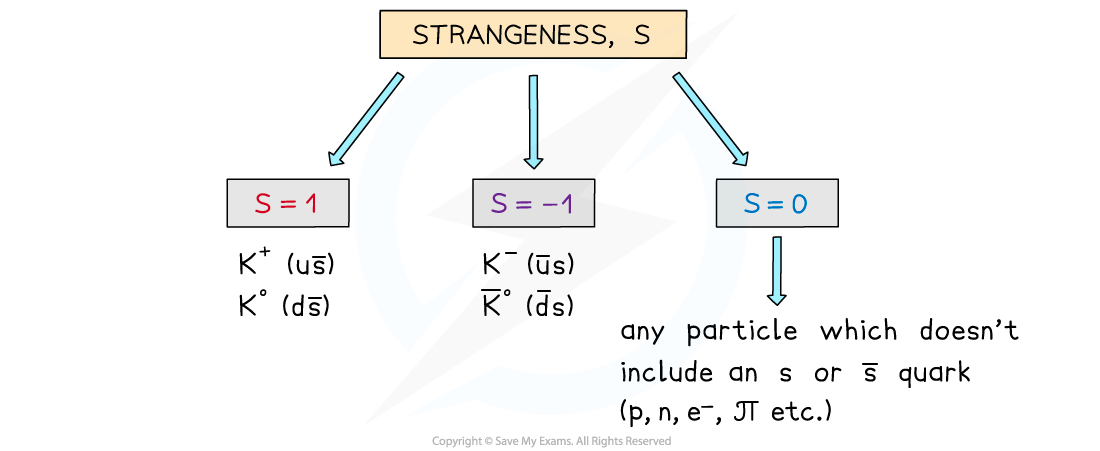
Only particles with a strange or anti-strange quark have a strangeness of +1 or –1
- Strangeness can change by 0, +1 or –1 in weak interactions
Strange Particles
- Strange particles are particles that include a strange or anti-strange quark
- An example of these are kaons
- Strange particles always:
- Are produced through the strong interaction
- Decay through the weak interaction
- An example of a kaon production could be:
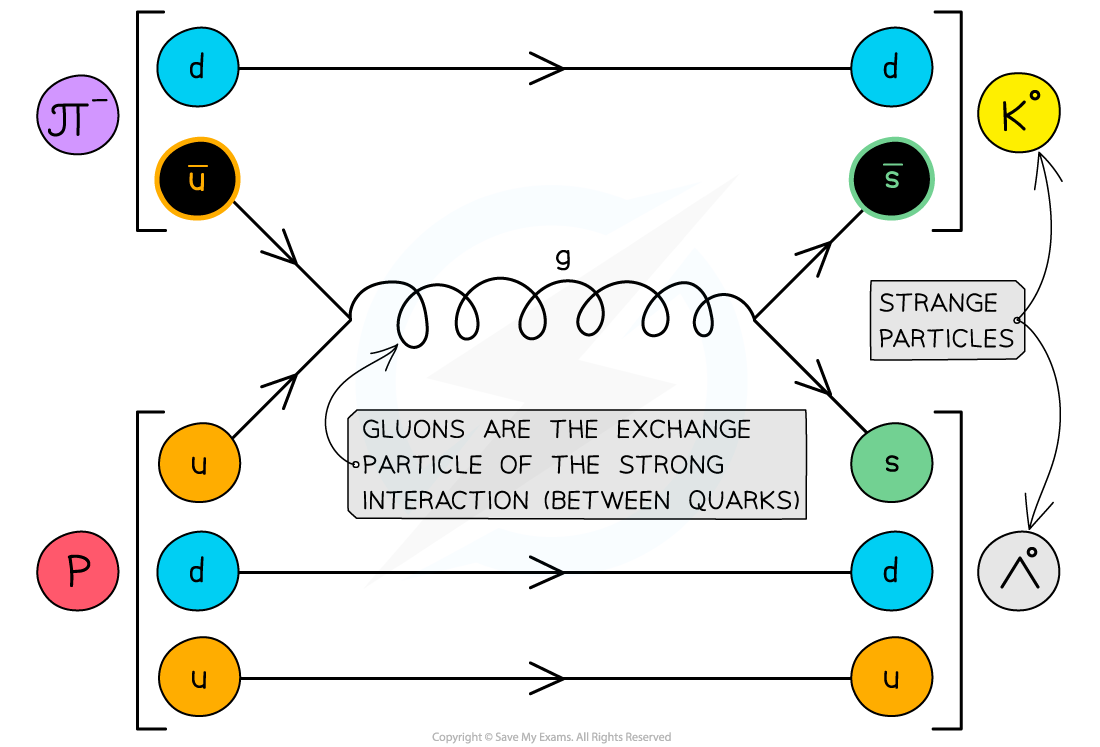
Kaons are produced through the strong interaction. This is shown by the gluon exchange particle.
- An example of kaon decay could be:
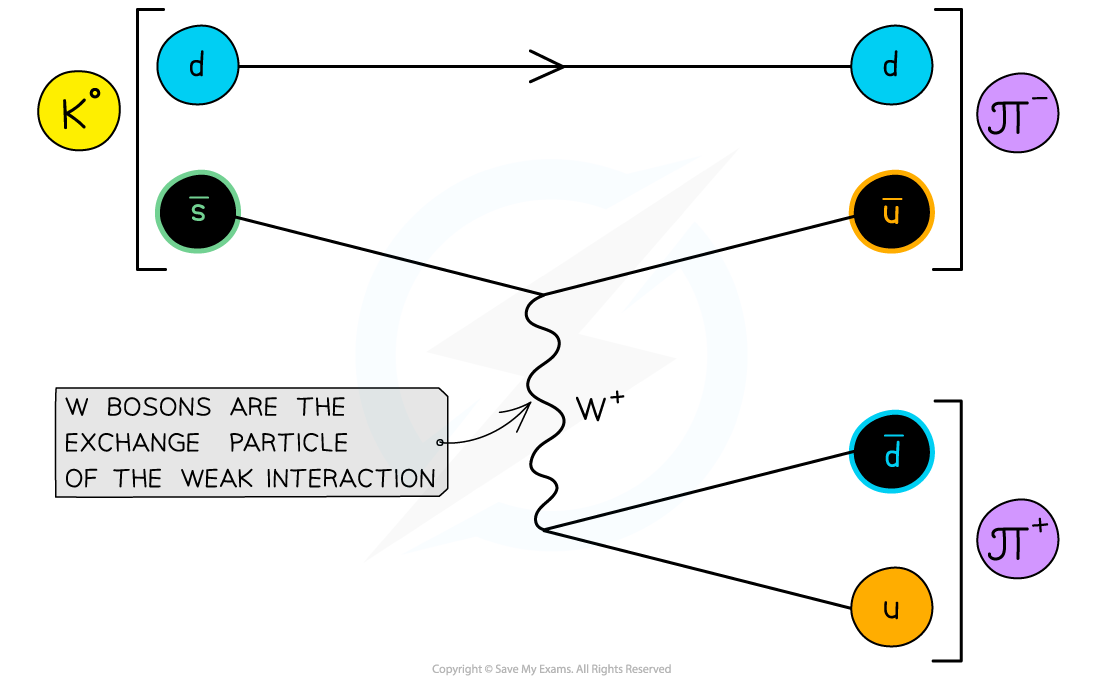
Kaons decay via the weak interaction. This is shown by the W+ boson.
Worked Example
The lambda nought particle Λ0 is has a quark composition uds.
Show, in terms of the conservation of charge, strangeness, baryon number and lepton number whether the following interaction is permitted: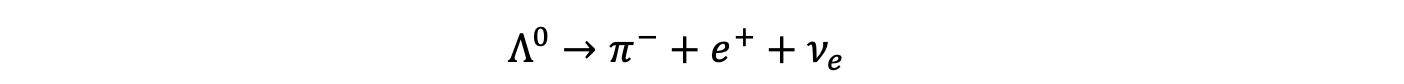
Step 1: Determine conservation of charge, Q
-
- The Λ0 has a charge of 0
- The pion π– has a charge of –1
- The positron e+ has a charge of +1
- The electron neutrino νe has a charge of 0
0 = –1 + 1 + 0
-
- Therefore, charge is conserved
Step 2: Determine conservation of strangeness, S
-
- Λ0 has an s quark, so must have a strangeness of –1
- None of the particles on the right hand side of the decay has a strange quark
–1 = 0 + 0 + 0
-
- Therefore, strangeness is not conserved
Step 3: Determine conservation of baryon number, B
-
- Λ0 is a baryon since it has 3 quarks, so must have a baryon number of +1
- The pion π– is a meson so has a baryon number 0
- The positron is a lepton so has a baryon number 0
- The electron neutrino νe is a lepton so has a baryon number 0
+1 = 0 + 0 + 0
-
- Therefore, baryon number is not conserved
Step 4: Determine conservation of lepton number, L
-
- Λ0 is a baryon, so must have a lepton number of 0
- The pion π– is a meson so has a lepton number of 0
- The positron e+ is an anti-lepton so has a lepton number of –1
- The electron neutrino νe is a lepton so has a lepton number of +1
0 = 0 + (–1) + 1
-
- Therefore, lepton number is conserved
Step 5: Conclusion
-
- Since the baryon number is not conserved, this interaction is not permitted
Worked Example
The equation for β– decay is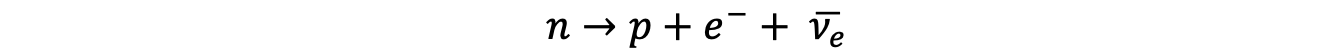
Using the quark model of beta decay, prove that the charge is conserved in this decay.
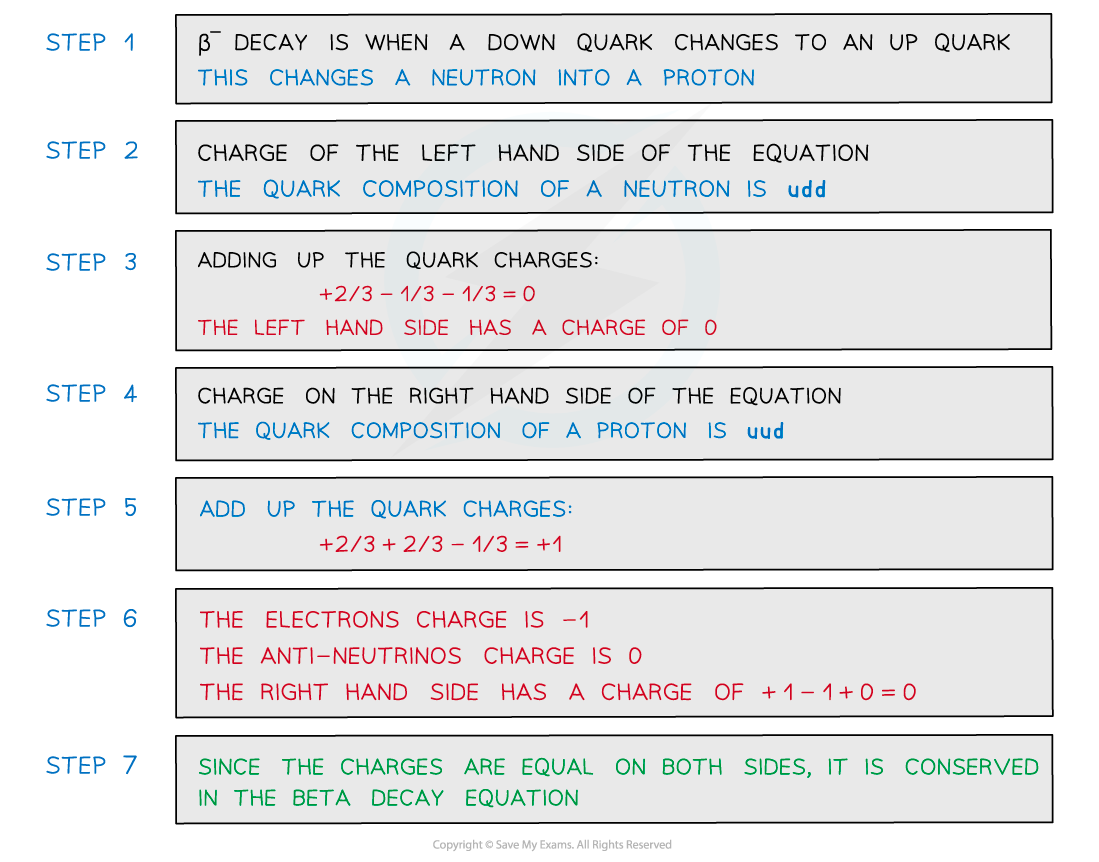
Worked Example
The sigma baryon has a quark structure of suu. It decays to produce a proton and pion as shown in the equation below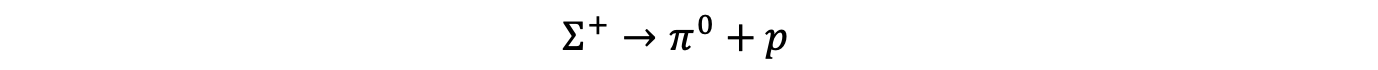 Prove that this decay is via the weak interaction.
Prove that this decay is via the weak interaction.
Step 1: Determine the strangeness, S of each particle
-
- Since sigma baryon has one s quark, it has S = –1
- The proton and pion has no strange particles, so they have S = 0
Step 2: Determine strangeness, S on both sides of the equation
-
- The sigma baryon has a S = –1 but the meson and proton have a S = 0
–1 = 0 + 0
Step 3: Comment on the conservation of strangeness
-
- Since S is not conserved on both sides of the decay equation (only changed by –1), this decay is via the weak interaction
- This is because S is conserved in all other types of interaction (strong and EM), but isn't always conserved in weak interactions
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





