- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: HL复习笔记7.2.2 Mass Defect & Nuclear Binding Energy
Mass Defect & Nuclear Binding Energy
Energy & Mass Equivalence
- Einstein showed in his Theory of Relativity that matter can be considered a form of energy and hence, he proposed:
- Mass can be converted into energy
- Energy can be converted into mass
- This is known as mass-energy equivalence, and can be summarised by the equation:
E = mc2
- Where:
- E = energy (J)
- m = mass (kg)
- c = the speed of light (m s-1)
- Some examples of mass-energy equivalence are:
- The fusion of hydrogen into helium in the centre of the sun
- The fission of uranium in nuclear power plants
- Nuclear weapons
- High-energy particle collisions in particle accelerators
Mass Defect & Binding Energy
- Experiments into nuclear structure have found that the total mass of a nucleus is less than the sum of the masses of its constituent nucleons
- This difference in mass is known as the mass defect
- Mass defect is defined as:
The difference between an atom's mass and the sum of the masses of its protons and neutrons
- The mass defect Δm of a nucleus can be calculated using:
Δm = Zmp + (A – Z)mn – mtotal
- Where:
- Z = proton number
- A = nucleon number
- mp = mass of a proton (kg)
- mn = mass of a neutron (kg)
- mtotal = measured mass of the nucleus (kg)
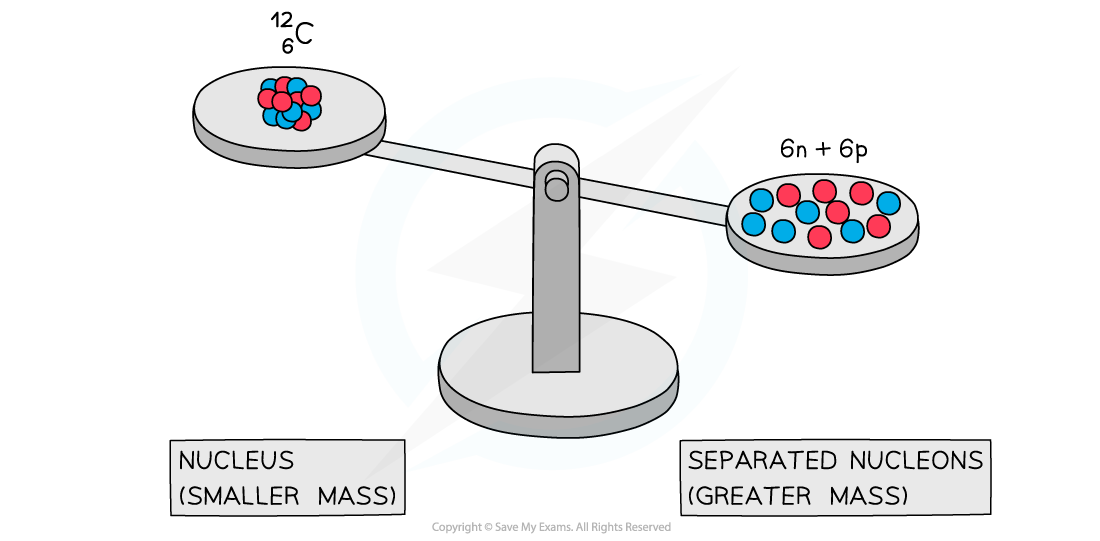
A system of separated nucleons has a greater mass than a system of bound nucleons
- Due to the equivalence of mass and energy, this decrease in mass implies that energy is released in the process
- Since nuclei are made up of neutrons and protons, there are forces of repulsion between the positive protons
- Therefore, it takes energy, ie. the binding energy, to hold nucleons together as a nucleus
- Binding energy is defined as:
The energy released when a nucleus forms from constituent nucleons
OR
The (minimum) energy needed to break a nucleus up into its constituent nucleons (protons and neutrons)
- Energy and mass are proportional, so, the total energy of a nucleus is less than the sum of the energies of its constituent nucleons
- The formation of a nucleus from a system of isolated protons and neutrons is therefore an exothermic reaction - meaning that it releases energy
- This can be calculated using the equation:
E = Δmc2
Exam Tip
Avoid describing the binding energy as the energy stored in the nucleus – this is not correct – it is energy that must be put into the nucleus to pull it apart.
Calculating Mass Defect & Nuclear Binding Energy
- Binding energy can often be described per nucleon
- This is simply found by dividing the relevant binding energy by the number of nucleons in the nucleus
Worked Example
The binding energy per nucleon is 7.98 MeV for an atom of Oxygen-16 (16O).
Determine an approximate value for the energy required, in MeV, to completely separate the nucleons of this atom.
Step 1: List the known quantities
-
- Binding energy per nucleon, E = 7.98 MeV
Step 2: State the number of nucleons
-
- The number of nucleons is 8 protons and 8 neutrons, therefore 16 nucleons in total
Step 3: Find the total binding energy
-
- The binding energy for oxygen-16 is:
7.98 × 16 = 127.7 MeV
Step 4: State the final answer
-
- The approximate total energy needed to completely separate this nucleus is 127.7 MeV
Worked Example
Calculate the binding energy per nucleon, in MeV, for the radioactive isotope potassium-40 (19K).
You may use the following data:
- Nuclear mass of potassium-40 = 39.953 548 u
- Mass of one neutron = 1.008 665 u
- Mass of one proton = 1.007 276 u
Step 1: Identify the number of protons and neutrons in potassium-40
-
- Proton number, Z = 19
- Neutron number, N = 40 – 19 = 21
Step 2: Calculate the mass defect, Δm
-
- Proton mass, mp= 1.007 276 u
- Neutron mass, mn= 1.008 665 u
- Mass of potassium-40, mtotal= 39.953 548 u
Δm = Zmp + Nmn – mtotal
Δm = (19 × 1.007276) + (21 × 1.008665) – 39.953 548
Δm = 0.36666 u
Step 3: Convert mass units from u to kg
-
- 1 u = 1.661 × 10–27 kg
Δm = 0.36666 × (1.661 × 10–27) = 6.090 × 10–28 kg
Step 4: Write down the equation for mass-energy equivalence
E = Δmc2
-
- Where c = 3.0 × 108 m s–1
Step 5: Calculate the binding energy, E
E = 6.090 × 10–28 × (3.0 × 108)2 = 5.5 × 10–11 J
Step 6: Determine the binding energy per nucleon and convert J to MeV
-
- Take the binding energy and divide it by the number of nucleons
- 1 MeV = 1.6 × 10–13 J
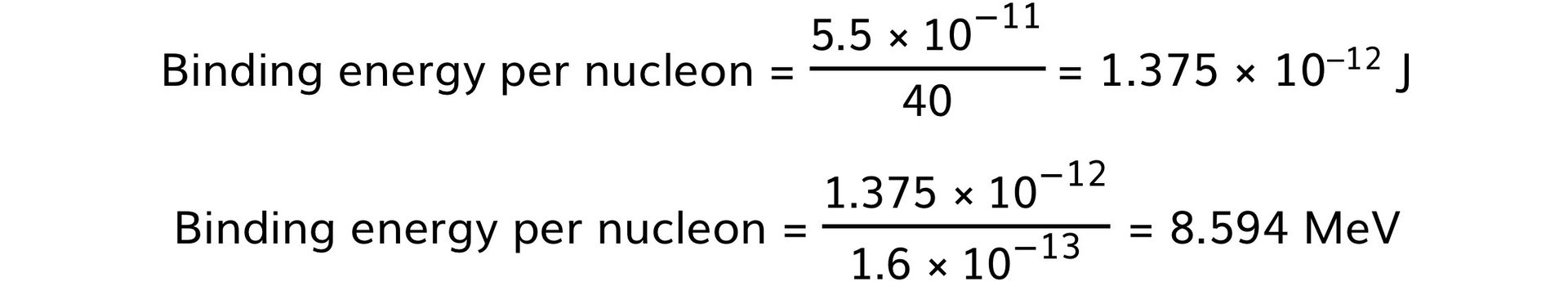
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





