- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
AQA A Level Maths: Pure复习笔记3.2.3 Bisection of Chords
Bisection of Chords
How can I find the equation of a perpendicular bisector?
- The perpendicular bisector of a line segment:
- is perpendicular to the line segment
- goes through the midpoint of the line segment

- The midpoint and gradient of the line segment between points (x1, y1) and (x2, y2) are given by the formulae

- The gradient of the perpendicular bisector is therefore

- The equation of the perpendicular bisector is the equation of the line with that gradient through the line segment's midpoint (see Equation of a Straight Line)
How can I use perpendicular bisectors to find the equation of a circle?
- A chord of a circle is a straight line segment between any two points on the circle

- The perpendicular bisector of a chord always goes through the centre of the circle

- If you know three points on a circle, draw two chords between them – the perpendicular bisectors of the chords will meet at the centre of the circle
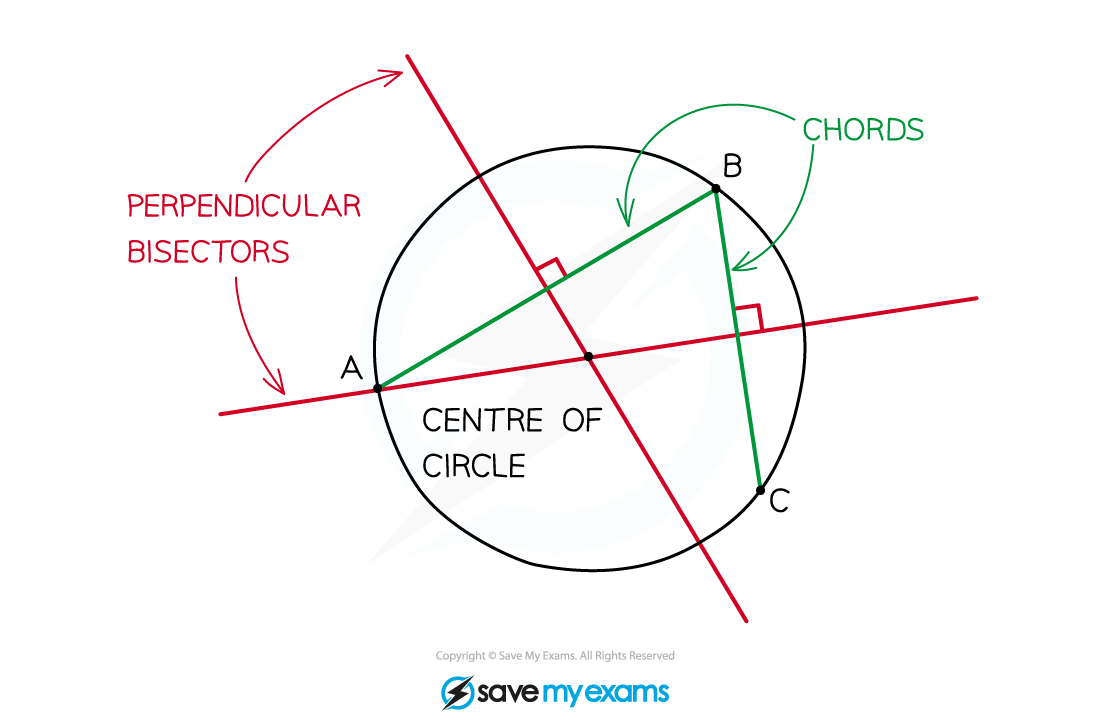
- Now that you know the centre of the circle and a point on the circle you can write the equation of the circle
Exam Tip
- To find the point of intersection of two straight lines, set the equations of the lines equal to each other and solve.
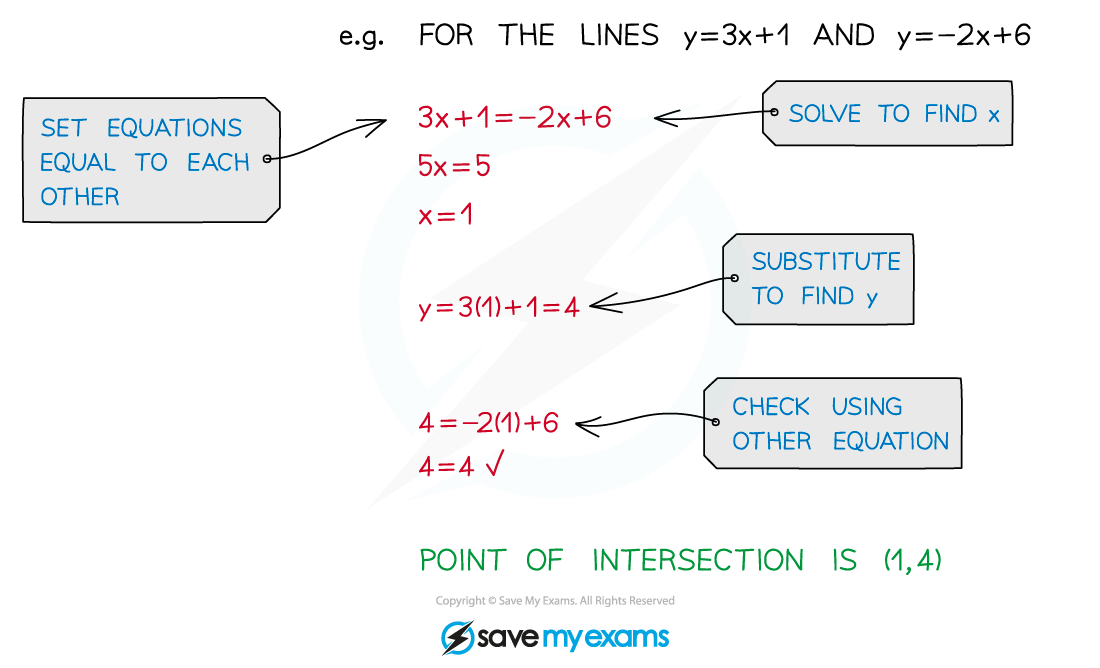
Worked Example

转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





