- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: HL复习笔记6.2.2 Circular Orbits
Circular Orbits
- Since most planets and satellites have a near circular orbit, the gravitational force FG between the sun or another planet provides the centripetal force needed to stay in an orbit
- Both the gravitational force and centripetal force are perpendicular to the direction of travel of the planet
- Consider a satellite with mass m orbiting Earth with mass M at a distance r from the centre travelling with linear speed v
FG = Fcirc
- Equating the gravitational force to the centripetal force for a planet or satellite in orbit gives:
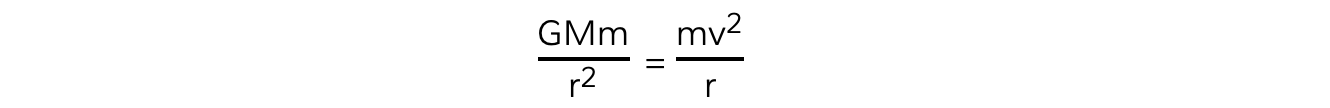
- The mass of the satellite m will cancel out on both sides to give:
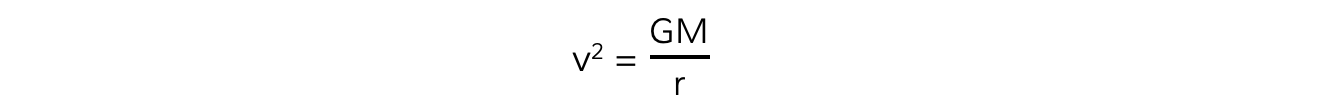
- Where:
- v = linear speed of the mass in orbit (m s-1)
- G = Newton's Gravitational Constant
- M = mass of the object being orbited (kg)
- r = orbital radius (m)
- This means that all satellites, whatever their mass, will travel at the same speed v in a particular orbit radius r
- Recall that since the direction of a planet orbiting in circular motion is constantly changing, it has centripetal acceleration
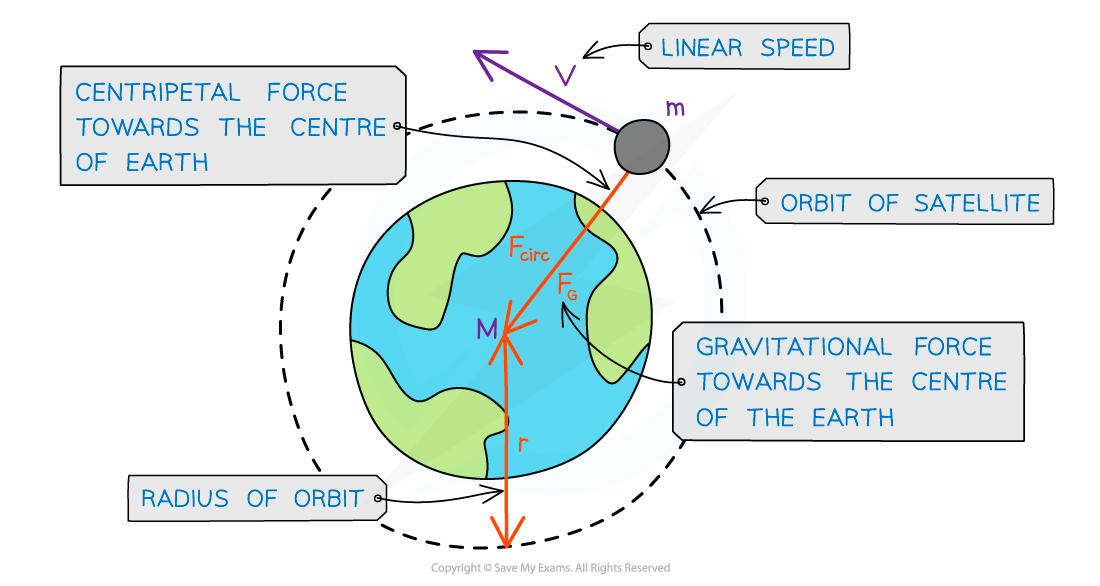
A satellite in orbit around the Earth travels in circular motion
Time Period & Orbital Radius Relation
- Since a planet or a satellite is travelling in circular motion when in order, its orbital time period T to travel the circumference of the orbit 2πr, the linear speed v is:
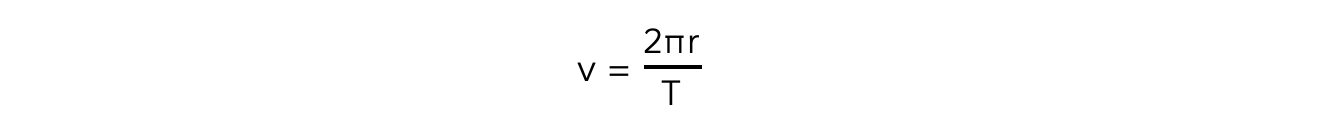
- This is a result of the well-known equation, speed = distance / time and first introduced in the circular motion topic
- Substituting the value of the linear speed v from equating the gravitational and centripetal force into the above equation gives:
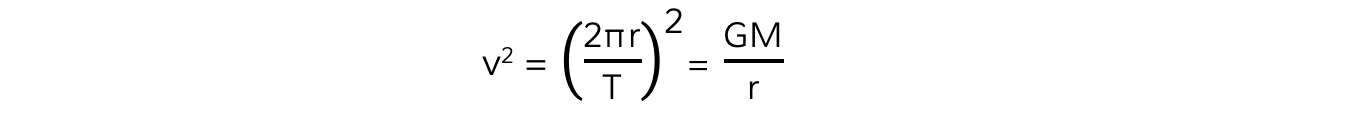
- Squaring out the brackets and rearranging for T2 gives the equation relating the time period T and orbital radius r:
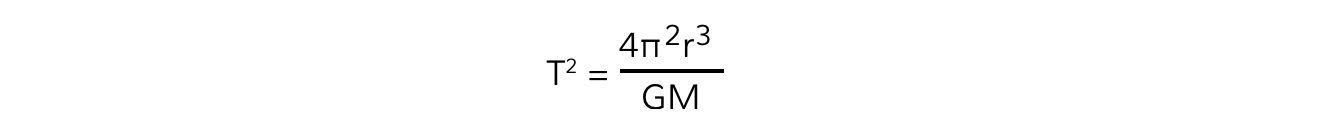
- Where:
- T = time period of the orbit (s)
- r = orbital radius (m)
- G = Newton's Gravitational Constant
- M = mass of the object being orbited (kg)
- The equation shows that the orbital period T is related to the radius r of the orbit. This is also known as Kepler’s third law:
For planets or satellites in a circular orbit about the same central body, the square of the time period is proportional to the cube of the radius of the orbit
- Kepler’s third law can be summarised as:
![]()
Graphical Representation of T2 ∝ r3
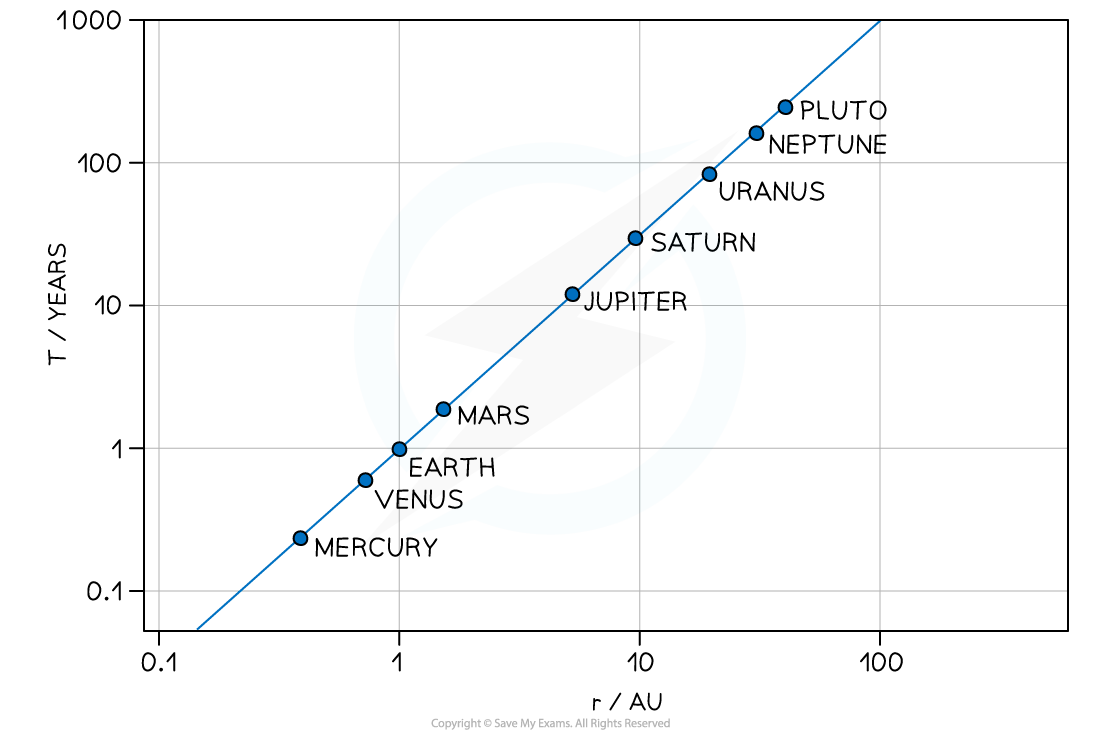
- The relationship between T and r can be shown using a logarithmic plot
- Plotting of T in years against r in AU (astronomical units) (for the planets in our solar system) on a log paper or taking logs and plotting on regular graph paper is a straight-line graph:
- The graph does not go through the origin since it has a negative y-intercept
Maths Tip
- The ∝ symbol means ‘proportional to’
- Find out more about proportional relationships between two variables in the “proportional relationships ” section of the A Level Maths revision notes
Worked Example
A binary star system constant of two stars orbiting about a fixed point B.The star of mass M1 has a circular orbit of radius R1 and mass M2 has a radius of R2. Both have linear speed v and an angular speed ⍵ about B.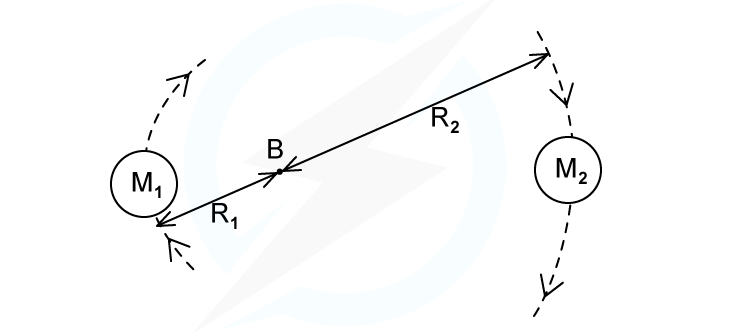
State the following formula, in terms of G, M2, R1 and R2
(i) The angular speed ⍵ of M1
(ii) The time period T for each star in terms of angular speed ⍵


Exam Tip
Many of the calculations in the Gravitation questions depend on the equations for circular motion. Be sure to revisit these and understand how to use them!You will be expected to remember the derivation for T2 ∝ r3 relation, so make sure you understand each step
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





