- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: HL复习笔记6.1.4 Applications of Circular Motion
Applications of Circular Motion
Horizontal Circular Motion
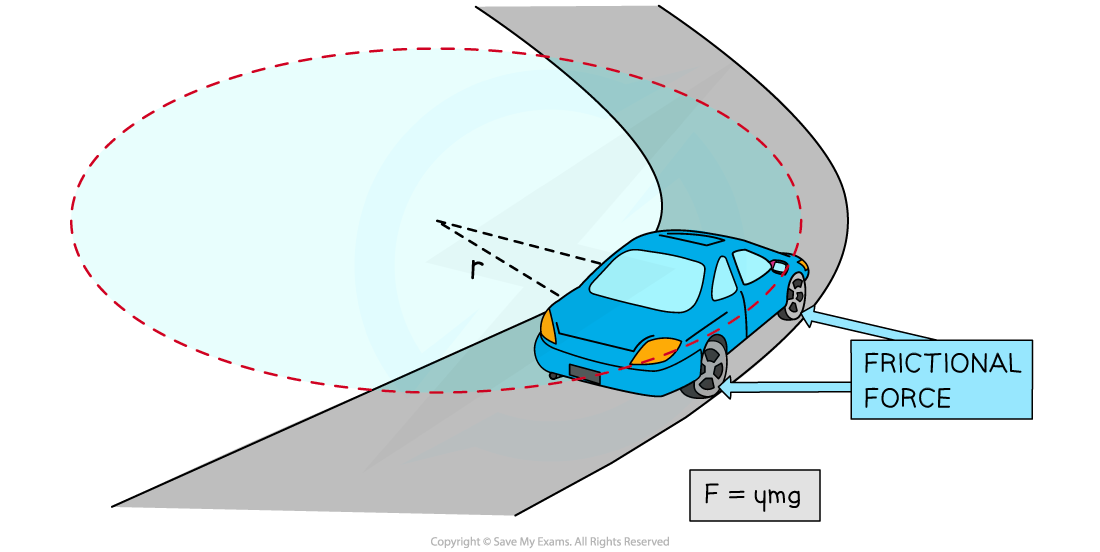
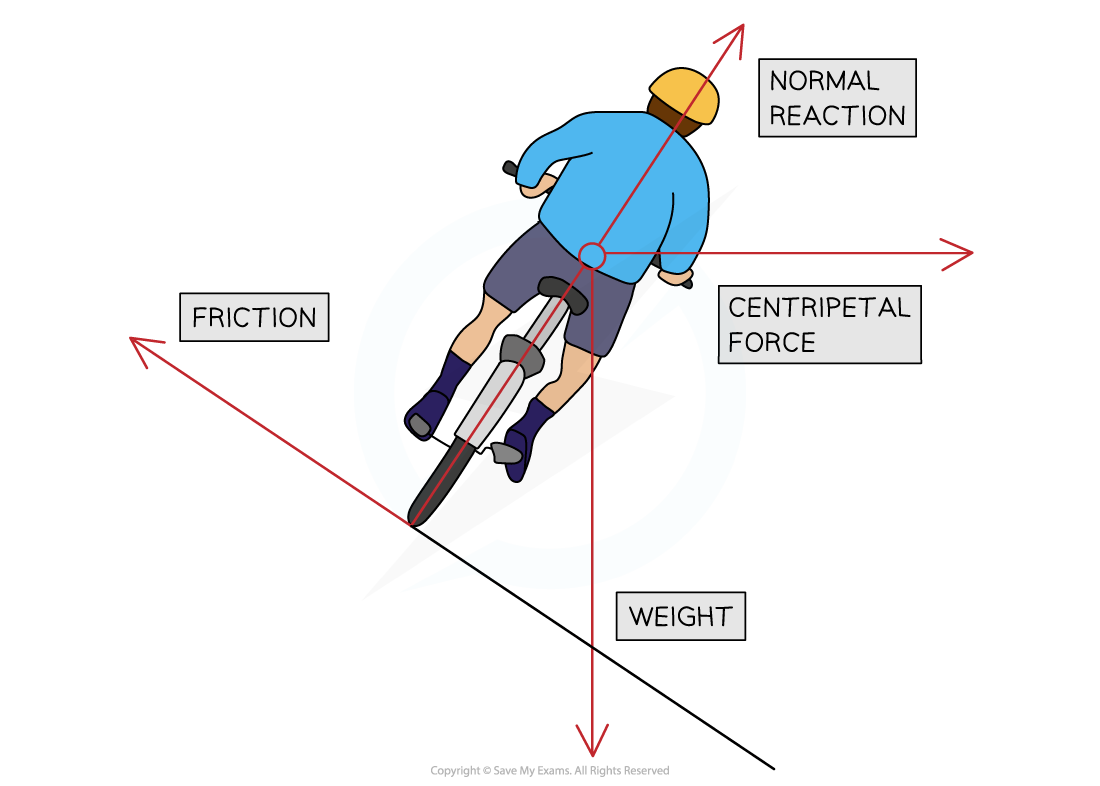
- An example of horizontal circular motion is a vehicle driving on a curved road
- The forces acting on the vehicle are:
- The friction between the tyres and the road
- The weight of the vehicle downwards
- In this case, the centripetal force required to make this turn is provided by the frictional force
- This is because the force of friction acts towards the centre of the circular path
- Since the centripetal force is provided by the force of friction, the following equation can be written:
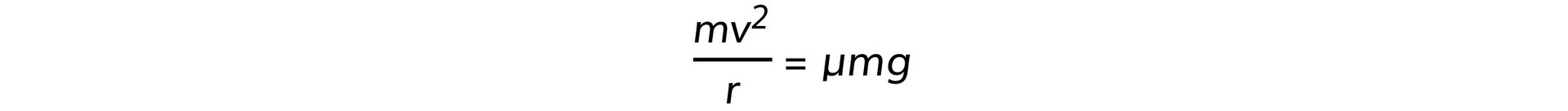
- Where:
- m = mass of the vehicle (kg)
- v = speed of the vehicle (m s–1)
- r = radius of the circular path (m)
- μ = static coefficient of friction
- g = acceleration due to gravity (m s–2)
- Rearranging this equation for v gives:
v2 = μgr
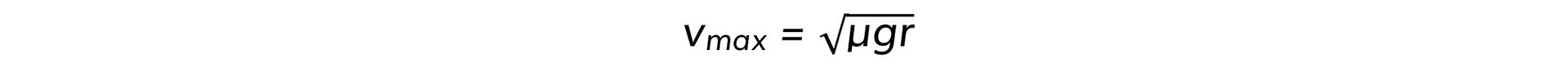
- This expression gives the maximum speed at which the vehicle can travel around the curved road without skidding
- If the speed exceeds this, then the vehicle is likely to skid
- This is because the centripetal force required to keep the car in a circular path could not be provided by friction, as it would be too large
- Therefore, in order for a vehicle to avoid skidding on a curved road of radius r, its speed must satisfy the equation
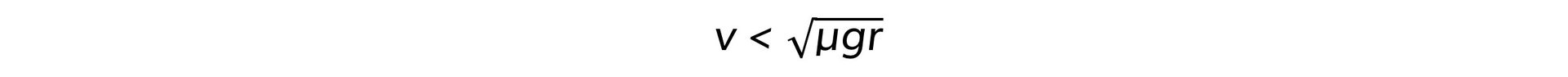
Banking
- A banked road, or track, is a curved surface where the outer edge is raised higher than the inner edge
- The purpose of this is to make it safer for vehicles to travel on the curved road, or track, at a reasonable speed without skidding
- When a road is banked, the centripetal force no longer depends on the friction between the tyres and the road
- Instead, the centripetal force depends solely on the normal force and the weight of the vehicle
Vertical Circular Motion
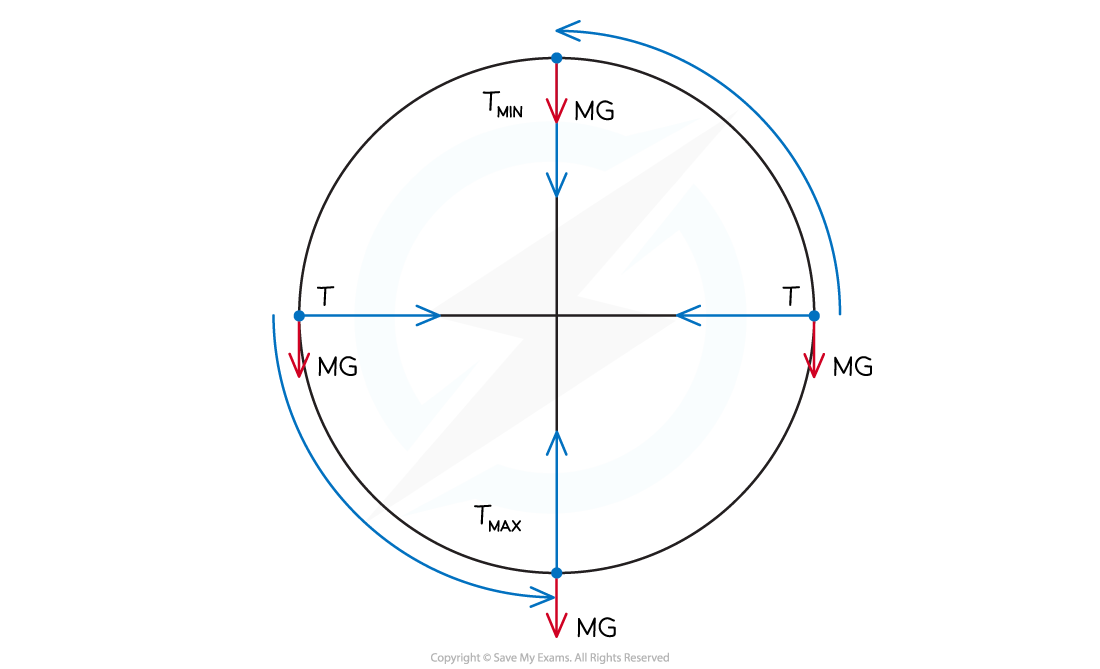
- An example of vertical circular motion is swinging a ball on a string in a vertical circle
- The forces acting on the ball are:
- The tension in the string
- The weight of the ball downwards
- As the ball moves around the circle, the direction of the tension will change continuously
- The magnitude of the tension will also vary continuously, reaching a maximum value at the bottom and a minimum value at the top
- This is because the direction of the weight of the ball never changes, so the resultant force will vary depending on the position of the ball in the circle
- At the bottom of the circle, the tension must overcome the weight, this can be written as:
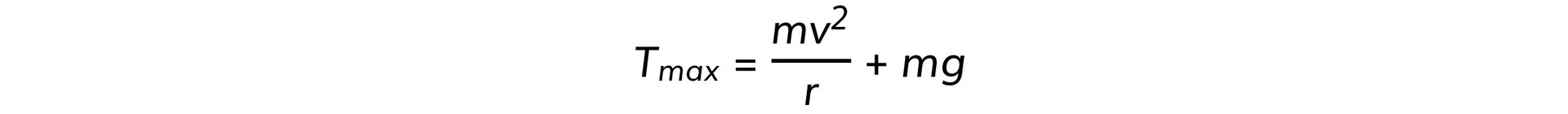
- As a result, the acceleration, and hence, the speed of the ball will be slower at the top
- At the top of the circle, the tension and weight act in the same direction, this can be written as:
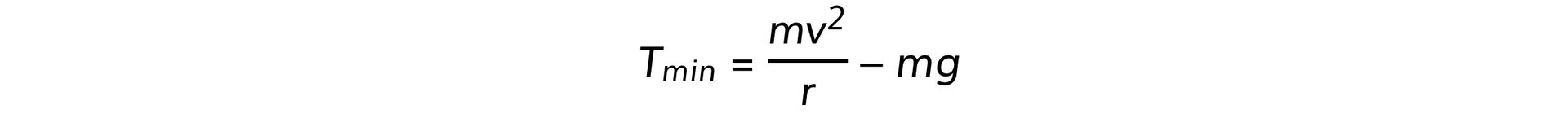
- As a result, the acceleration, and hence, the speed of the ball will be faster at the bottom
Exam Tip
You do not need to know the mathematics of banking but you may be required to explain the principles unpinning it, so make sure you understand it!
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





