- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: HL复习笔记6.1.2 Centripetal Force
Centripetal Force
- An object moving in a circle is not in equilibrium, it has a resultant force acting upon it
- This is known as the centripetal force and is what keeps the object moving in a circle
- The centripetal force (F) is defined as:
The resultant force perpendicular to the velocity, and therefore directed towards the centre of the circle, required to keep a body in uniform circular motion
- The magnitude of the centripetal force F can be calculated using:
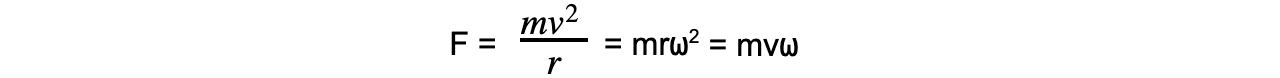
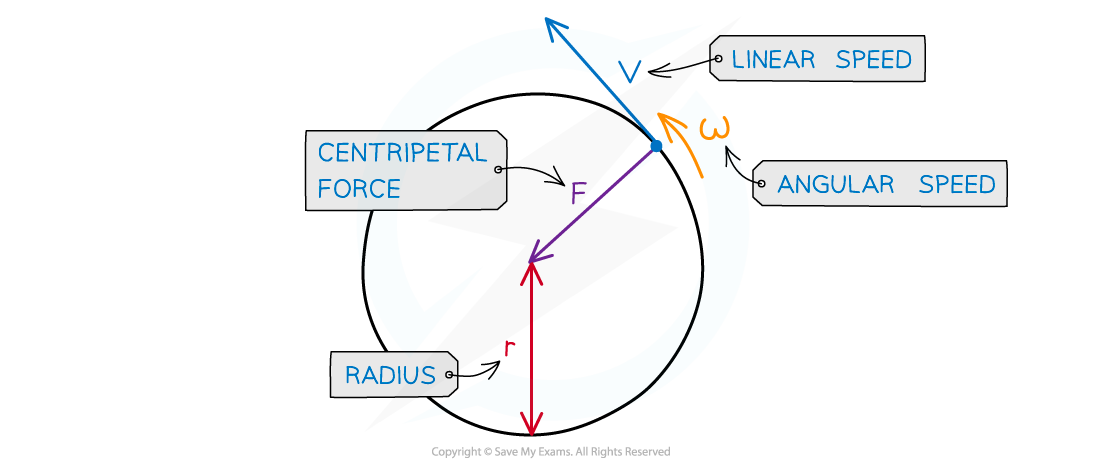
Centripetal force is always perpendicular to the linear velocity (i.e., the direction of travel)
- Where:
- F = centripetal force (N)
- v = linear speed (m s−1)
- ⍵ = angular speed (rad s−1)
- r = radius of the orbit (m)
- Note: centripetal force and centripetal acceleration act in the same direction
- This is due to Newton's Second Law
- The centripetal force is not a separate force of its own
- It can be any type of force, depending on the situation, which keeps an object moving in a circular path
- For example, tension, friction, gravitational, electrical or magnetic
Examples of centripetal force
- When solving circular motion problems involving one of these forces, the equation for centripetal force can be equated to the relevant force equation
- For example, for a charged particle travelling in a circle, the centripetal force causing the charged particle to move in a circle is provided by the magnetic force
- Therefore, equating the expressions for centripetal force and magnetic force gives the following:
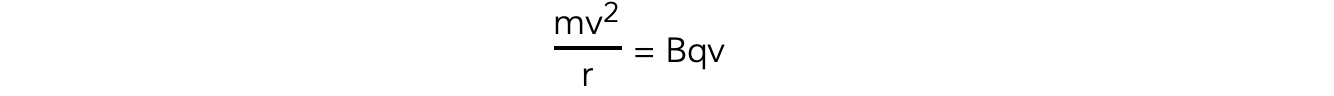
- Where:
- B = magnetic field strength (T)
- q = charge on the particle (C)
- m = mass of the particle (kg)
- v = speed of the particle (m s−1)
- r = radius of orbit (m)
A bucket of mass 8.0 kg is filled with water is attached to a string of length 0.5 m.What is the minimum speed the bucket must have at the top of the circle so no water spills out?
Step 1: Draw the forces on the bucket at the top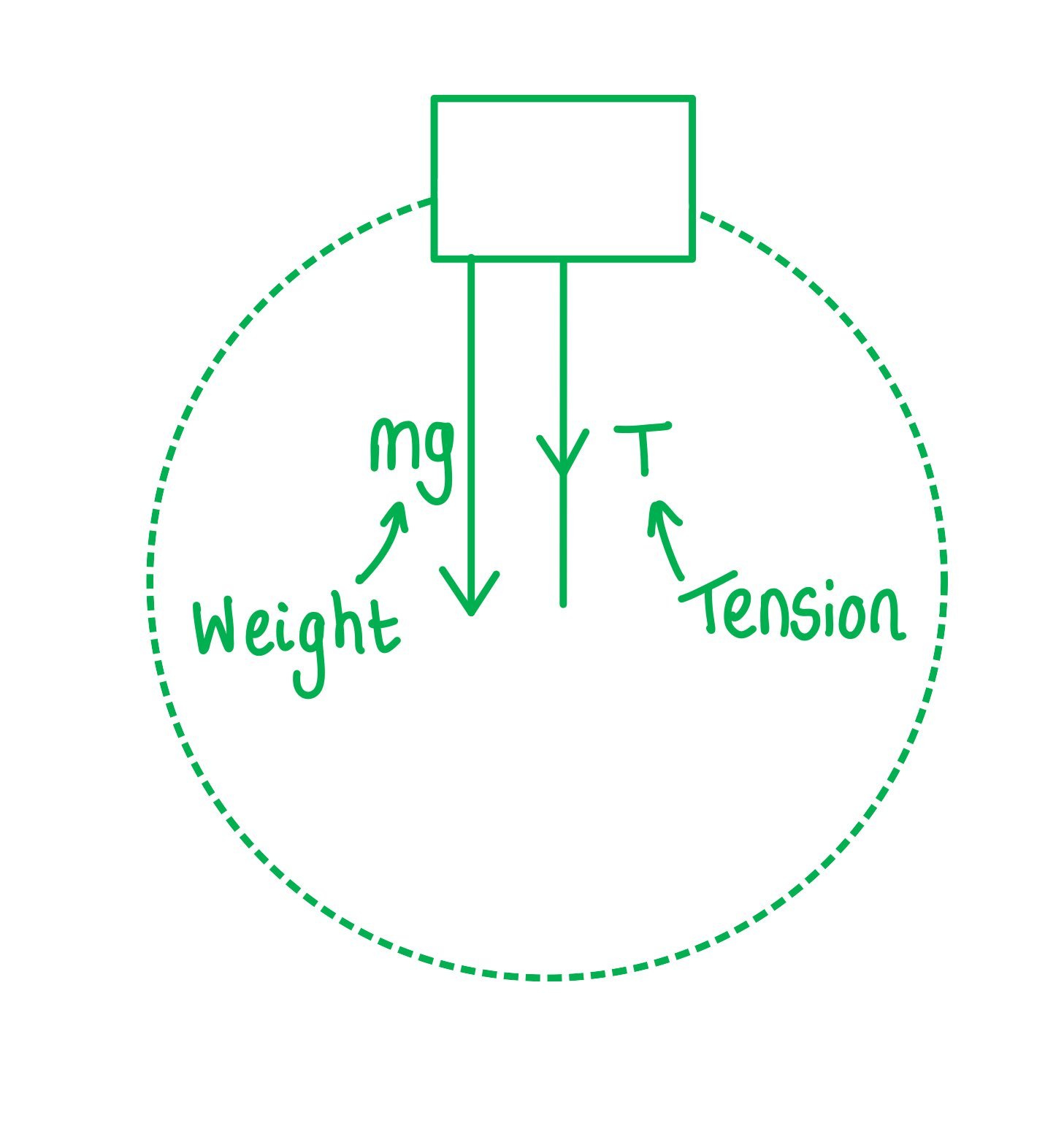
Step 2: Calculate the centripetal force
-
- The weight of the bucket = mg
- This is equal to the centripetal force since it is directed towards the centre of the circle
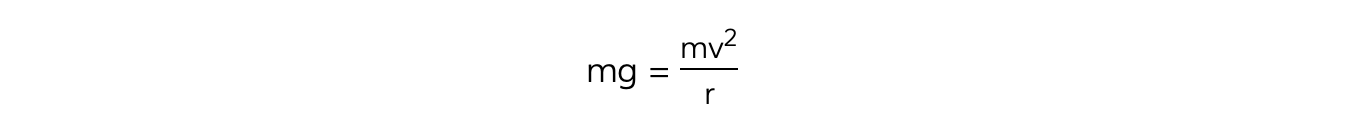
Step 3: Rearrange for velocity v
-
- m cancels from both sides
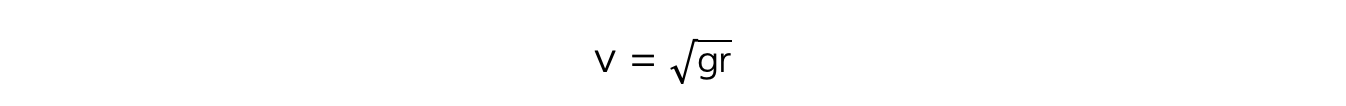 Step 4: Substitute in values
Step 4: Substitute in values
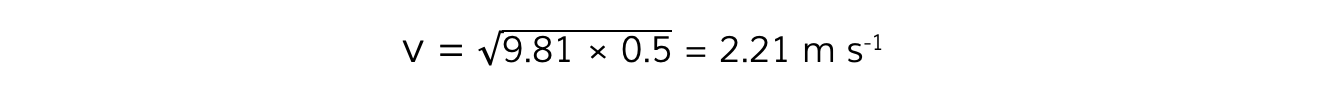
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





