- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: HL复习笔记5.4.4 Solving Problems Involving Magnetic Forces
Solving Problems Involving Magnetic Forces
- There is a lot of mathematics surrounding magnetism and magnetic forces
- The key equations are:
Force on a current-carrying conductor:
F = BIL
F = BIL
Force on a moving charge:
F = Bqv
F = Bqv
Radius of a moving charge in a magnetic field:
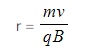
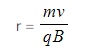
- Below are two worked examples demonstrating different situations involving magnetic forces
Worked Example
A 5 cm length of wire is at 90° to the direction of an external magnetic field. When a current of 1.5 A flows through the wire it experiences a force of 0.06 N from the motor effect.
Calculate the magnetic flux density of the magnet.
Step 1: List the known quantities
- Length, L = 5 cm = 0.05 m
- Current, I = 1.5 A
- Force, F = 0.06 N
Step 2: Write out the equation for magnetic force
F = BIL
Step 3: Rearrange the equation to make B the subject
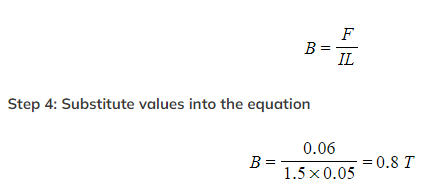
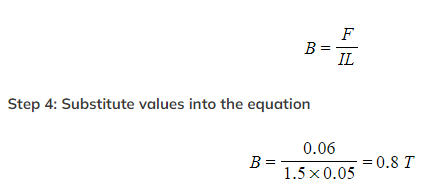
Worked Example
This question is about the movement of an electrically charged particle into a magnetic field. An electron enters a magnetic field and moves in an approximately circular path as shown below.
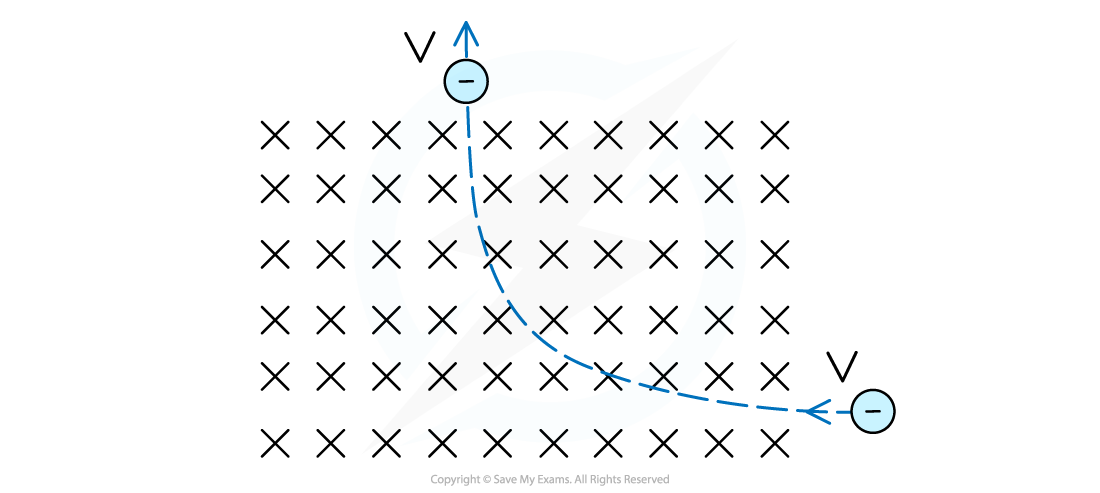
- Explain whether the speed of the proton is the same when entering and exiting the magnetic field.
- The magnetic field has a strength of 0.3 T and the velocity of the electron before entering the magnetic field is 8.6 × 106 m s−1 to the left. Show that the radius of the motion of the electrons is 1.63 cm.
Part (a)
-
-
The answer is that the work done by the magnetic force on the charge must be zero
-
This is because the force itself is at right angles to the velocity
-
Since the work done is zero, therefore the kinetic energy does not change between entering and leaving the magnetic field
-
Therefore the speed is the same
-
Part (b)
Step 1: List the known quantities
- Magnetic field strength, B = 0.3 T
- Velocity of electron (before entering field), v = 8.6 × 106 m s−1 to the left
- Radius of motion to be shown, r = 1.63 cm
Step 2: Equate the magnetic force and the force of circular motion
- This can be done for the situation since the circular motion is caused by the magnetic force
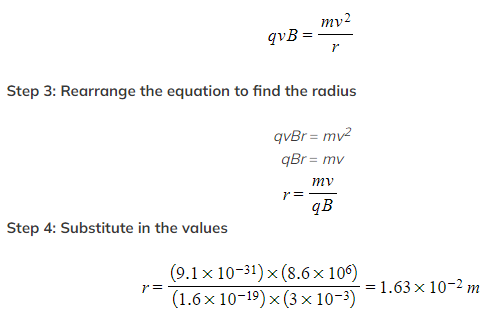 Step 5: State final answer
Step 5: State final answerR = 1.63 × 10−2 m = 1.63 cm in a circular motion
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





