- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
AQA A Level Physics复习笔记3.3.5 Required Practical: Young's Slit Experiment & Diffraction Gratings
Required Practical: Young's Slit Experiment & Diffraction Gratings
Equipment List

- Resolution of measuring equipment:
- Metre ruler = 1 mm
- Vernier Callipers = 0.01 mm
Young’s Double-Slit Experiment
The overall aim of this experiment is to investigate the relationship between the distance between the slits and the screen, D, and the fringe width, w
- Independent variable = Fringe width, w
- Dependent variable = Distance between the slits and the screen, D
- Control variables
- Laser wavelength, λ
- Slit separation, s
Method
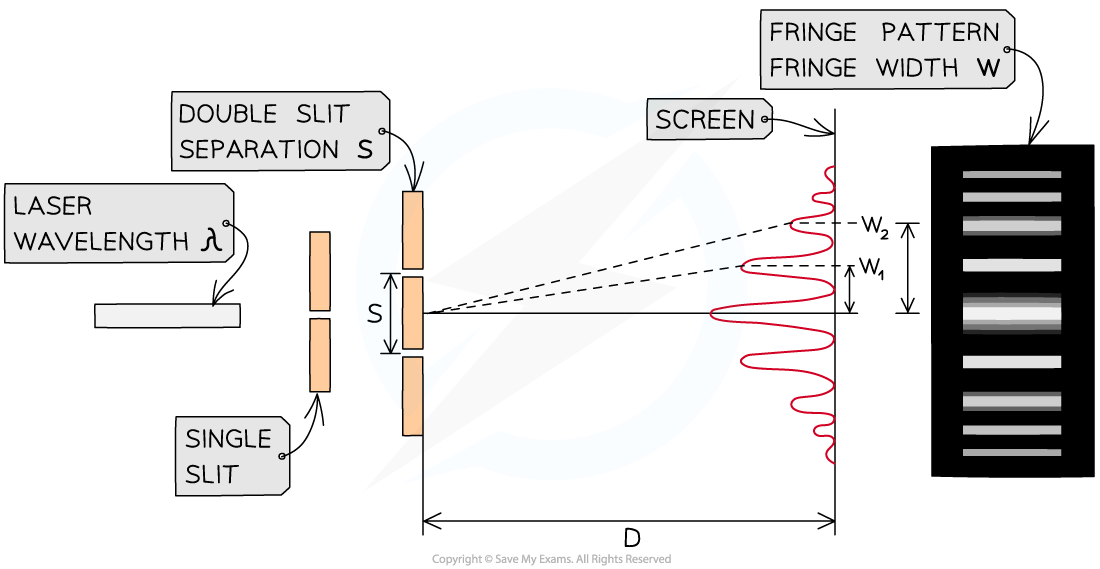
The setup of apparatus required to measure the fringe width w for different values of D
- Set up the apparatus by fixing the laser and the slits to a retort stand and place the screen so that D is 0.5 m, measured using the metre ruler
- Darken the room and turn on the laser
- Measure from the central fringe across many fringes using the vernier callipers and divide by the number of fringe widths to find the fringe width, w
- Increase the distance D by 0.1 m and repeat the procedure, increasing it by 0.1 m each time up to around 1.5 m
- Repeat the experiment twice more and calculate and record the mean fringe width w for each distance D
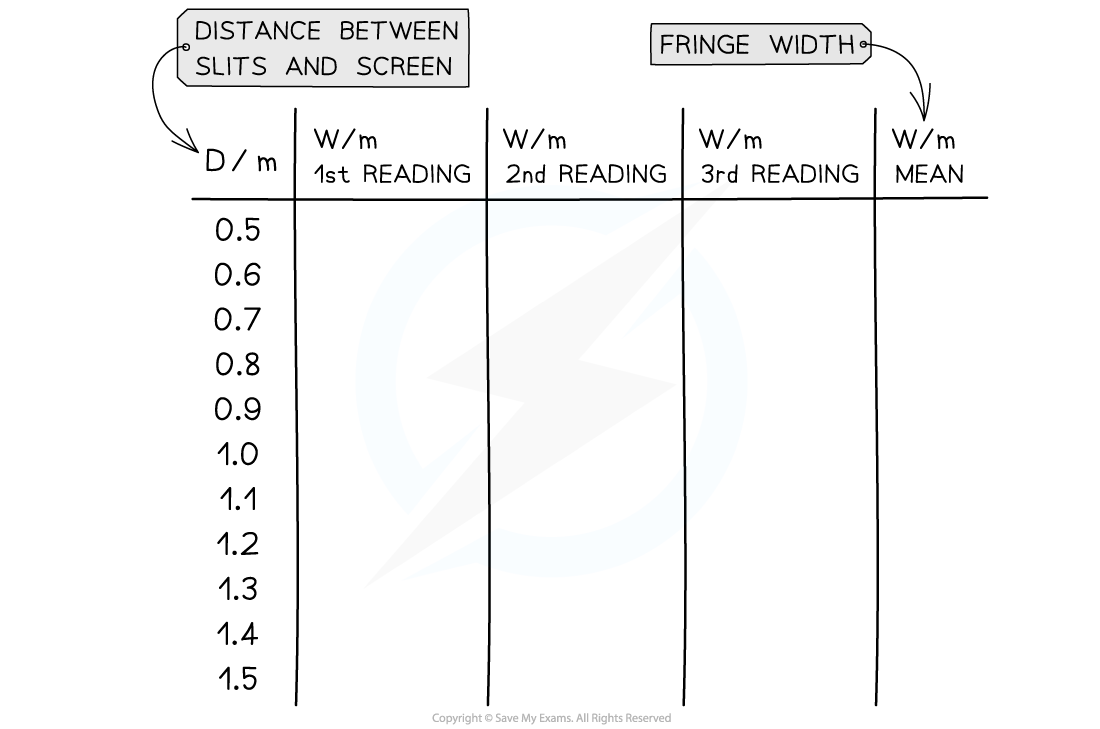
- An example table might look like this:
Analysing the Results
- The fringe spacing equation is given by:
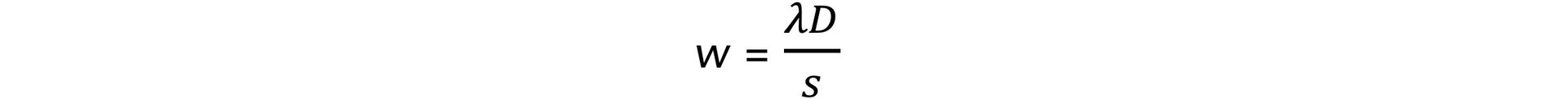
- Where:
- w = the distance between each fringe (m)
- λ = the wavelength of the laser light (m)
- D = the distance between the slit and the screen (m)
- s = the slit separation (m)
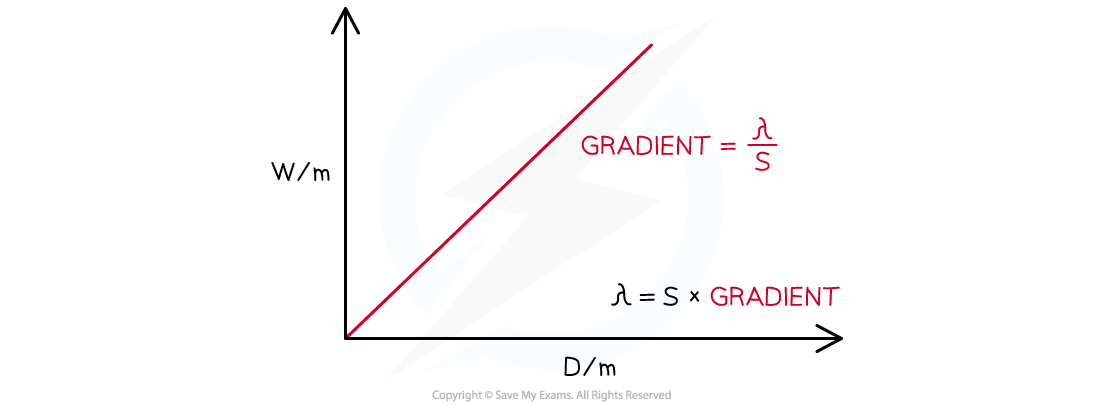
- Comparing this to the equation of a straight line: y = mx
- y = w (m)
- x = D (m)
- Gradient = λ/s (unitless)
- Plot a graph of w against D and draw a line of best fit
- The wavelength of the laser light is equal to the gradient multiplied by the slit separation, because:
Interference by a Diffraction Grating
The overall aim of this experiment is to calculate the wavelength of the laser light using a diffraction grating
- Independent variable = Distance between maxima, h
- Dependent variable = The angle between the normal and each order, θn (where n = 1, 2, 3 etc)
- Control variables
- Distance between the slits and the screen, D
- Laser wavelength λ
- Slit separation, d
Method
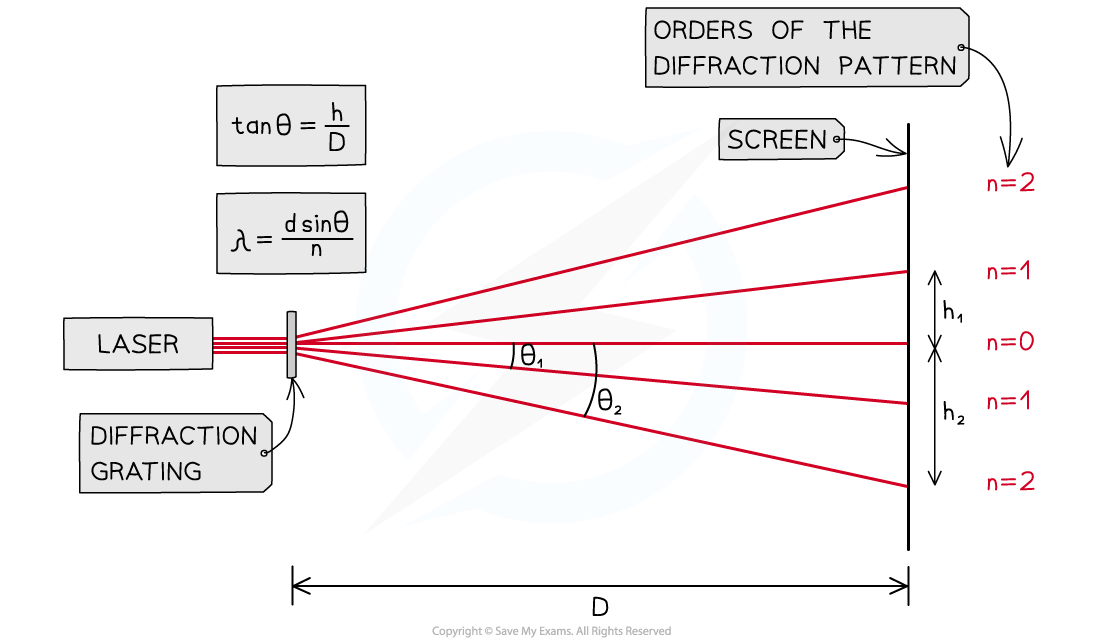
The setup of apparatus required to measure the distance between maxima h at different angles θ
- Place the laser on a retort stand and the diffraction grating in front of it
- Use a set square to ensure the beam passes through the grating at normal incidence and meets the screen perpendicularly
- Set the distance D between the grating and the screen to be 1.0 m using a metre ruler
- Darken the room and turn on the laser
- Identify the zero-order maximum (the central beam)
- Measure the distance h to the nearest two first-order maxima (i.e. n = 1, n = 2) using a vernier calliper
- Calculate the mean of these two values
- Measure distance h for increasing orders
- Repeat with a diffraction grating with a different number of slits per mm
- An example table might look like this:

Analysing the Results
The diffraction grating equation is given by:
nλ = d sin θ
- Where:
- n = the order of the diffraction pattern
- λ = the wavelength of the laser light (m)
- d = the distance between the slits (m)
- θ = the angle between the normal and the maxima
- The distance between the slits is equal to:
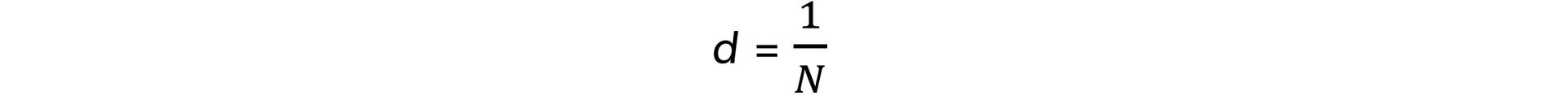
- Where
- N = the number of slits per metre (m–1)
- Since the angle is not small, it must be calculated using trigonometry with the measurements for the distance between maxima, h, and the distance between the slits and the screen, D

- Calculate a mean θ value for each order
- Calculate a mean value for the wavelength of the laser light and compare the value with the accepted wavelength
- This is usually 635 nm for a standard school red laser
Evaluating the Experiments
Systematic errors:
- Ensure the use of the set square to avoid parallax error in the measurement of the fringe width
- Using a grating with more lines per mm will result in greater values of h. This lowers its percentage uncertainty
Random errors:
- The fringe spacing can be subjective depending on its intensity on the screen, therefore, take multiple measurements of w and h (between 3-8) and find the average
- Use a Vernier scale to record distances w and h to reduce percentage uncertainty
- Reduce the uncertainty in w and h by measuring across all visible fringes and dividing by the number of fringes
- Increase the grating to screen distance D to increase the fringe separation (although this may decrease the intensity of light reaching the screen)
- Conduct the experiment in a darkened room, so the fringes are clear
Safety Considerations
- Lasers should be Class 2 and have a maximum output of no more than 1 mW
- Do not allow laser beams to shine into anyone’s eyes
- Remove reflective surfaces from the room to ensure no laser light is reflected into anyone’s eyes
Worked Example
A student investigates the interference patterns produced by two different diffraction gratings. One grating used was marked 100 slits / mm, the other was marked 300 slits / mm. The distance between the grating and the screen is measured to be 3.75 m.The student recorded the distance between adjacent maxima after passing a monochromatic laser source through each grating. These results are shown in the tables below.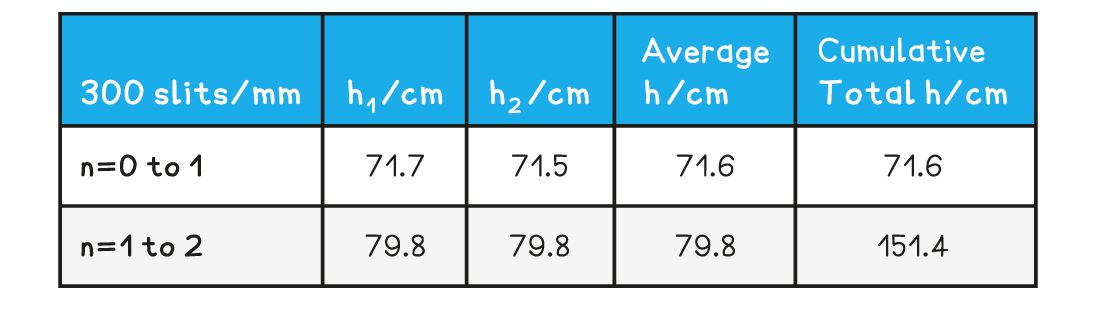
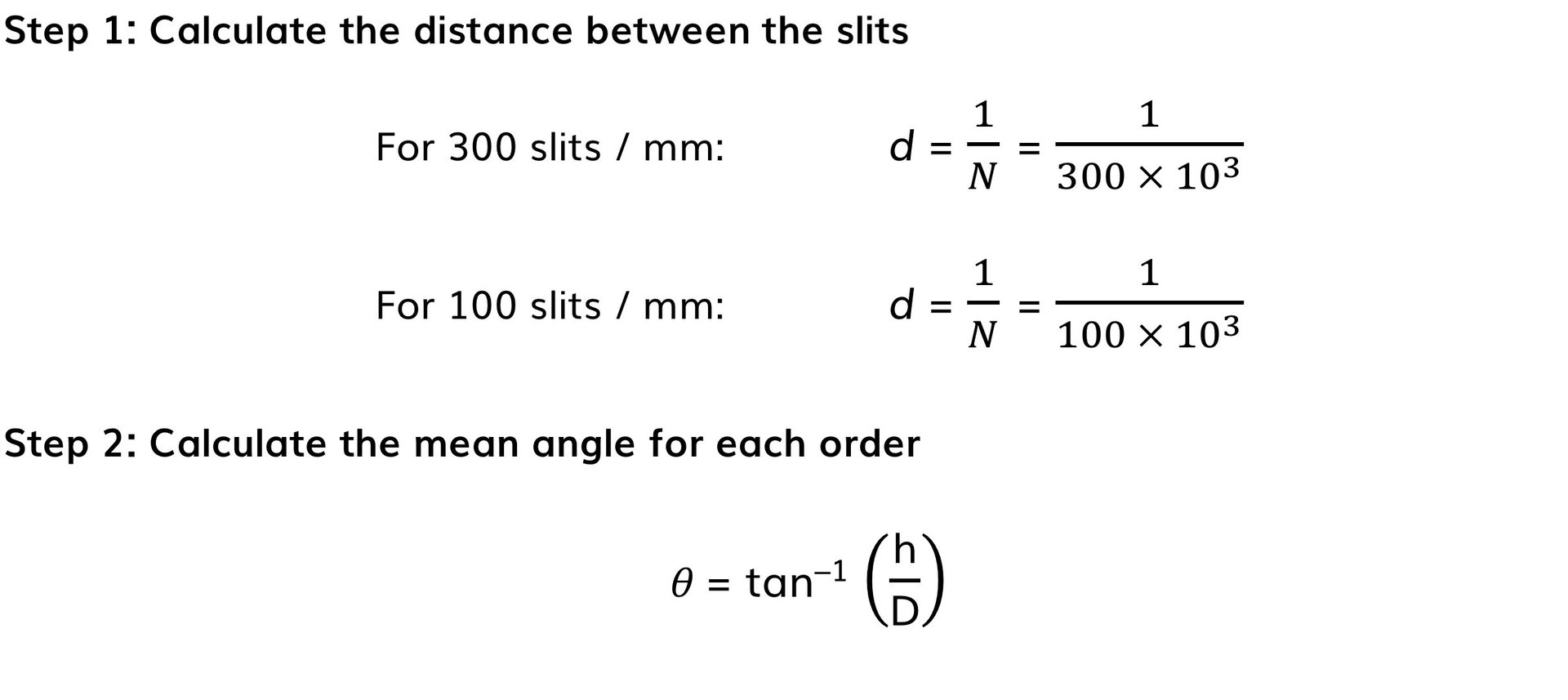
 Calculate the mean wavelength of the laser light and compare it with the accepted value of 635 nm. Assess the percentage uncertainty in this result.
Calculate the mean wavelength of the laser light and compare it with the accepted value of 635 nm. Assess the percentage uncertainty in this result.
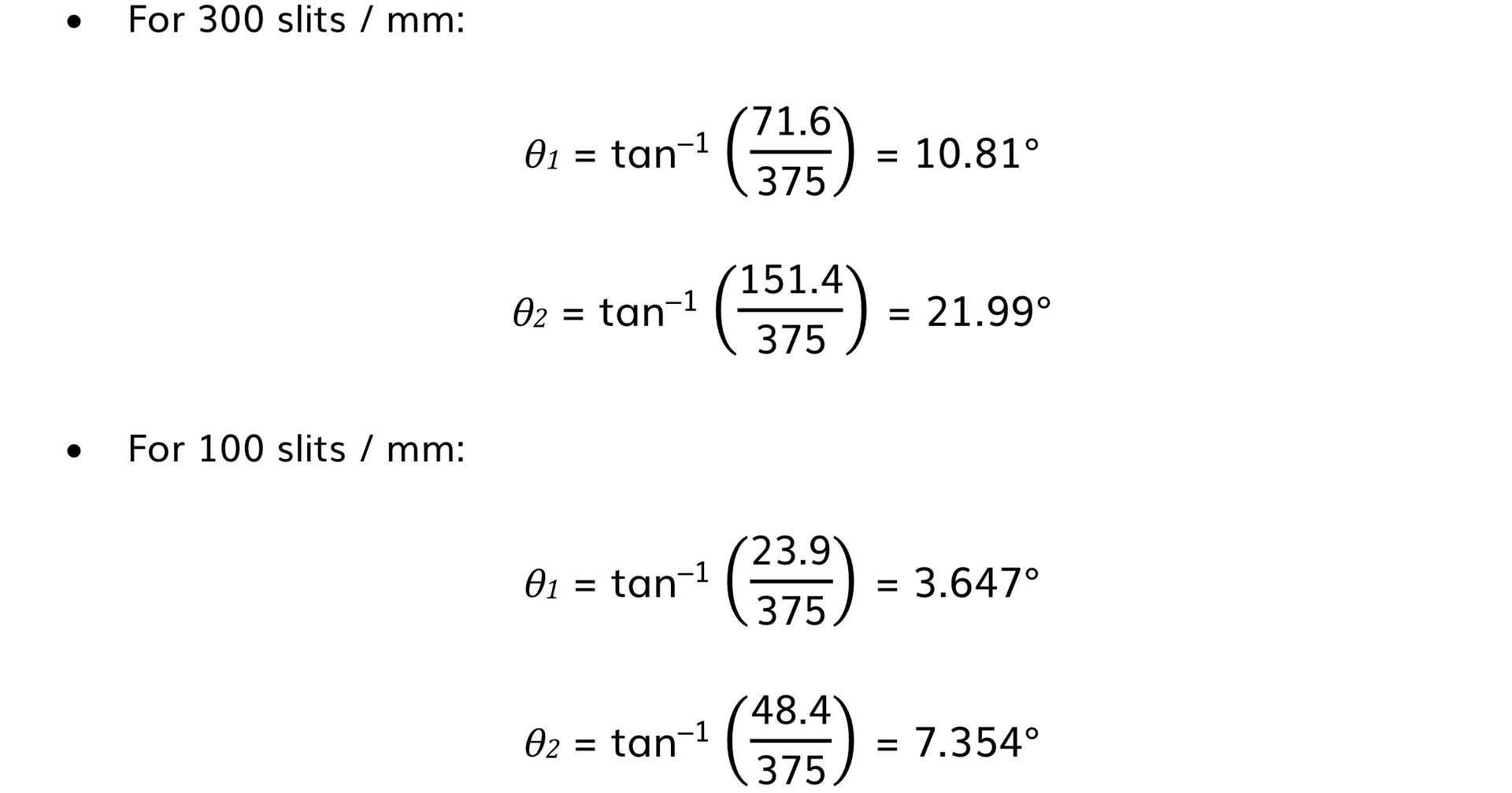


转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





