- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
AQA A Level Physics复习笔记2.5.5 Diffraction Effects of Momentum
Diffraction Effects of Momentum
- When electrons pass through a slit similar in size to themselves, they exhibit a wavelike property( Diffraction), meaning they spread out like a wave passing through a narrow gap
- The regular spacing of atoms in a crystalline solid act as a diffraction grating, scattering the electrons in a predictable manner
- The observed diffraction pattern can be used to deduce the structure of the crystal producing that pattern
- High energy electrons have a shorter wavelength and can therefore be used to look at the size of the nucleus of an atom as opposed to the arrangement of atoms in a crystal
- The de Broglie wavelength tells us about the wave-particle relationship:
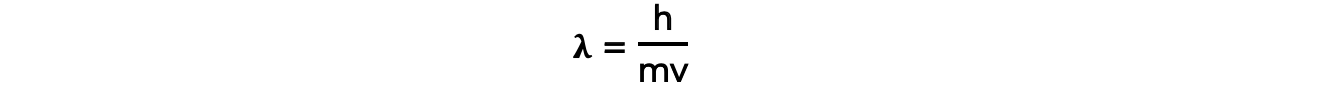
- Where:
- λ = the de Broglie wavelength (m)
- h = Planck’s Constant (J s)
- m = mass of the electron (kg)
- v = velocity of the electron (m s–1)
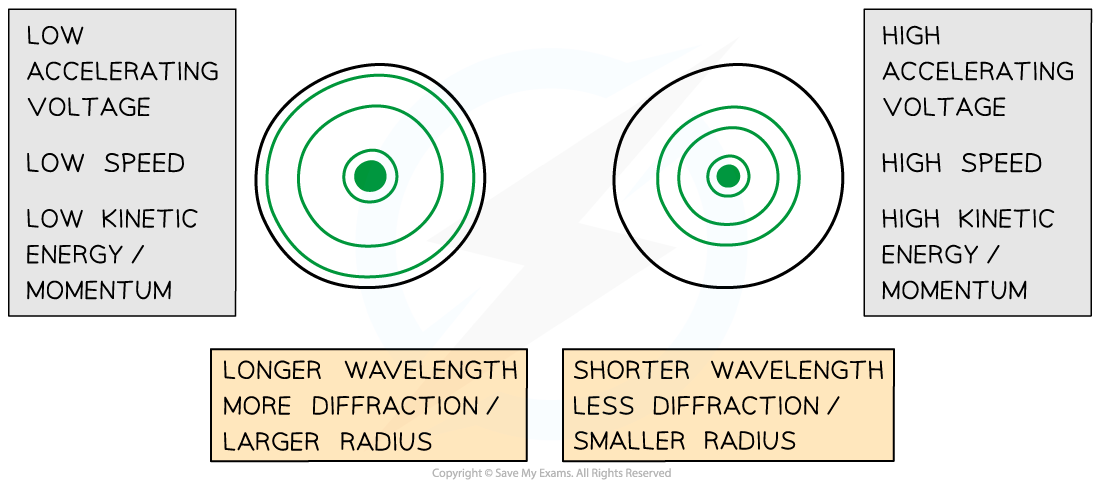
Comparison of electron diffraction patterns at different values of momentum
Momentum
- Momentum is equal to p = mv, so, from de Broglie's equation:
- A smaller momentum will result in a longer wavelength
- A larger momentum will result in a shorter wavelength
Kinetic Energy
- If the electron speed / kinetic energy is increased, by increasing the accelerating voltage, then:
- The wavelength of the wave will decrease
- The diffraction rings will appear closer together
- The higher the kinetic energy of the electron, the higher its momentum hence the smaller its wavelength
Radius of the Diffraction Pattern
- The radius of the diffraction pattern depends on the wavelength:
- The longer the wavelength, the more the light spreads out hence a larger radius is produced
- The shorter the wavelength, the smaller the radius produced
- Therefore, electrons with smaller momentum will produce a more diffuse diffraction pattern
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





