- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
AQA A Level Physics复习笔记2.5.4 The de Broglie Wavelength
The de Broglie Wavelength
- Using ideas based upon the quantum theory and Einstein’s theory of relativity, de Broglie suggested that the momentum (p) of a particle and its associated wavelength (λ) are related by the equation:
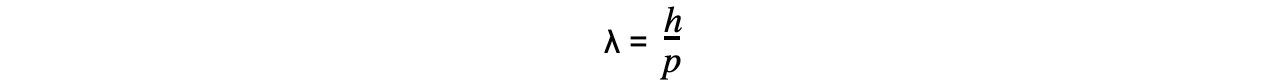
- Since momentum p = mv, the de Broglie wavelength can be related to the speed of a moving particle (v) by the equation:
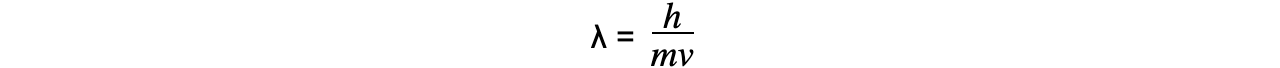
- Since kinetic energy E = ½ mv2
- Momentum and kinetic energy can be related by:
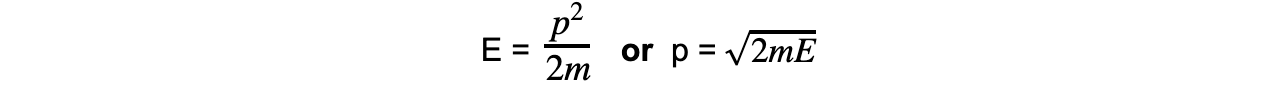
- Combining this with the de Broglie equation gives a form which relates the de Broglie wavelength of a particle to its kinetic energy:
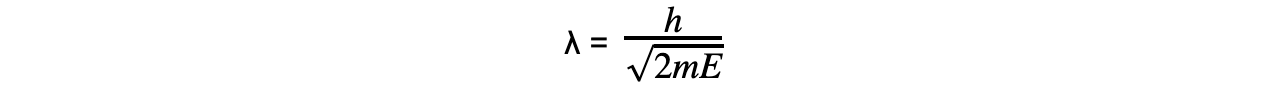
- Where:
- λ = the de Broglie wavelength (m)
- h = Planck’s constant (J s)
- p = momentum of the particle (kg m s-1)
- E = kinetic energy of the particle (J)
- m = mass of the particle (kg)
- v = speed of the particle (m s-1)
Worked Example
A proton and an electron are each accelerated from rest through the same potential difference.
Determine the ratio: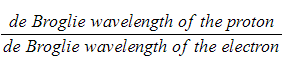

转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





