- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
AQA A Level Physics复习笔记2.5.2 Energy Levels & Photon Emission
Line Spectra & Energy Levels
Atomic Energy Levels
- Electrons in an atom can have only certain specific energies
- These energies are called electron energy levels
- They can be represented as a series of stacked horizontal lines increasing in energy
- Normally, electrons occupy the lowest energy level available, this is known as the ground state
- Electrons can gain energy and move up the energy levels if it absorbs energy either by:
- Collisions with other atoms or electrons
- Absorbing a photon
- A physical source, such as heat
- This is known as excitation, and when electrons move up an energy level, they are said to be in an excited state
- If the electron gains enough energy to be removed from the atom entirely, this is known as ionisation
- When an electron returns to a lower energy state from a higher excited state, it releases energy in the form of a photon
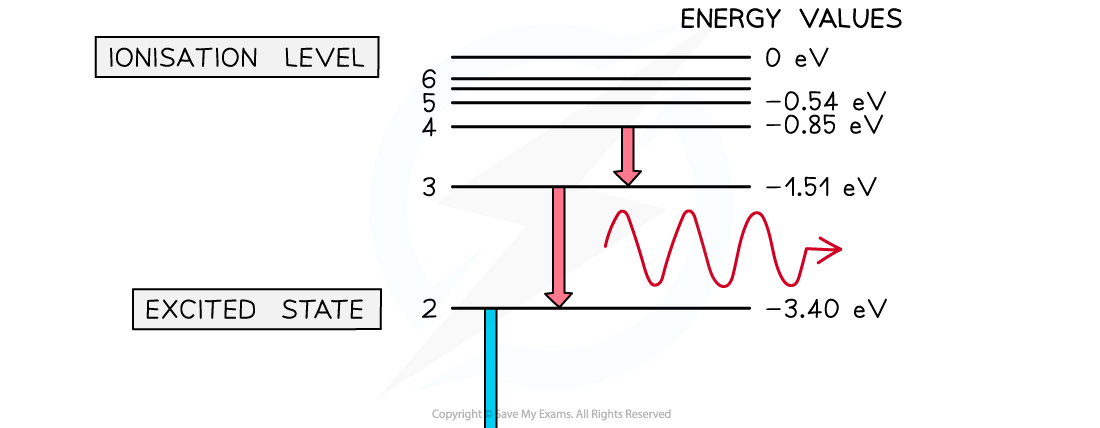

Electron energy levels in atomic hydrogen. Photons are emitted when an electron moves from a higher energy state to a lower energy state
Line Spectra
- Line spectra is a phenomenon which occurs when excited atoms emit light of certain wavelengths which correspond to different colours
- The emitted light can be observed as a series of coloured lines with dark spaces in between
- These series of coloured lines are called line or atomic spectra
- Each element produces a unique set of spectral lines
- No two elements emit the same set of spectral lines, therefore, elements can be identified by their line spectrum
- There are two types of line spectra: emission spectra and absorption spectra
Emission Spectra
- When an electron transitions from a higher energy level to a lower energy level, this results in the emission of a photon
- Each transition corresponds to a different wavelength of light and this corresponds to a line in the spectrum
- The resulting emission spectrum contains a set of discrete wavelengths, represented by coloured lines on a black background
- Each emitted photon has a wavelength which is associated with a discrete change in energy, according to the equation:
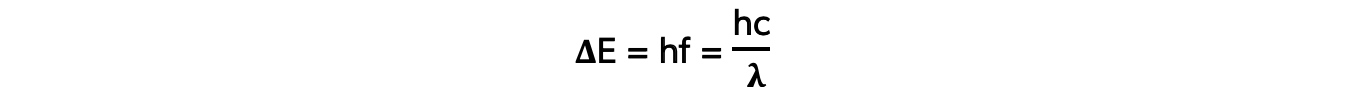
- Where:
- ΔE = change in energy level (J)
- h = Planck’s constant (J s)
- f = frequency of photon (Hz)
- c = the speed of light (m s-1)
- λ = wavelength of the photon (m)
- Therefore, this is evidence to show that electrons in atoms can only transition between discrete energy levels
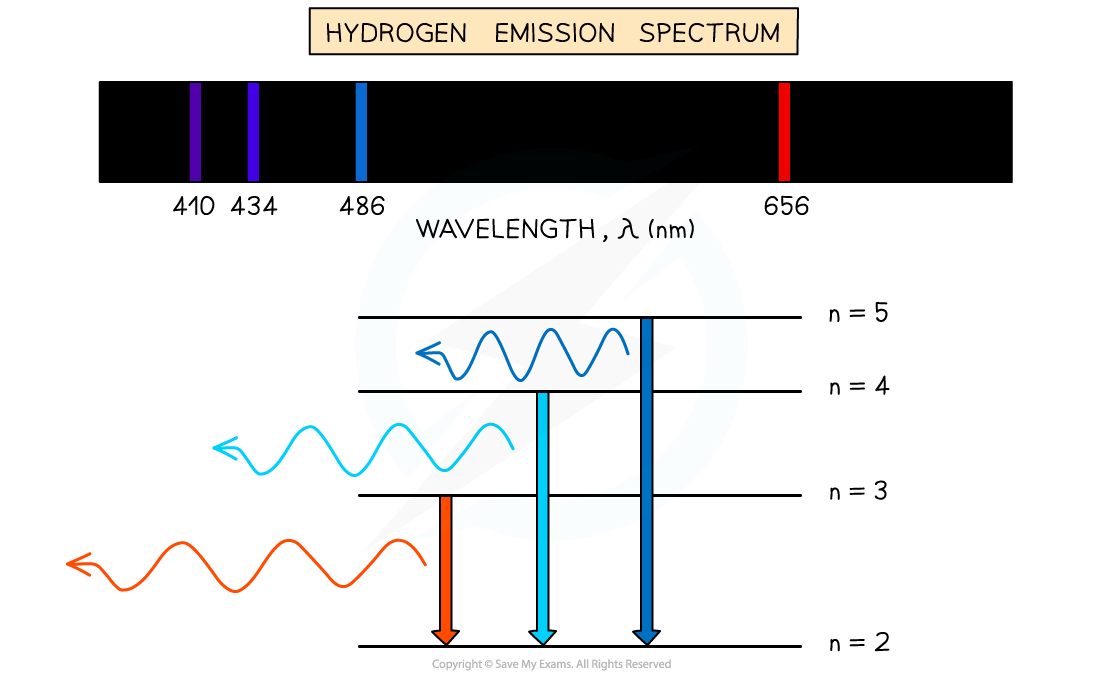
Emission spectrum of Hydrogen gas
Absorption Spectra
- An atom can be raised to an excited state by the absorption of a photon
- When white light passes through a cool, low pressure gas it is found that light of certain wavelengths are missing
- This type of spectrum is called an absorption spectrum
- An absorption spectrum consists of a continuous spectrum containing all the colours with dark lines at certain wavelengths
- These dark lines correspond exactly to the differences in energy levels in an atom
- When these electrons return to lower levels, the photons are emitted in all directions, rather than in the original direction of the white light
- Therefore, some wavelengths appear to be missing
- The wavelengths missing from an absorption spectrum are the same as their corresponding emission spectra of the same element
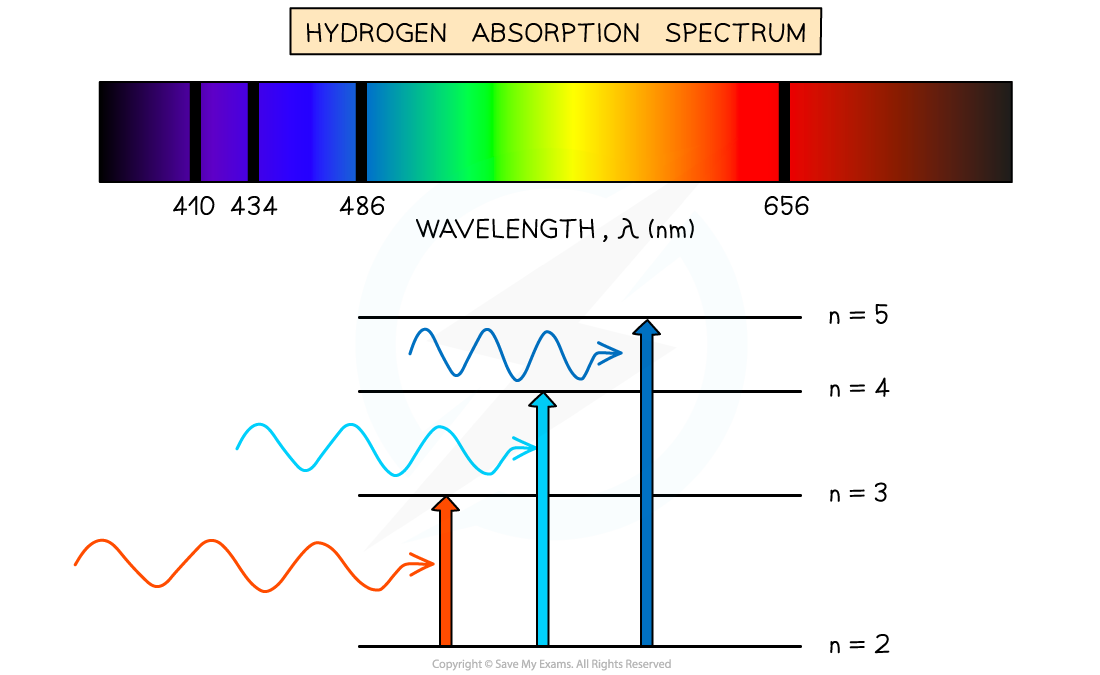
Absorption spectrum of Hydrogen gas
Difference in Discrete Energy Levels
- The difference between two energy levels is equal to a specific photon energy
- The energy (hf) of the photon is given by:
ΔE = hf = E2 - E1
- Where:
- E1 = Energy of the higher level (J)
- E2 = Energy of the lower level (J)
- h = Planck’s constant (J s)
- f = Frequency of photon (Hz)
- Using the wave equation, the wavelength of the emitted, or absorbed, radiation can be related to the energy difference by the equation:
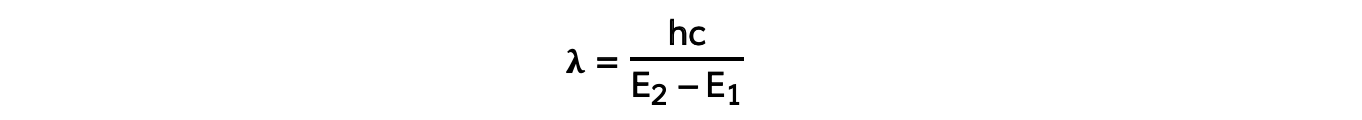
- This equation shows that the larger the difference in energy of two levels ΔE (E2 - E1) the shorter the wavelength λ and vice versa
Worked Example
Some electron energy levels in atomic hydrogen are shown below.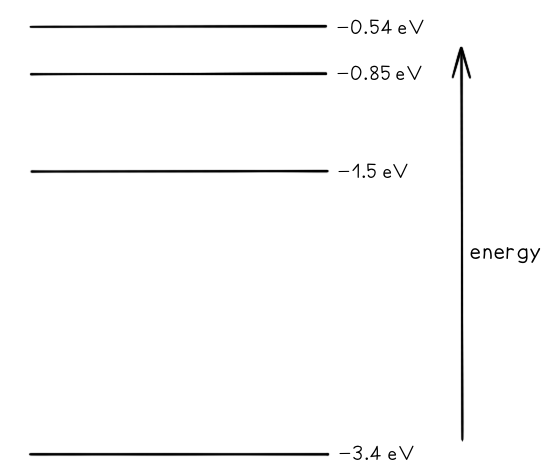 The longest wavelength produced as a result of electron transitions between two of the energy levels is 4.0 × 10–6 m.a) Draw and mark:
The longest wavelength produced as a result of electron transitions between two of the energy levels is 4.0 × 10–6 m.a) Draw and mark:
- The transition giving rise to the wavelength of 4.0 × 10–6 m with letter L.
- The transition giving rise to the shortest wavelength with letter S.
b) Calculate the wavelength for the transition giving rise to the shortest wavelength.
Part (a)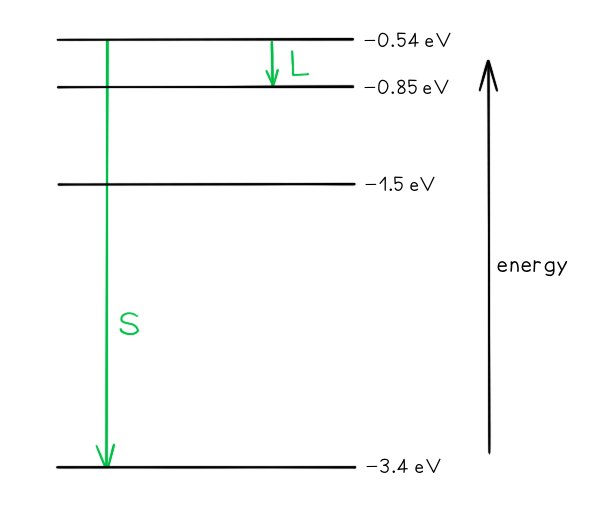
-
- Photon energy and wavelength are inversely proportional
- Therefore, the largest energy change corresponds to the shortest wavelength (line S)
- The smallest energy change corresponds to the longest wavelength (line L)
Part (b)
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





