- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
USACO 2020 US Open Contest, Silver Problem 3. The Moo Particle
USACO 2020 US Open Contest, Silver Problem 3. The Moo Particle
Quarantined for their protection during an outbreak of COWVID-19, Farmer John's cows have come up with a new way to alleviate their boredom: studying advanced physics! In fact, the cows have even managed to discover a new subatomic particle, which they have named the "moo particle".
The cows are currently running an experiment involving NN moo particles (1≤N≤1051≤N≤105). Particle ii has a "spin" described by two integers xixi and yiyi in the range −109…109−109…109 inclusive. Sometimes two moo particles interact. This can happen to particles with spins (xi,yi)(xi,yi) and (xj,yj)(xj,yj) only if xi≤xjxi≤xj and yi≤yjyi≤yj. Under these conditions, it's possible that exactly one of these two particles may disappear (and nothing happens to the other particle). At any given time, at most one interaction will occur.
The cows want to know the minimum number of moo particles that may be left after some arbitrary sequence of interactions.
INPUT FORMAT (file moop.in):
The first line contains a single integer NN, the initial number of moo particles. Each of the next NN lines contains two space-separated integers, indicating the spin of one particle. Each particle has a distinct spin.
OUTPUT FORMAT (file moop.out):
A single integer, the smallest number of moo particles that may remain after some arbitrary sequence of interactions.
SAMPLE INPUT:
4 1 0 0 1 -1 0 0 -1
SAMPLE OUTPUT:
1
One possible sequence of interactions:
- Particles 1 and 4 interact, particle 1 disappears.
- Particles 2 and 4 interact, particle 4 disappears.
- Particles 2 and 3 interact, particle 3 disappears.
Only particle 2 remains.
SAMPLE INPUT:
3 0 0 1 1 -1 3
SAMPLE OUTPUT:
2
Particle 3 cannot interact with either of the other two particles, so it must remain. At least one of particles 1 and 2 must also remain.
SCORING:
- Test cases 3-6 satisfy N≤1000.N≤1000.
- Test cases 7-12 satisfy no additional constraints.
Problem credits: Dhruv Rohatgi
USACO 2020 US Open Contest, Silver Problem 3. The Moo Particle 题解(翰林国际教育提供,仅供参考)
[/hide]
(Analysis by Benjamin Qi)
Construct an undirected graph where each vertex represents a moo particle and there exists an edge between two moo particles if they can interact. An interaction corresponds to removing a vertex with at least one adjacent edge.
Within each connected component, at least one particle must remain. Conversely, we can show that this is always attainable. Consider a spanning forest of the graph; just keep removing a particle that is a leaf in this forest.
It remains to show how to compute the number of connected components in faster than O(N2)O(N2). Sort the moo particles in increasing order of xx and then yy. Initially, suppose that each particle is its own connected component. Then while there exist two connected components that are adjacent in the order such that the minimum yy-coordinate in the left component is at most the maximum yy-coordinate of the right coordinate, combine them together.
For the following input (a combination of the two samples), the answer is 3.
7 1 0 0 1 -1 0 0 -1 3 -5 4 -4 2 -2
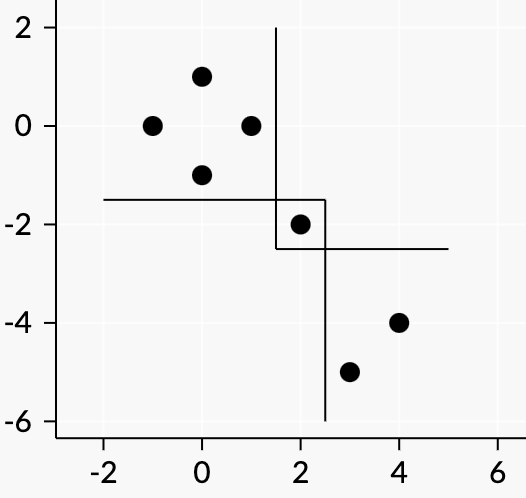
After this is done, the ii-th moo particle in the sorted order is not in the same connected component as the i+1i+1-st if and only if min(y1,y2,…,yi)>max(yi+1,yi+2,…,yN)min(y1,y2,…,yi)>max(yi+1,yi+2,…,yN) (which automatically implies that max(x1,x2,…,xi)<min(xi+1,xi+2,…,xN)max(x1,x2,…,xi)<min(xi+1,xi+2,…,xN)). So after sorting we only need O(N)O(N) additional time to compute the answer.
Dhruv Rohatgi's code:
#include <iostream>
#include <algorithm>
using namespace std;
#define MAXN 100000
int N;
int x[MAXN], y[MAXN];
int cid[MAXN];
int minl[MAXN];
int maxr[MAXN];
bool cmp(int a,int b)
{
if(x[a]==x[b]) return y[a]<y[b];
return x[a]<x[b];
}
int main()
{
freopen("moop.in","r",stdin);
freopen("moop.out","w",stdout);
cin >> N;
for(int i=0;i<N;i++)
{
cin >> x[i] >> y[i];
cid[i] = i;
}
sort(cid,cid+N,cmp);
minl[0] = y[cid[0]];
for(int i=1;i<N;i++)
minl[i] = min(minl[i-1], y[cid[i]]);
maxr[N-1] = y[cid[N-1]];
for(int i=N-2;i>=0;i--)
maxr[i] = max(maxr[i+1], y[cid[i]]);
int ans = 1;
for(int i=0;i<N-1;i++)
if(minl[i] > maxr[i+1])
ans++;
cout << ans << 'n';
}
Related (but harder) problems:
[/hide]
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





