How do we find averages if there are lots of values?

• In reality there will be far more data to work with than just a few numbers
• In these cases the data is usually organised in such a way to make it easier to follow and understand – for example in a table or chart
• We can still find the mean, median and mode but have to ensure we understand what the table or chart is telling us

 

What do I need to know?

• Finding the median and mode from tables/charts is fairly straightforward once you understand what the table/chart is telling you so these notes focus mainly on finding the mean

 

 

1. Finding the mean from (discrete) data presented in tables

• Tables allow data to be summarised neatly – and quite importantly it puts it into order

 

Eg. the number of pets owned by 40 pupils in year 11 are summarised in the table below:

 

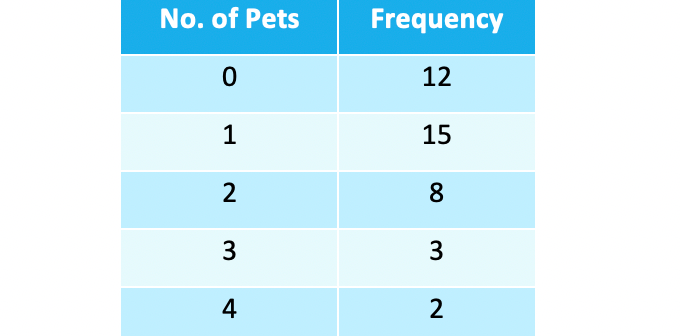
Work out the mean and median number of pets per pupil.

 

The mean can be found as you long as understand what the table is telling you:

 

It tells you:

12 (of the 40) pupils had no pets; 15 of them had 1 pet; 8 had 2 pets

 

This means you can add up all the 0’s very quickly, all the 1’s very quickly etc. using multiplication:  12 x 0 = 0, 15 x 1 = 15, etc.

 

 

The easiest way to do this is to add another column to the table and adding a total row will prove useful in the next stage too:

 

 

 

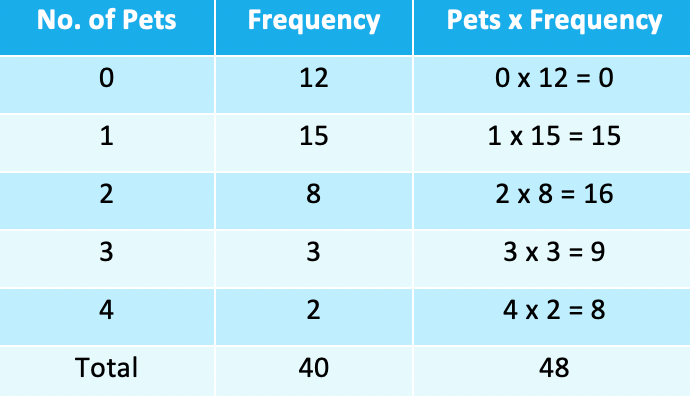
• You can now see that the total number of pets for the whole of the 40 pupils is 48
• If you hadn’t been told in the question, the total of the frequency column would’ve told you how many pupils there are
• You can now find the mean:

 

48 ÷ 40 = 1.2

 

The mean number of pets is 1.2 (pets per pupil)

• You may sometimes see the number of pets called x and the frequency f so the last column would be:f x  (f times x)

 

 

2. Median

• The median is a little complicated to understand but easy to work out
• Remember you are looking for the middle value when the data is in order
• For the example above the table is in order (0, then 1, 2, etc.) – so you need to work out which of the 40 values is in the median position
• To do this you add one to the number of values and divide by 2

 

(40 + 1) ÷ 2 = 20.5 – so the median is in the “20.5^th” position

 

• The table tells you the first twelve numbers on the list are all 0’s, the next 15 are all 1’s – so the “20.5^th” value in the list must be a 1The median number of pets is 1(Note that the “20.5^th” value is referring to halfway between the 20^th and 21^st values. Both of these are 1’s so median must be 1 (or use (1 + 1) ÷ 2 = 1 if you’re not convinced!)

 

 

3. Mode (modal value)

• The mode (or modal value) is simple to identify
• Look for the highest frequency – and then you find the corresponding data value

 

In the example above the highest frequency is 15

 

Modal number of pets = 1

• Don’t confuse the number of pets with the frequency

 

Worked Example

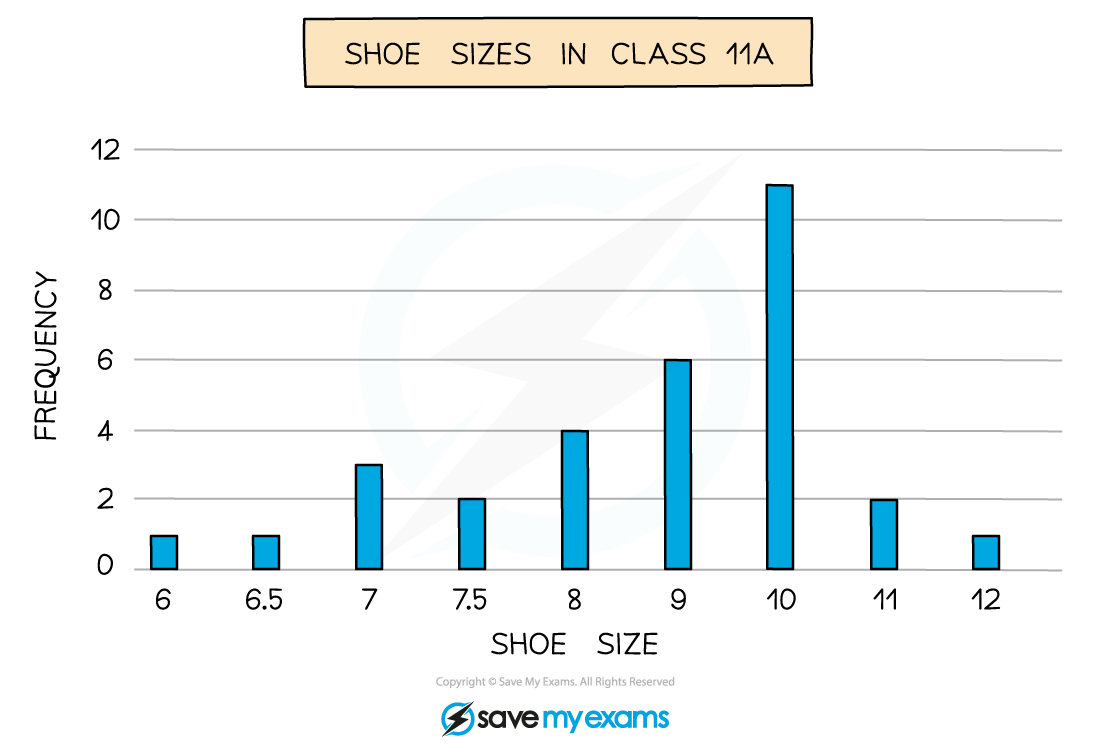
Worked Example

Worked Example