- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel IGCSE Maths 复习笔记 4.10.2 Sine & Cosine Rules, Area of Triangle - Harder
Edexcel IGCSE Maths 复习笔记 4.10.2 Sine & Cosine Rules, Area of Triangle - Harder
Choosing which rule or formula to use
- It is important to be able to decide which Rule or Formula to use to answer a question
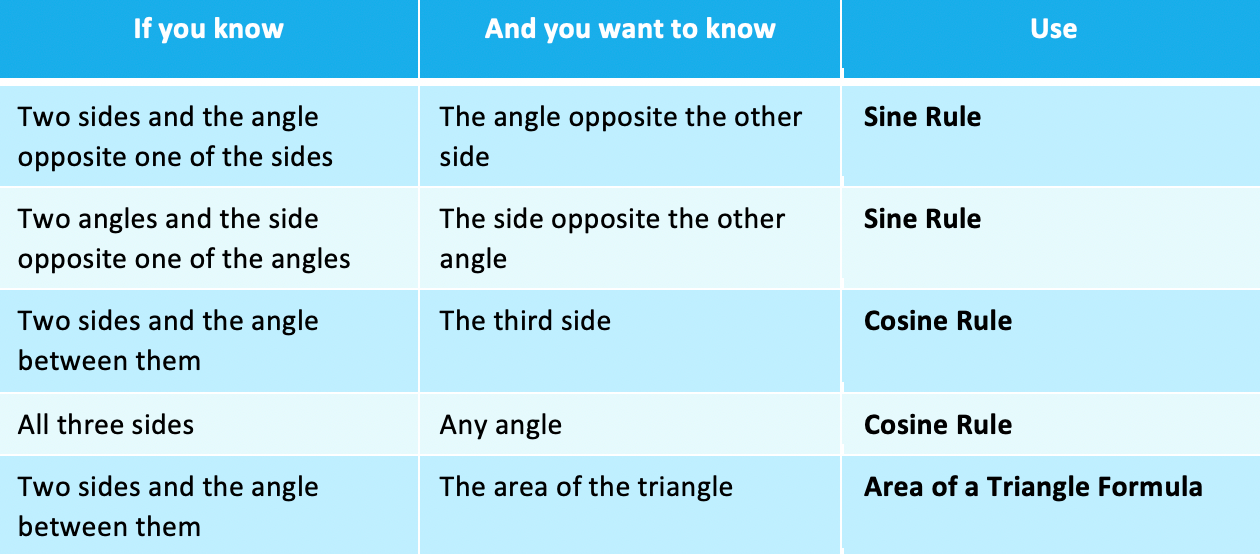
- This table summarises the possibilities:
Using the cosine rules to find angles

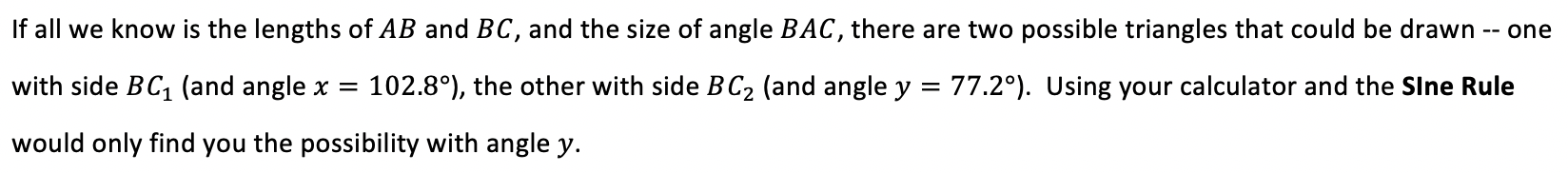
Exam Tip
In more involved exam questions, you may have to use both the Cosine Rule and the Sine Rule over several steps to find the final answer.If your calculator gives you a ‘Maths ERROR’ message when trying to find an angle using the Cosine Rule, you probably subtracted things the wrong way around when you rearranged the formula.The Sine Rule can also be written ‘flipped over’: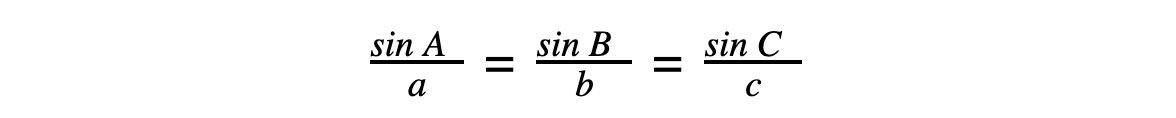 This is more useful when we are using the rule to find anglesWhen finding angles with the Sine Rule, use the info in the question to decide whether you have the acute angle case (ie the calculator value) or the obtuse angle case (ie, minus the calculator value).The Cosine Rule will never give you an ambiguous answer for an angle – as long as you put the right things into the calculator, the answer that comes out will be the correct angle
This is more useful when we are using the rule to find anglesWhen finding angles with the Sine Rule, use the info in the question to decide whether you have the acute angle case (ie the calculator value) or the obtuse angle case (ie, minus the calculator value).The Cosine Rule will never give you an ambiguous answer for an angle – as long as you put the right things into the calculator, the answer that comes out will be the correct angle
Worked Example
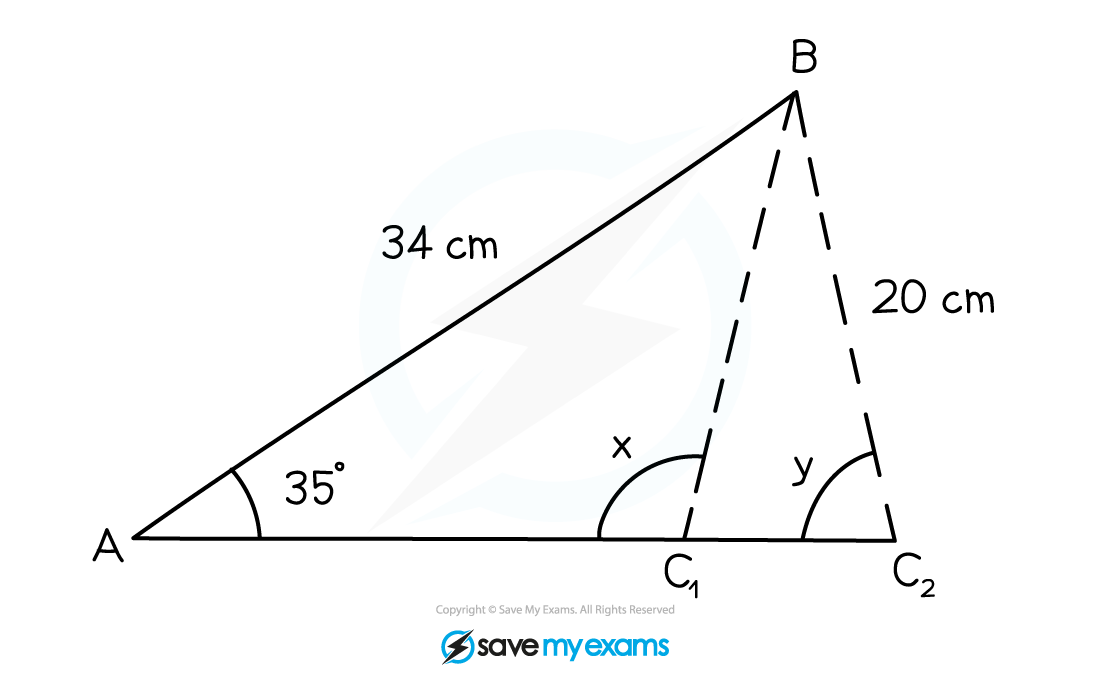
In the following triangle: a) Find the size of angle ABC.
a) Find the size of angle ABC.
b) Given that angle ACB is obtuse, use the Sine Rule and your answer from (a) to find the size of angle ABC.
Give your answers accurate to 1 d.p.
Worked Example

转载自savemyexam
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





