- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel IGCSE Maths 复习笔记 4.10.1 Sine & Cosine Rules, Area of a Triangle - Basics
Edexcel IGCSE Maths 复习笔记 4.10.1 Sine & Cosine Rules, Area of a Triangle - Basics
What are the sine & cosine rules, & the area of a triangle formula?
- Remember, Pythagoras and SOHCAHTOA only work in right-angled triangles
- The Sine Rule, Cosine Rule, and Area of a Triangle Formula allow us to answer triangle questions for ANY triangle
The sine rule, cosine rule, & area of a triangle formula
- In discussing these formulas, we usually label our triangle like this:
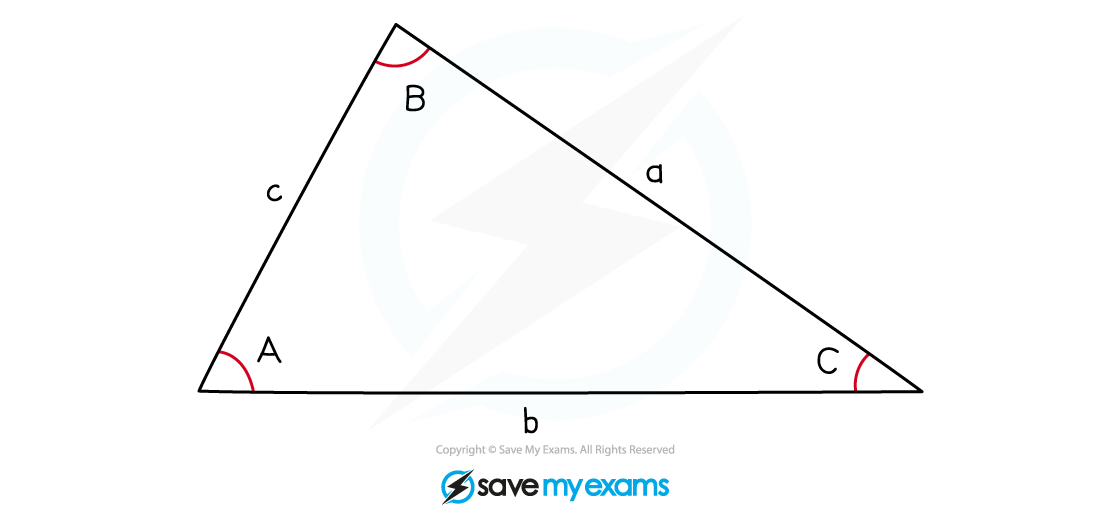
- Note: lowercase letters for side lengths, capital letters for angles — and make sure an angle and the side opposite it have the same letter
- The Sine Rule tells us that:
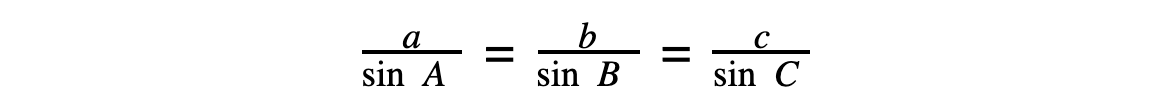
sin 90° =1 – so if one of the angles is 90°, this becomes ‘SOH’ from SOHCAHTOA
- The Cosine Rule tells us that:
a2 = b2 + c2 – 2bc cos A
cos 90° = 0 so if A = 90°, this becomes Pythagoras’ Theorem
- The Area of a Triangle Formula tells us that:sin 90° =1 so if C=90°, this becomes Area = ½ × base × height
Area = ½ ab sin C
- The Sine Rule can also be written ‘flipped over’:
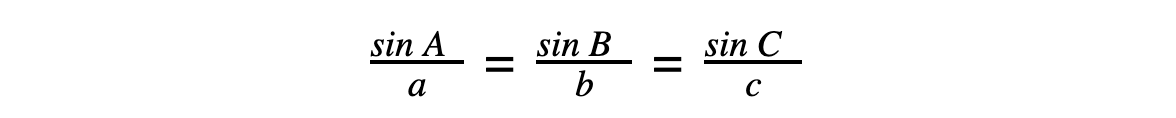
- This is more useful when we are using the rule to find angles
- These two versions of the Cosine Rule are also valid for the triangle above:
b2 = a2 + c2 - 2ac cos B
c2 = a2 + b2 - 2ab cos C
Note that it’s always the angle between the two sides in the final term
- These two versions of the Area of a Triangle Formula are also valid for the triangle above:
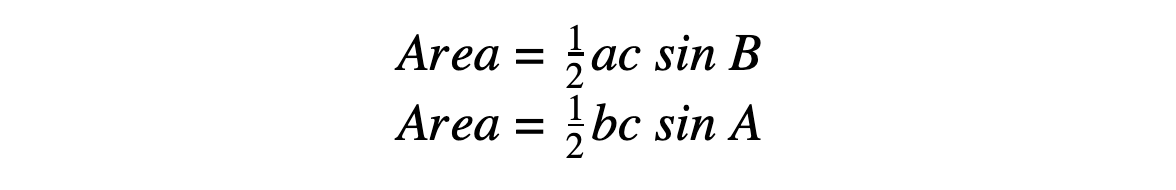
Note that it’s always the angle between the two sides on the right-hand side –you can always just relabel the sides and angles of your triangle, though, instead of worrying about alternate versions of the last two formulas
Worked Example
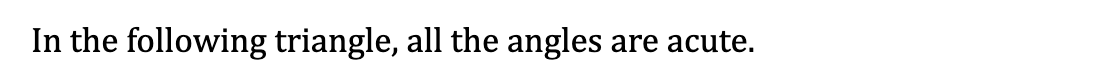

Worked Example

转载自savemyexam
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





