- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel IGCSE Maths 复习笔记 4.9.2 3D Pythagoras & SOHCAHTOA
Edexcel IGCSE Maths 复习笔记 4.9.2 3D Pythagoras & SOHCAHTOA
What are Pythagoras & SOHCAHTOA?
- Pythagoras’ Theorem helps us find missing side lengths of a right-angled triangle
- It is also frequently used for finding the distance (or length) of a line
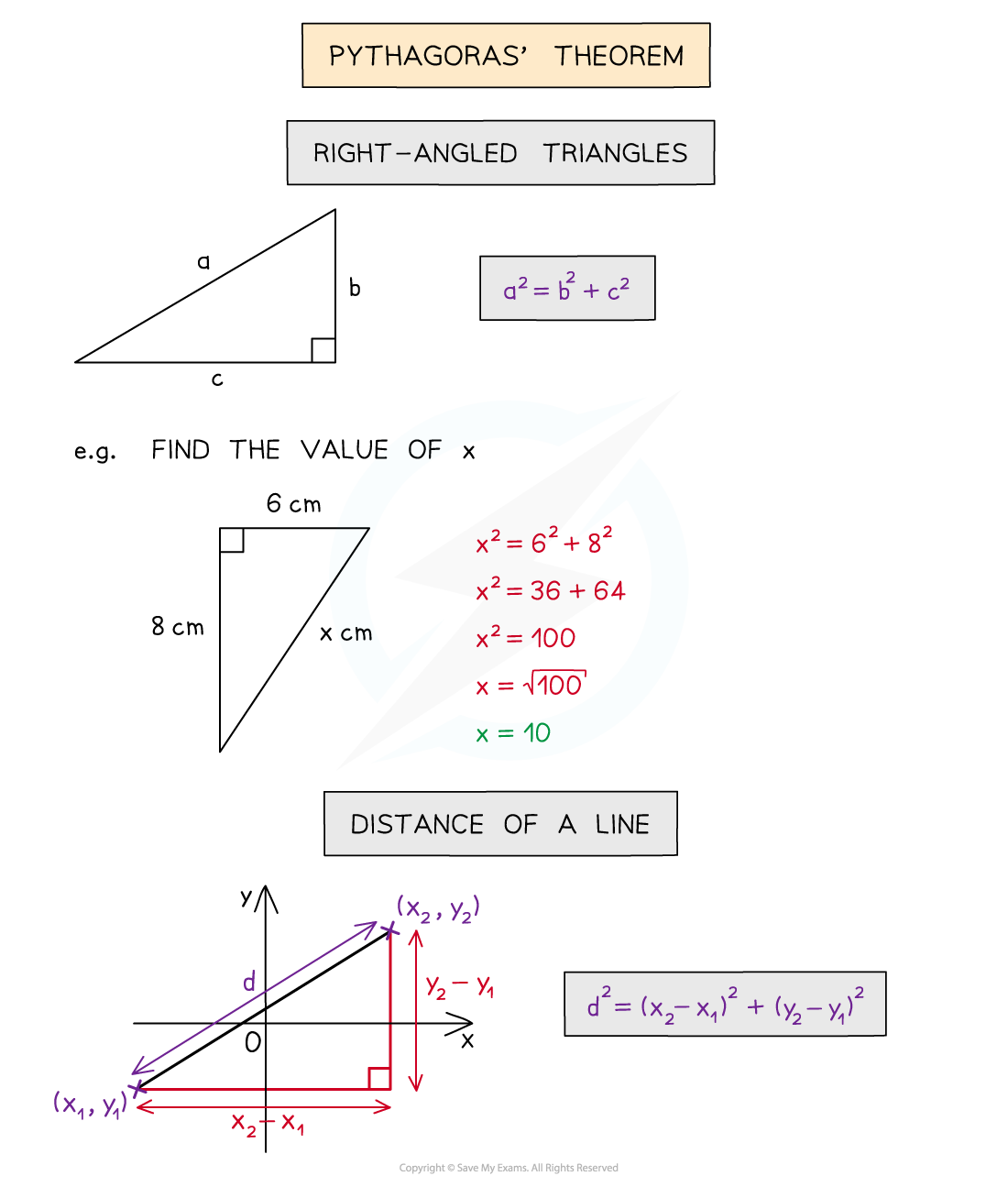
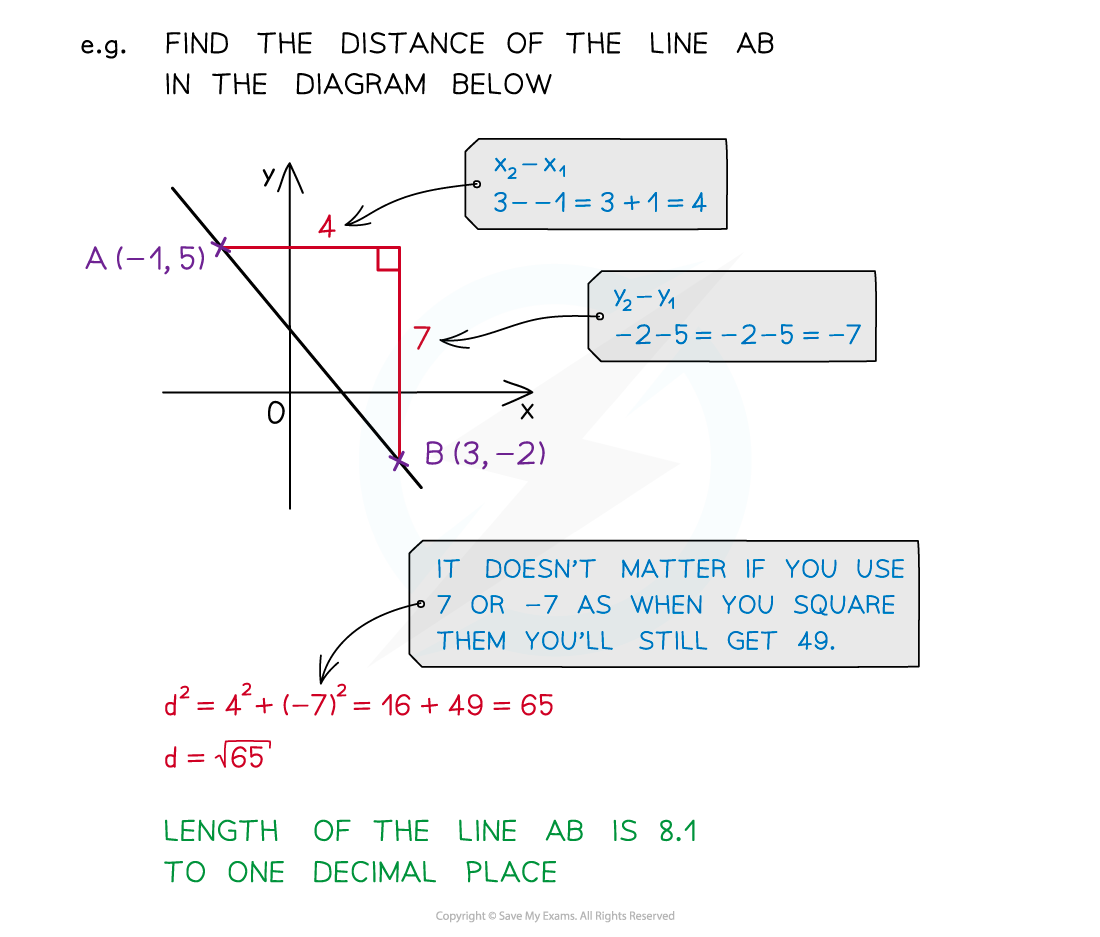
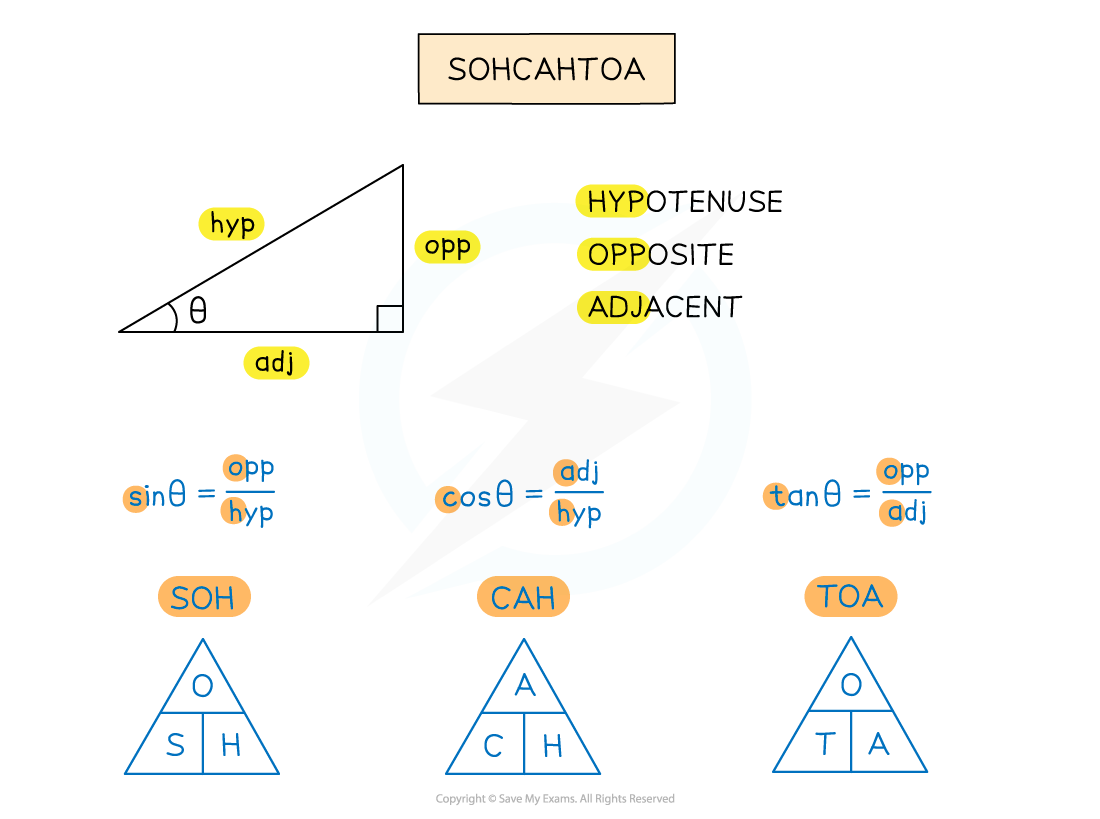
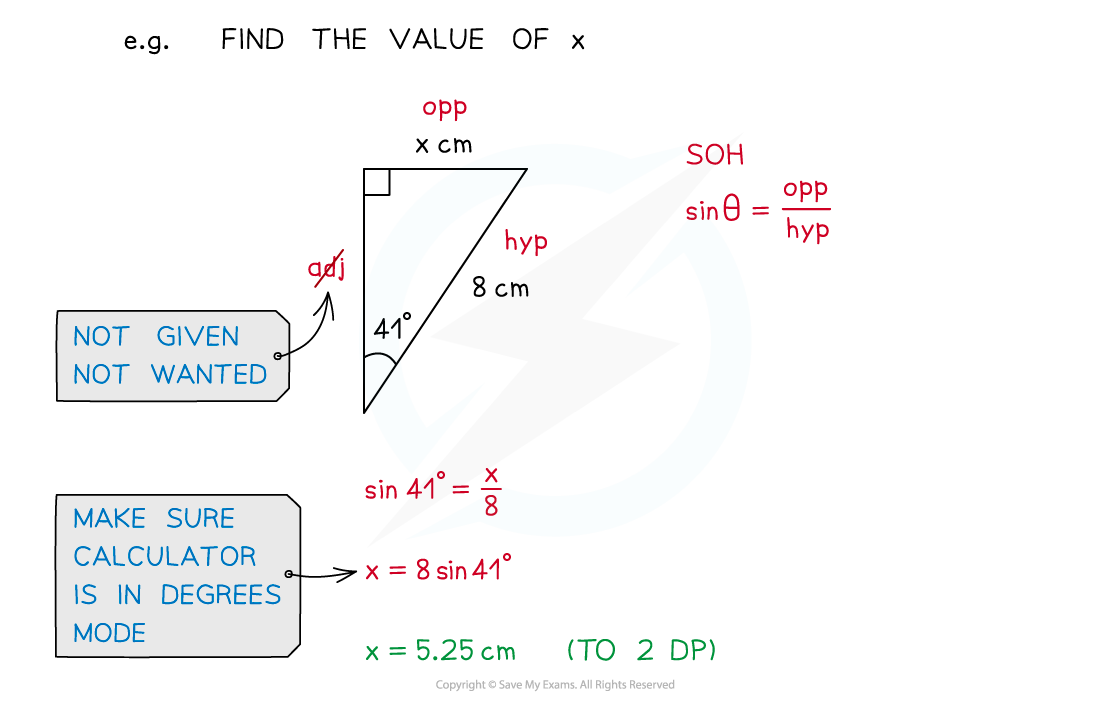
- SOHCAHTOA is an acronym for the three trigonometric ratios that connect angles (θ) and sides (Opposite, Hypotenuse and Adjacent) in a right-angled triangle
- Sine – SOH – sin θ = O ÷ H
- Cosine – CAH – cos θ = A ÷ H
- Tangent – TOA – tan θ = O ÷ A
How does Pythagoras work in 3D?
- 3D shapes can often be broken down into several 2D shapes
- For example nets and surface area
- With Pythagoras’ Theorem problems you will be specifically looking for right‑angled triangles
- The right-angled triangles you need will have two known sides and one unknown side
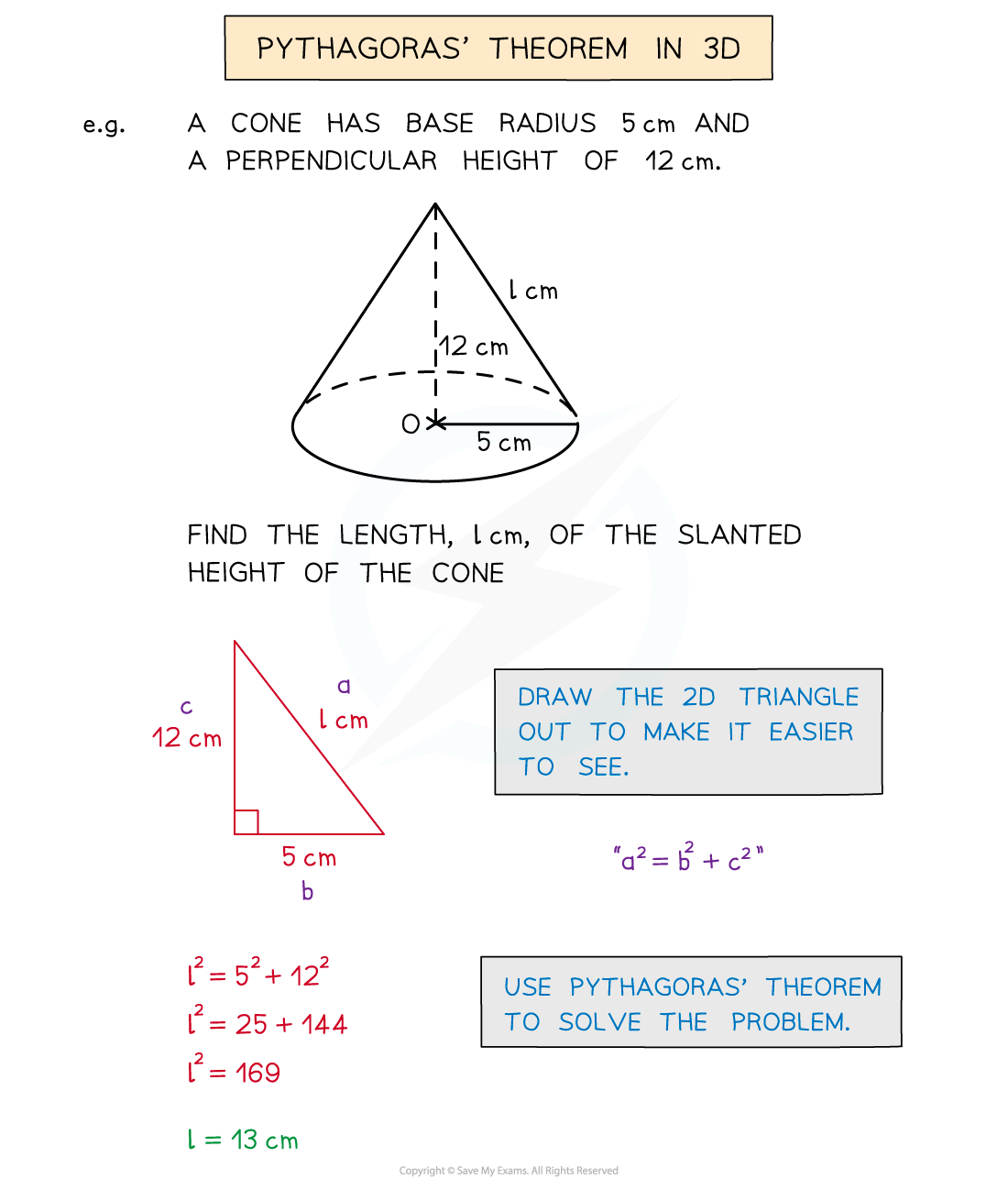
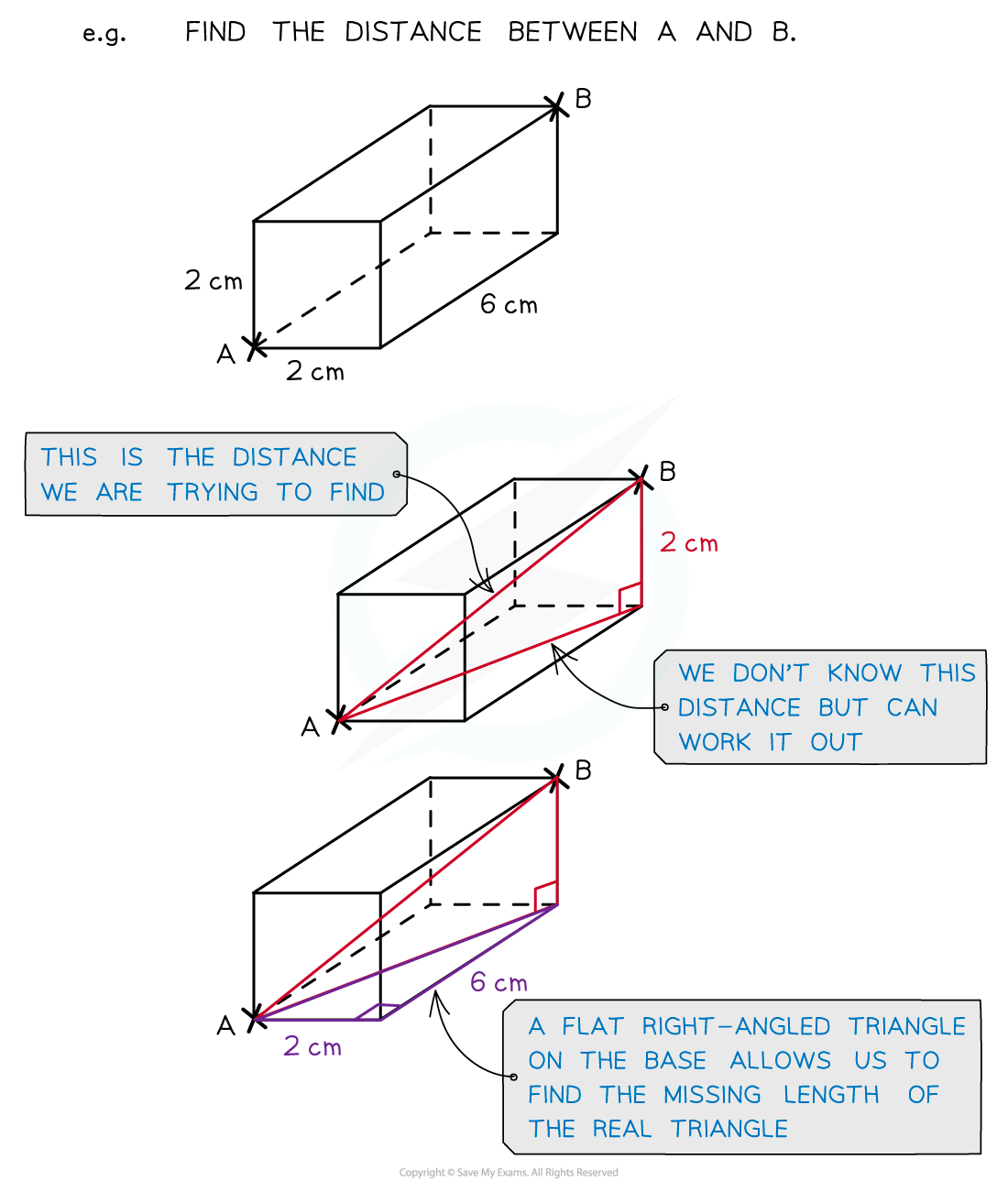
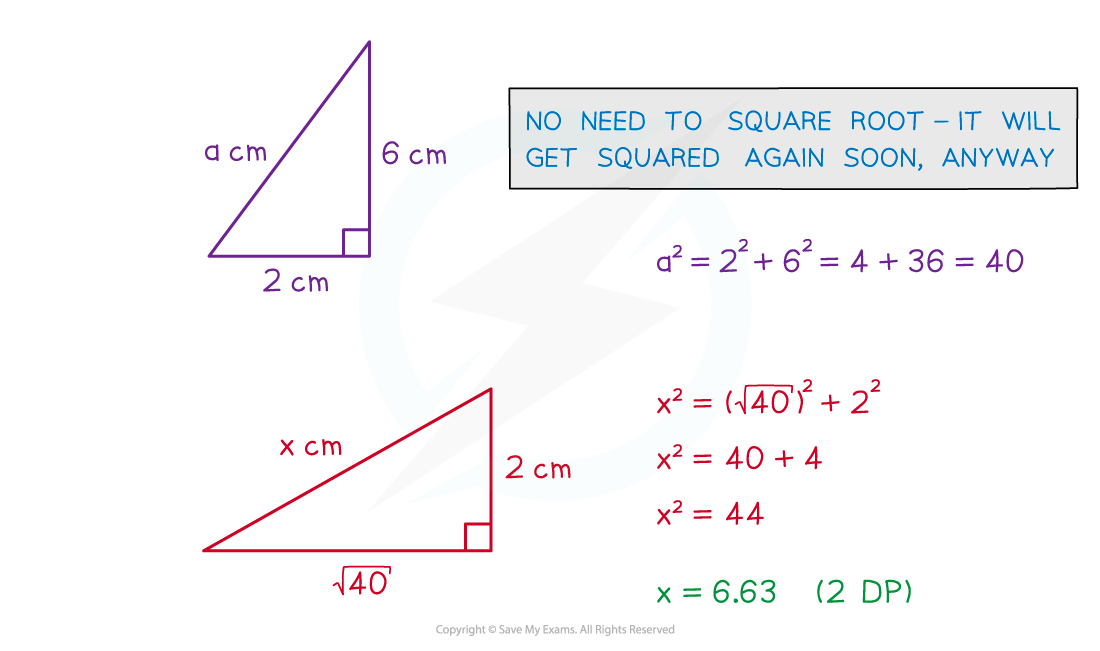
- There is a 3D version of the Pythagoras’ Theorem formula
- d2 = x2 + y2 + z2
- However it is usually far easier to see a problem by splitting it into two or more 2D problems

How does SOHCAHTOA work in 3D?
- Again look for a combination of right-angled triangles that would lead to the missing angle or side
- The angle you are working with can be awkward in 3D
- The angle between a line and a plane is not obvious
- If unsure, put a point on the line and draw a new line to the planeThis should create a right-angled triangle
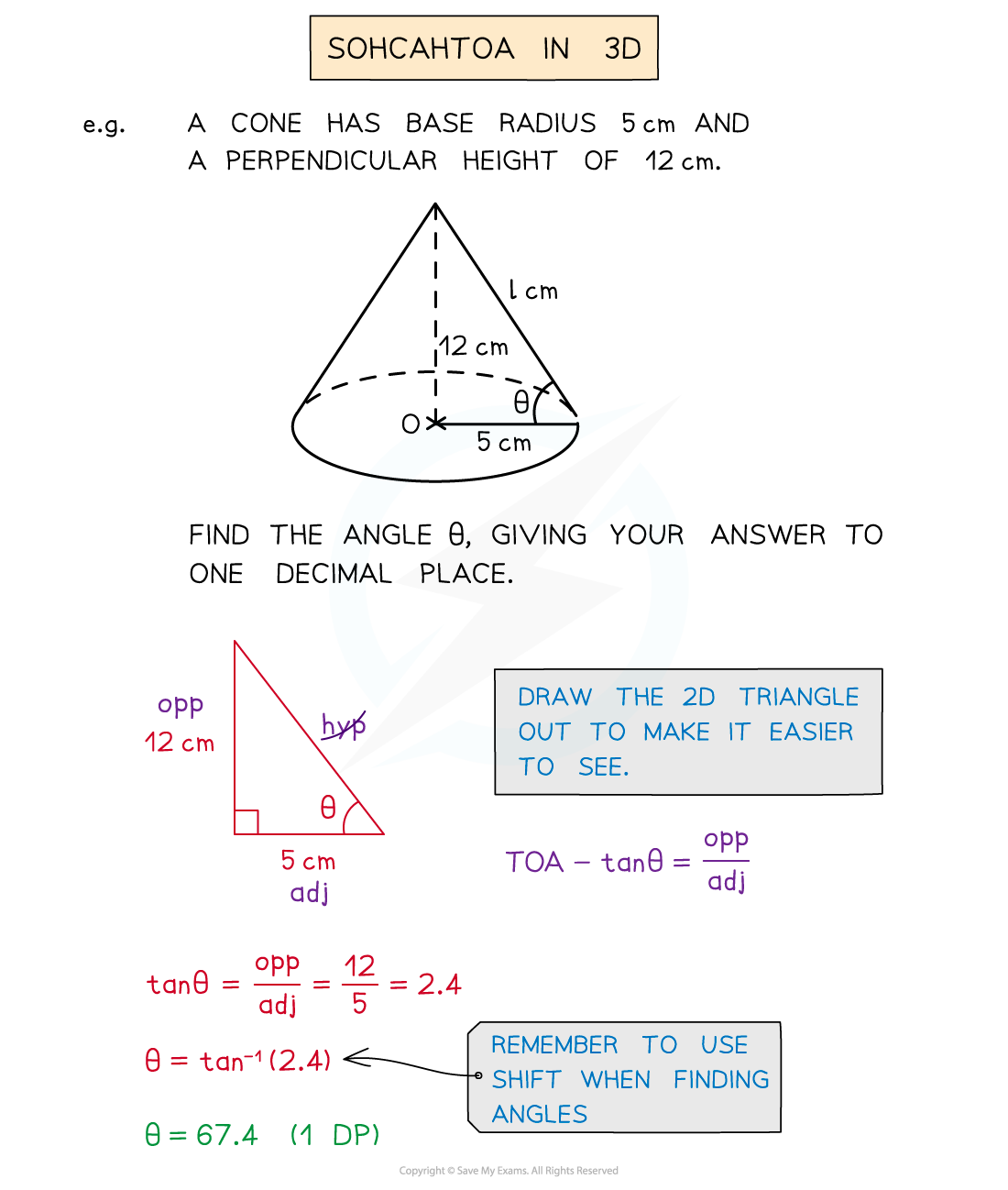
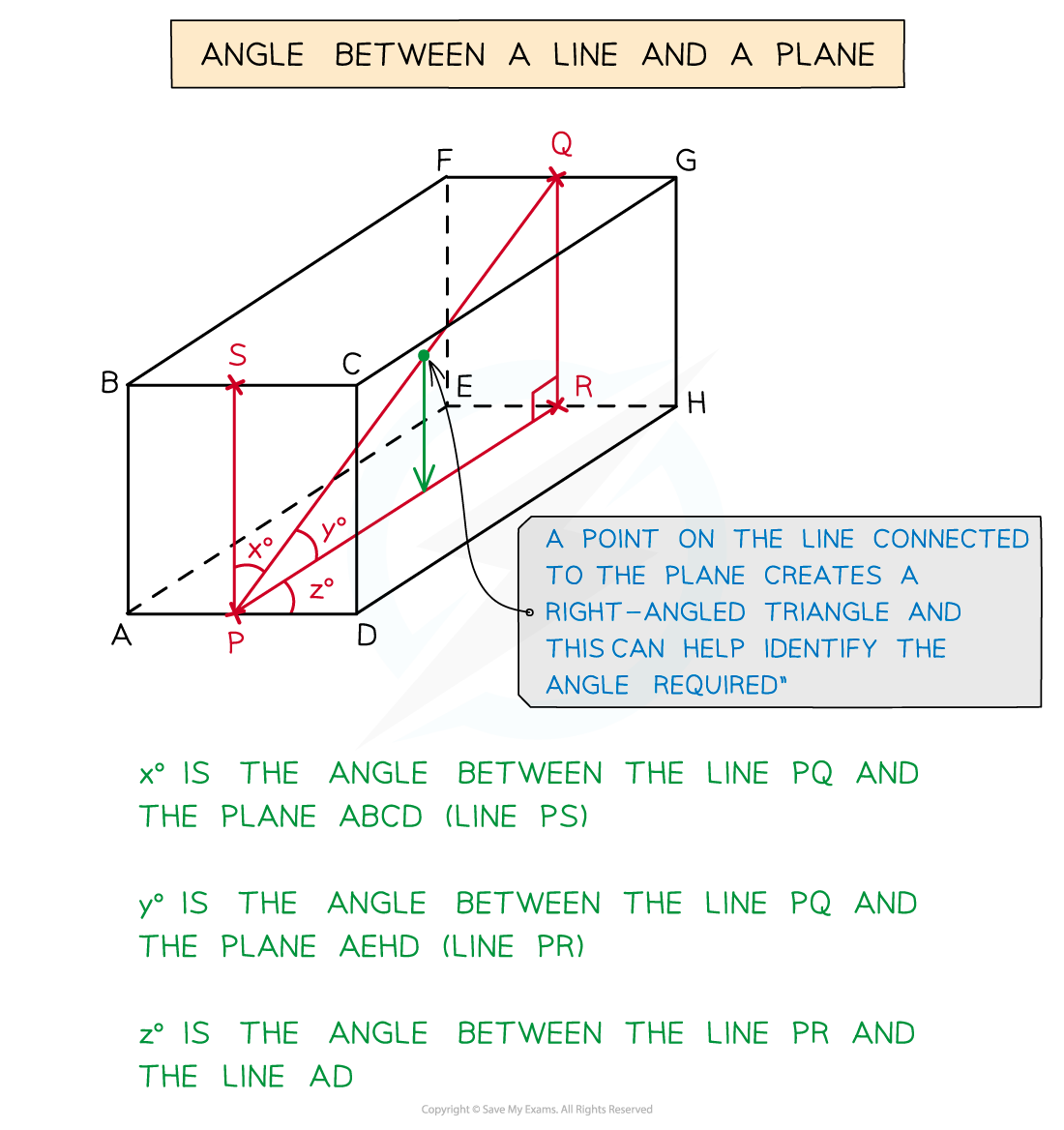
- Once you have your 2D triangle(s) you can begin to solve problems

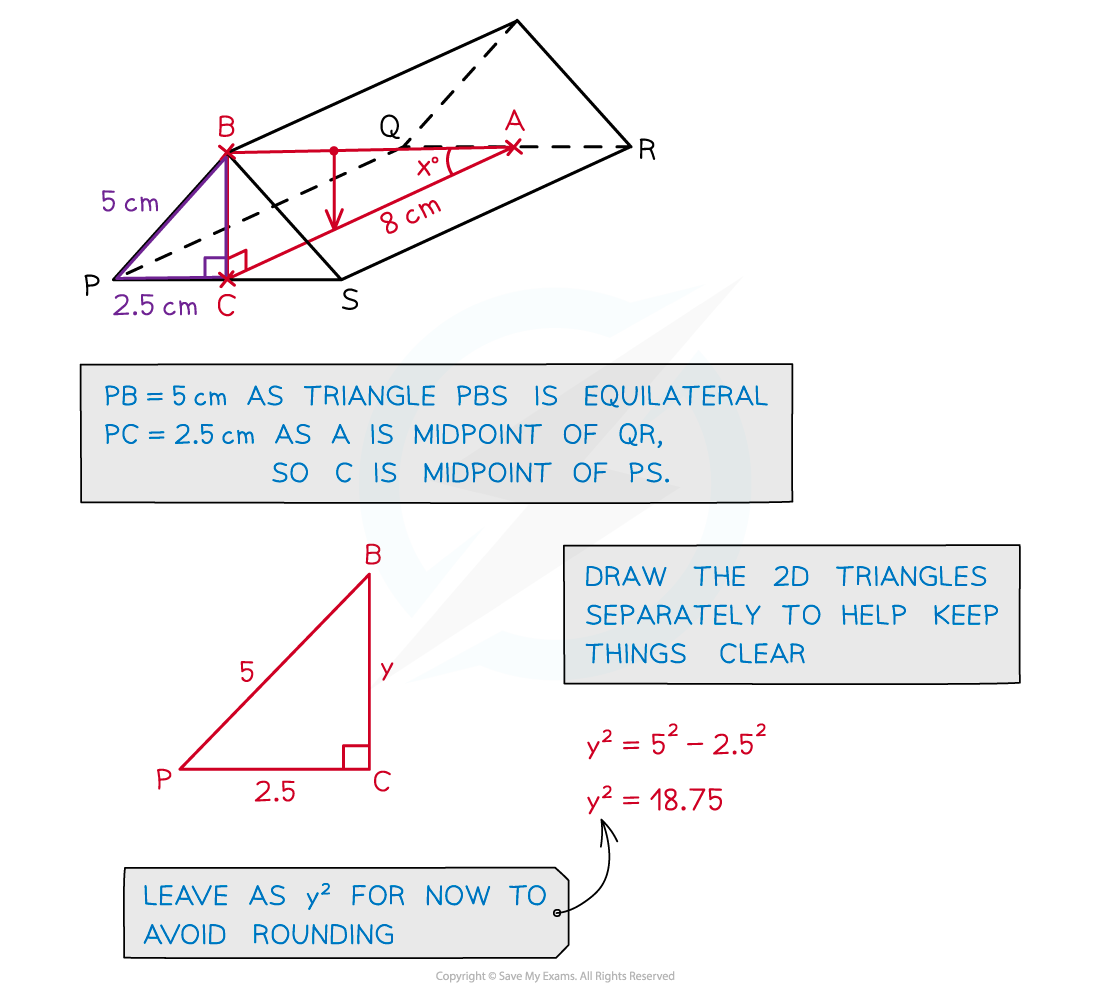
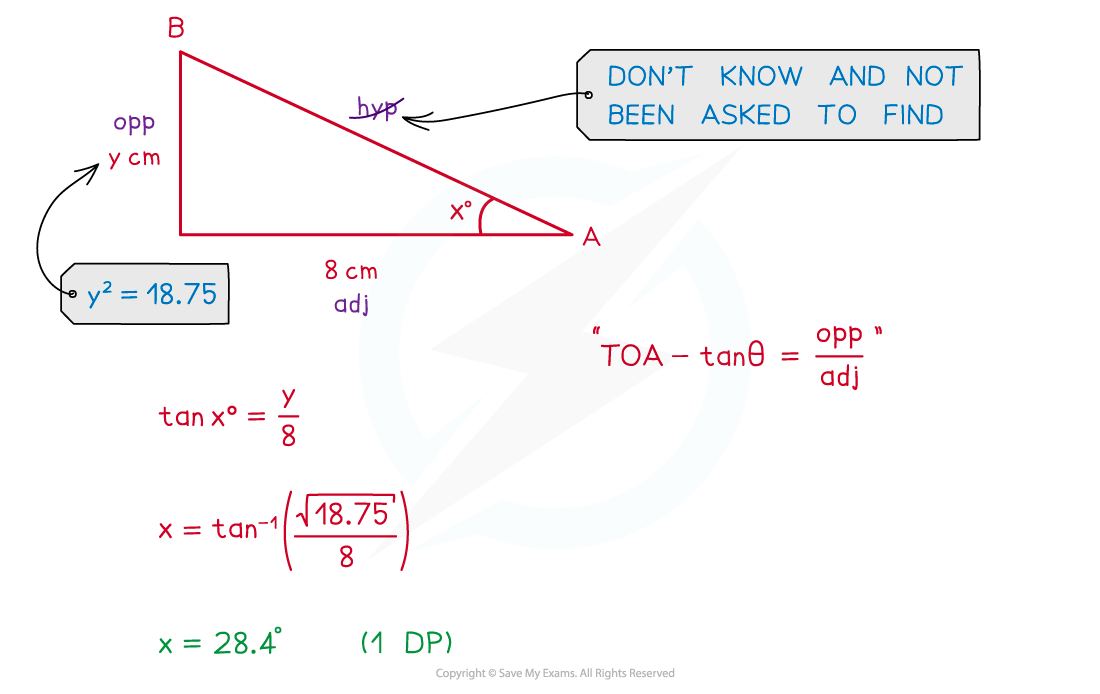
Exam Tip
Add lines/triangles/etc. to any given diagram to help you see the problem and draw any 2D triangles separately as a 3D diagram can get hard to follow.
Worked Example

Worked Example
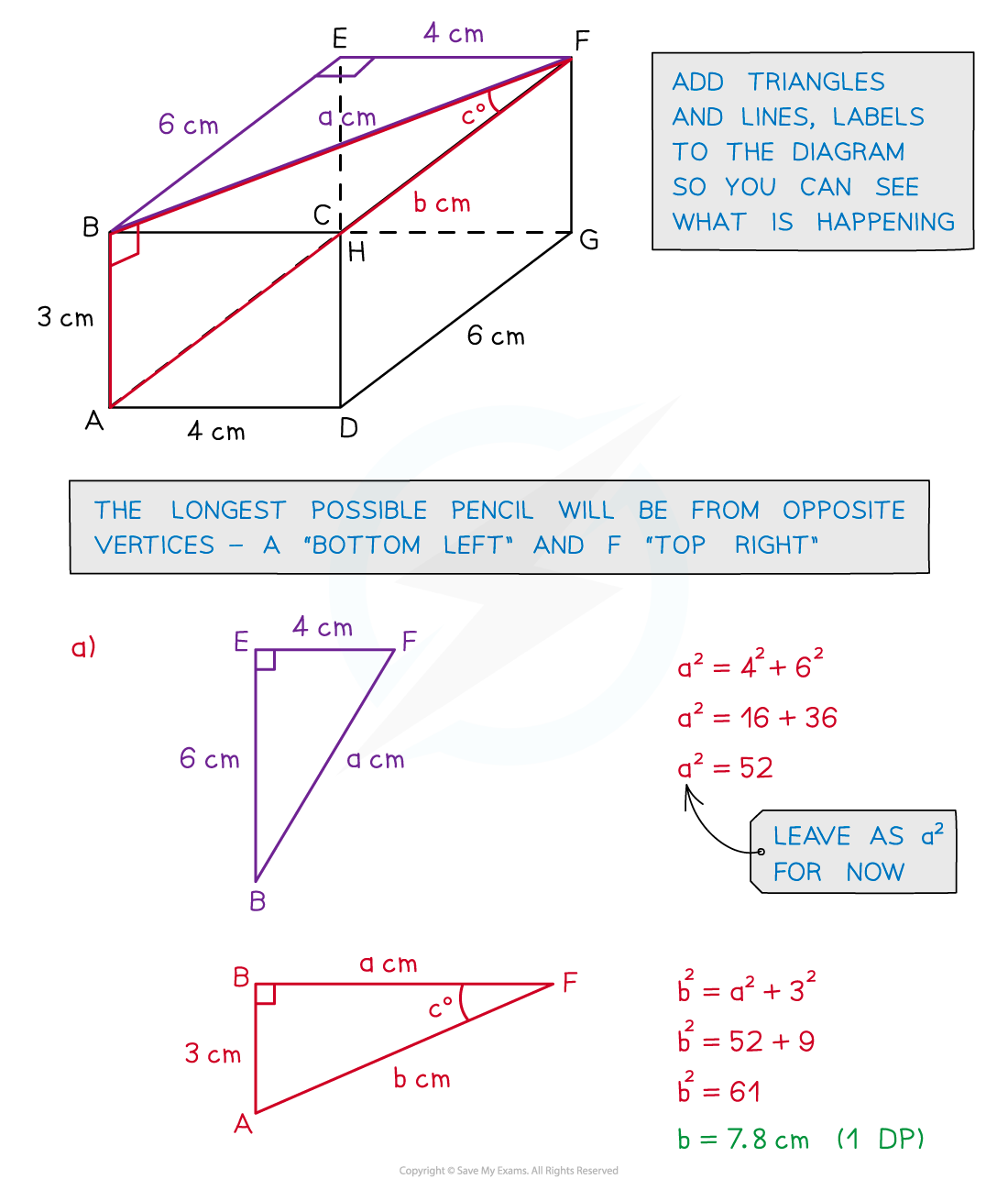
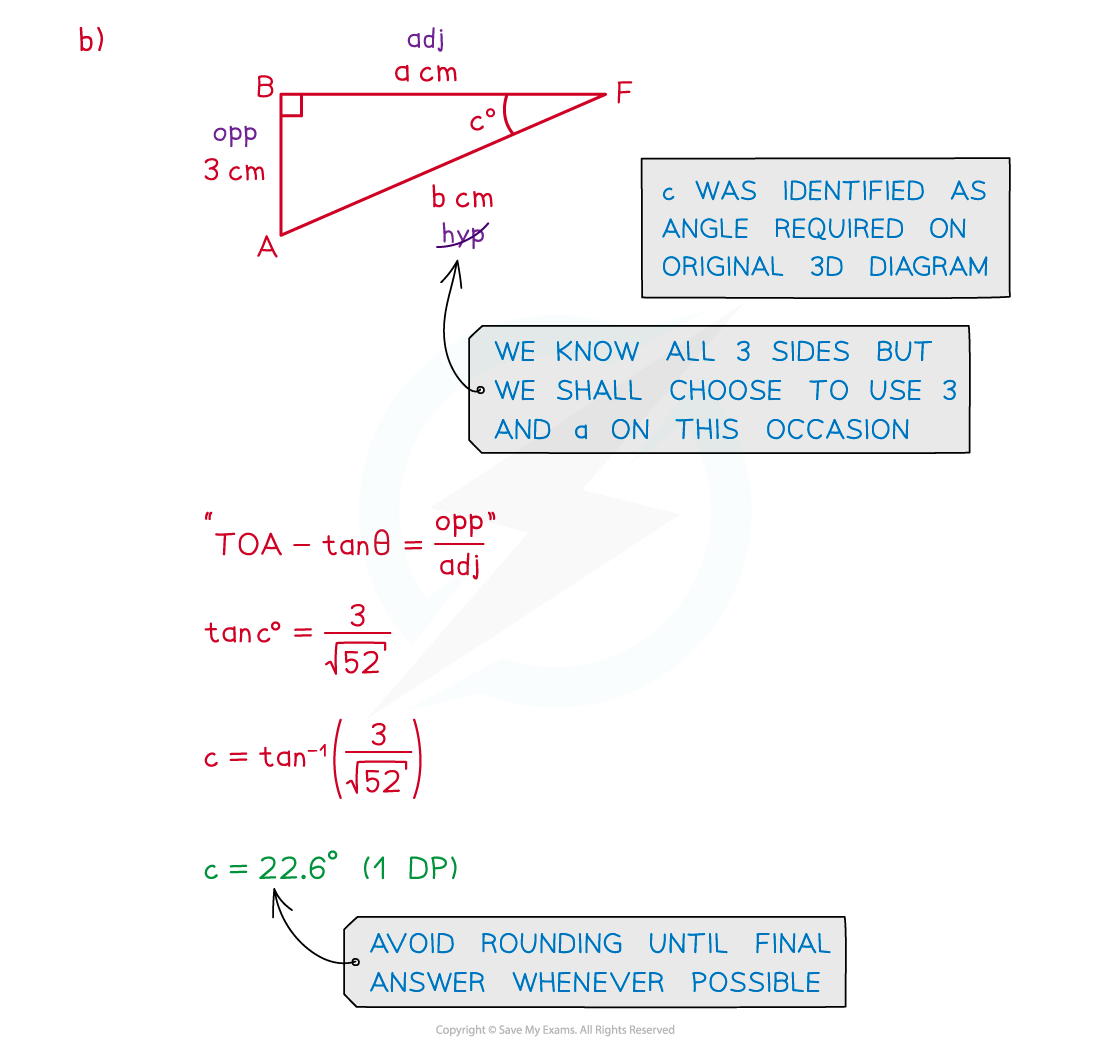
转载自savemyexam
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





