- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel IGCSE Maths 复习笔记 3.11.2 Differentiation - Turning Points
Edexcel IGCSE Maths 复习笔记 3.11.2 Differentiation - Turning Points
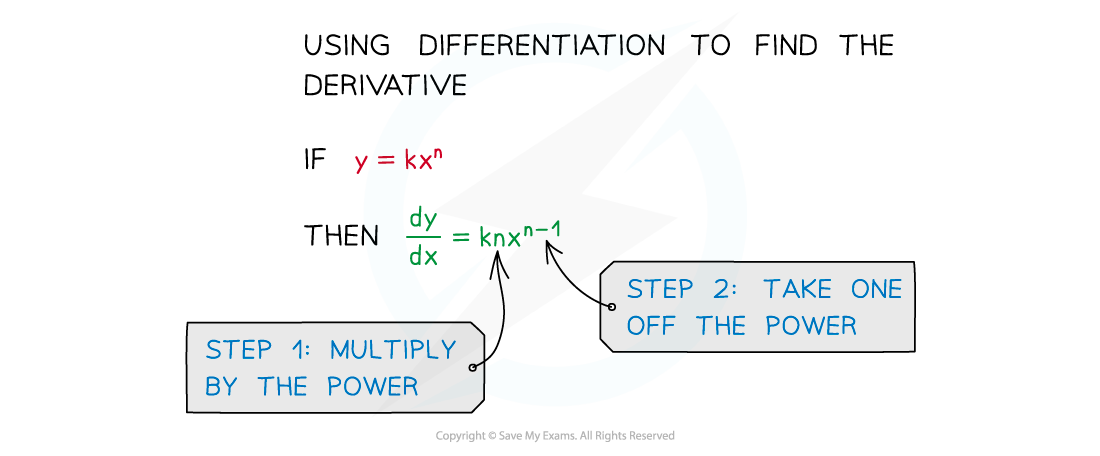
Remind me of the rule for differentiating powers
- If y = kxn then dy/dx = knxn-1
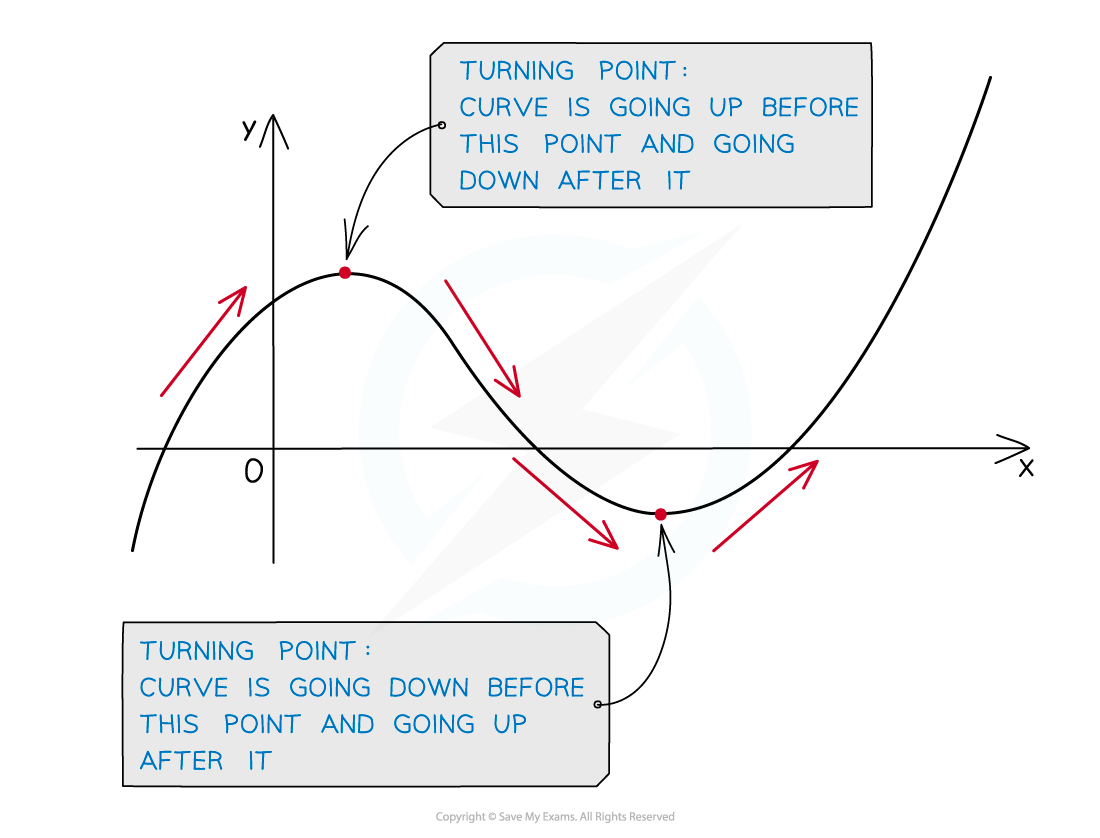
What is a turning point?
- The easiest way to think of a turning point is that it is a point at which a curve changes from moving upwards to moving downwards, or vice versa
- Turning points are also called stationary points
- Ensure you are familiar with Differentiation – Basics before moving on
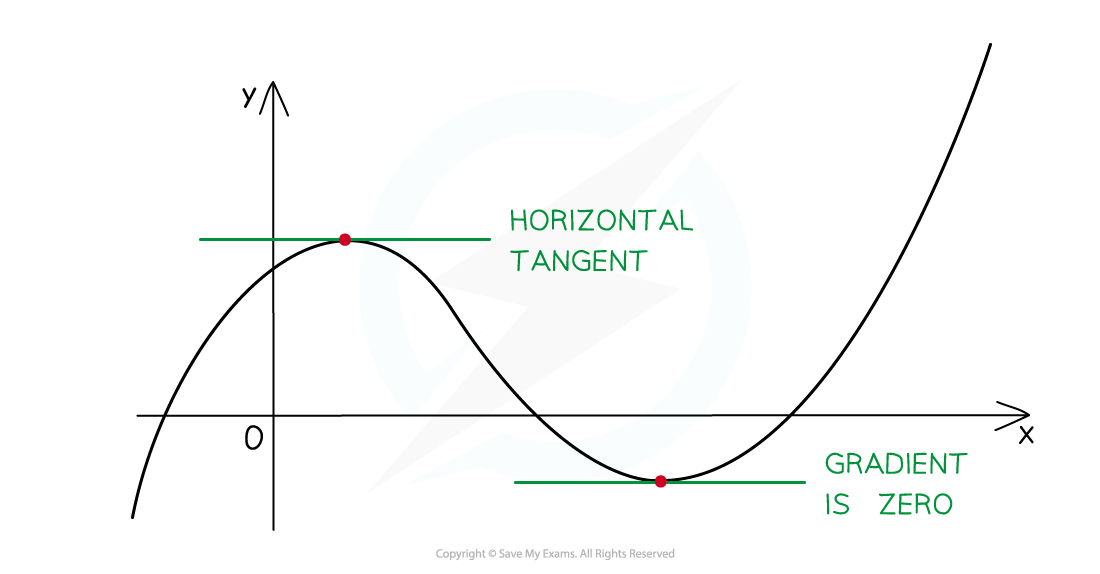
- At a turning point the gradient of the curve is zero
- If a tangent is drawn at a turning point it will be a horizontal line
- Horizontal lines have a gradient of zero
- This means at a turning point the derivative or gradient function equals zero
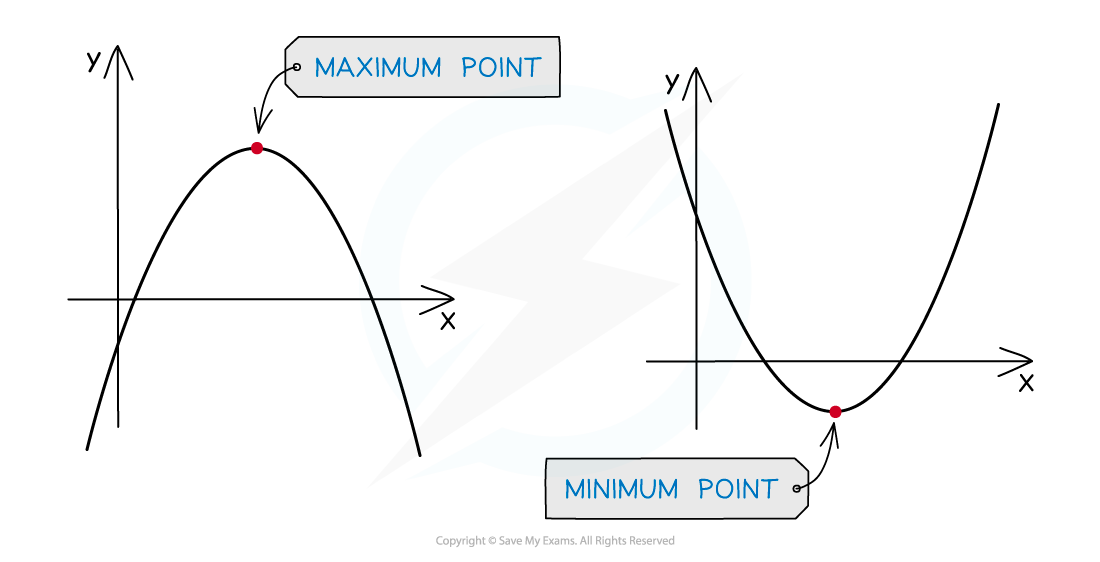
How do I know if a curve has turning points?
- You can see from the shape of a curve whether it has turning points or not
- At IGCSE, two types of turning point are considered:
- Maximum points – this is where the graph reaches a “peak”
- Minimum points – this is where the graph reaches a “trough”
- These are sometimes called local maximum/minimum points as other parts of the graph may still reach higher/lower values
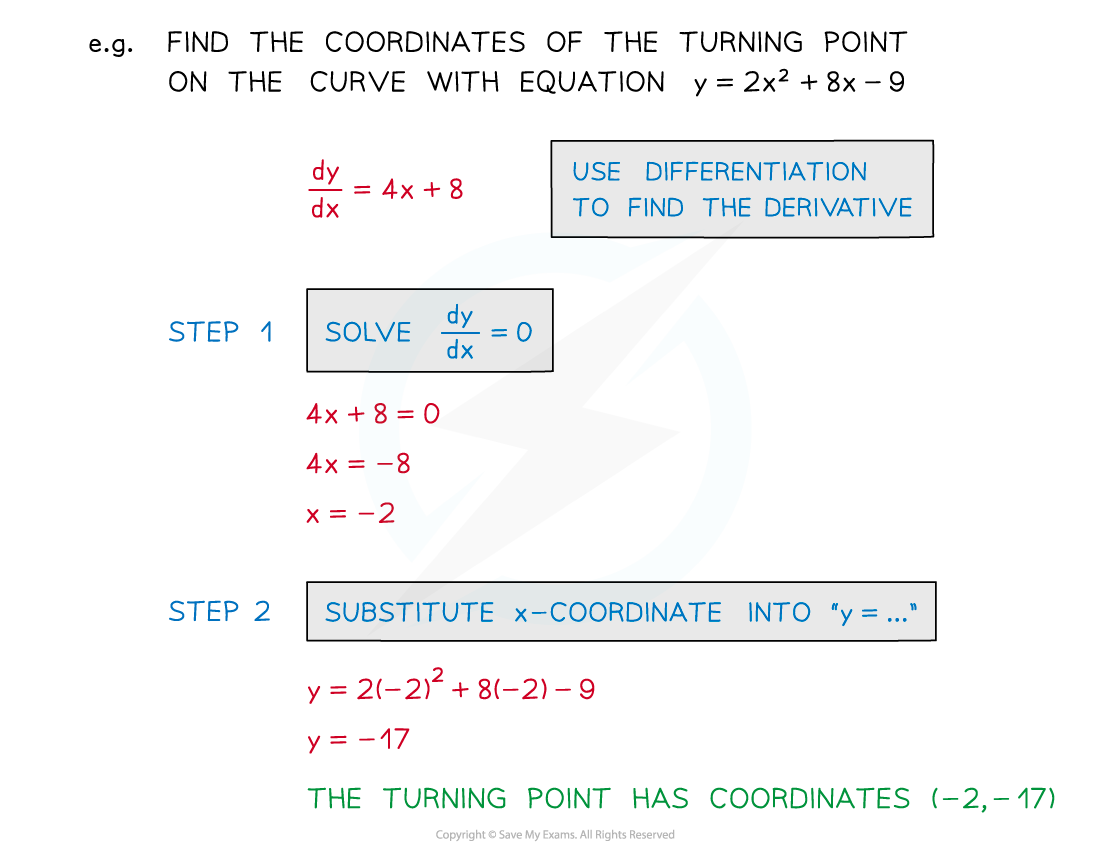
How do I find the coordinates of a turning point?
- STEP 1 Solve the equation of the gradient function (derivative) equal to zeroie. solve dy/dx = 0
This will find the x-coordinate of the turning point
- STEP 2 To find the y-coordinate substitute the x-coordinate into the equation of the graph
ie. substitute x into “y = ...”
How do I know which point is a maximum and which is a minimum?
- The easiest way to do this is to recognise the shape of the curve
- ... either from a given sketch of the curve
- ... a sketch of the curve you can quickly draw yourself
(You may even be asked to do this as part of a question)
- ... the equation of the curve
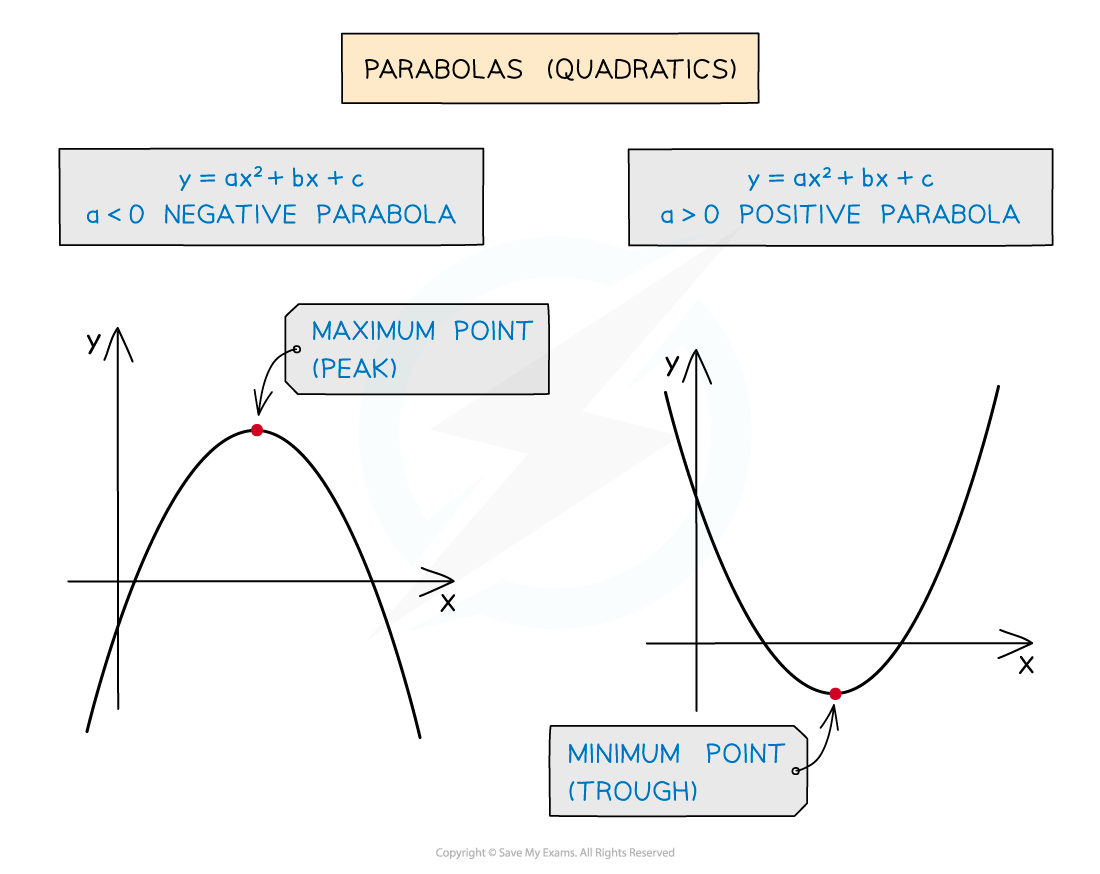
- For parabolas (quadratics) it should be obvious ...
- ... a positive parabola (positive x2 term) has a minimum point
- ... a negative parabola (negative x2 term) has a maximum point
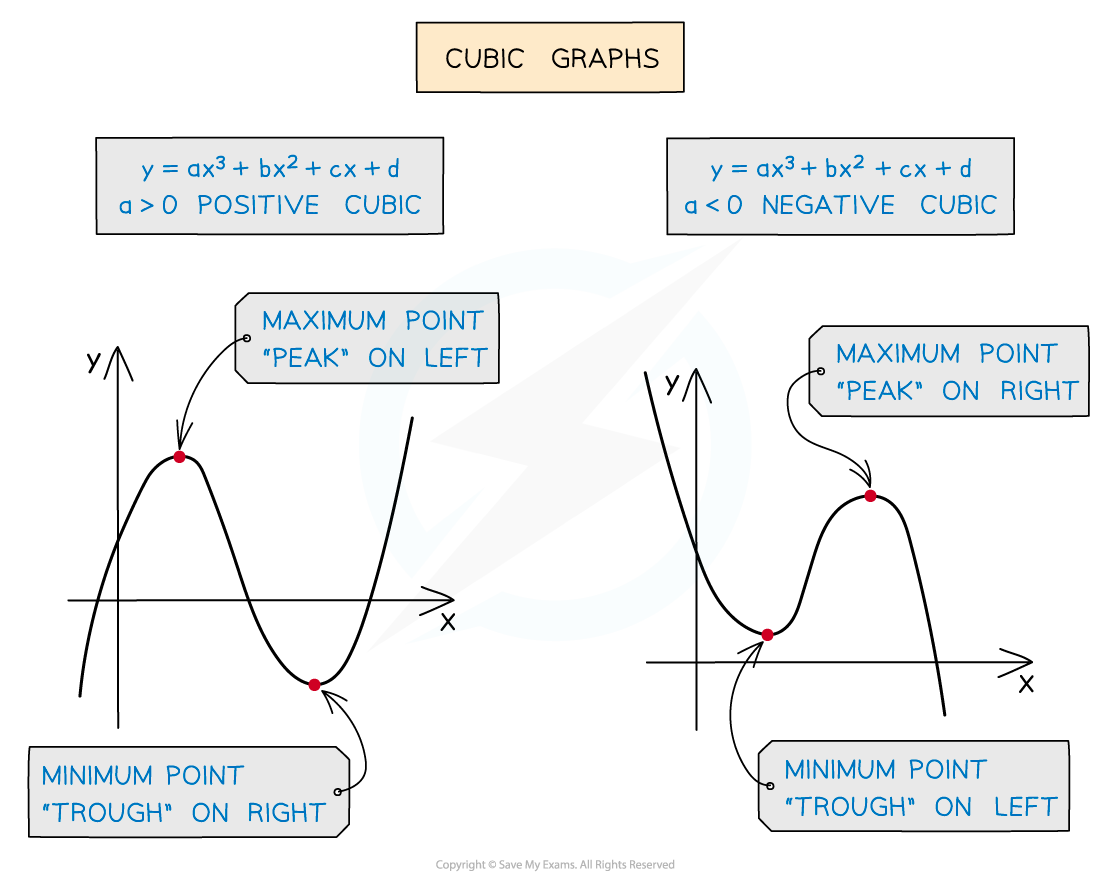
- Cubic graphs are also easily recognisable ...
- ... a positive cubic has a maximum point on the left, minimum on the right
- ... a negative cubic has a minimum on the left, maximum on the right
Exam Tip
Read questions carefully – sometimes only the x-coordinate of a turning point is required.Differentiating accurately is crucial in leading to equations you can work with and solve.
Worked Example
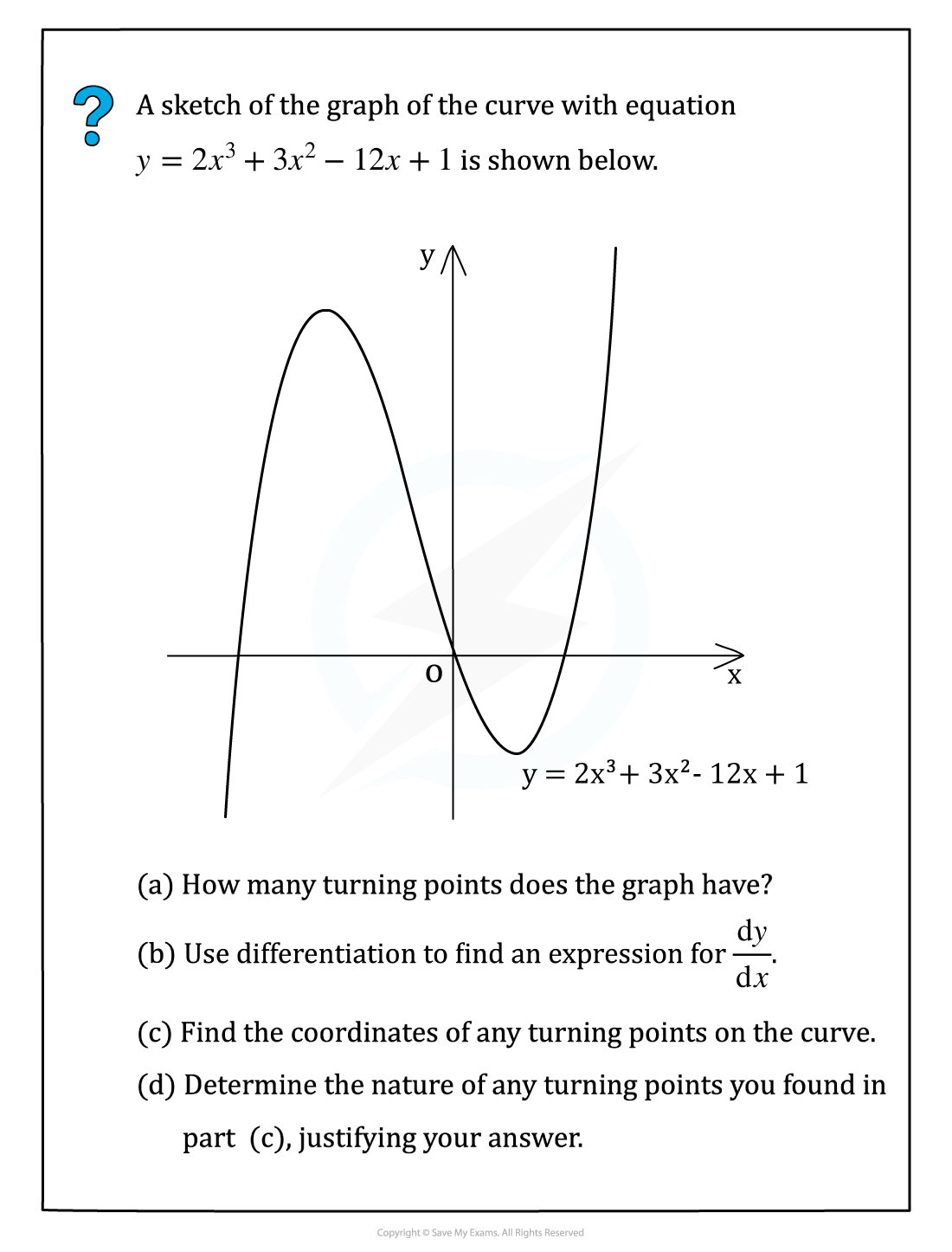
Worked Example

转载自savemyexam
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





